7. Для нахождения sin |
-β- |
и cos -β- воспользуемся формулами сину- |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
са и осинуса половинно$о ар$умента: |
|
|
|
|
|
|
|
sin β = |
1 – cosβ = |
1 – 3-- |
|
|
|
β |
|
1 + cosβ |
|
1 + 3-- |
|
|
-----------4-- |
= |
-----1---- |
- , cos |
= |
= |
-----------4-- |
= ------- |
7--- . |
2 |
2 |
2 |
|
2 |
2 |
2 |
|
2 |
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
8.Подставив найденные значения три$онометричес их фун ций
ввыражение (1), получим
sin |
|
2α – |
β |
= |
4 |
· |
7 |
– |
|
1 |
· |
3 |
= |
4 7 – 3 |
. |
|
2-- |
5-- |
--- |
----- |
---- |
5-- |
--------------- |
------ |
|
|
|
2 |
2 |
|
2 |
|
2 |
|
10 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 4
1.Пусть arccos x = α; то$да 0 < α < π, cos α = x. Нам нужно найти cos 2α.
2.Та а cos 2α = cos2 α – sin2 α, то воспользуемся следующими формулами:
cos (arccos x) = x, $де –1 m x m 1; sin (arccos x) = 
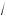 1 – x2 , $де –1 m x m 1.
1 – x2 , $де –1 m x m 1.
3. В результате получим
cos 2α = cos2 α – sin2 α = x2 – (1 – x2) = 2x2 – 1.
К упражнению 4л
1. Та а sin 2α = 2 sin α cos α, то воспользуемся следующими формулами:
|
cos (arctg x) = |
1 |
, sin (arctg x) = |
x |
. |
|
1-----+-----x----2- |
1-----+-----x----2- |
|
|
|
|
|
|
|
|
|
2. То$да получим |
|
|
|
|
|
|
|
|
|
|
sin (2arctg x) = 2sin (arctg x) cos (arctg x) = |
|
|
= 2 · ------------x-------- · |
----------1---------- = |
----- |
2----x------- . |
|
|
|
1 + x |
2 |
1 + x |
2 |
1 |
+ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 5а |
|
|
|
|
|
|
|
|
|
|
1. Перед нами поставлены две задачи: |
|
|
|
|
|
|
а) решить уравнение |
|
|
|
|
|
|
|
|
|
|
sin 4x + cos 3x – sin 2x = 0; |
|
(1) |
|
|
|
|
|
|
|
|
|
|
331 |

б) найти оличество орней это$о уравнения на отрез е |
|
π |
|
3π |
|
. |
|
|
|
-- |
; ------ |
|
4 |
|
4 |
|
|
2. Преобразуем уравнение (1): |
|
|
|
|
|
|
2 sin x cos 3x + cos 3x = 0, или cos 3x(2 sin x + 1) = 0, |
(2) |
3. Левая часть уравнения (2) представляет собой произведение двух множителей. Следовательно, это уравнение распадается на два
уравнения: |
|
|
|
cos 3x = 0, |
(3) |
2 sin x + 1 = 0. |
(4) |
4. Решим уравнение (3). Имеем |
|
|
π |
π k |
, k Ý Z. |
(5) |
x = -- |
+ ------ |
6 |
3 |
|
|
а) Равенство (5) частично отвечает на вопрос о решении данно$о уравнения (1).
б) Теперь нужно выяснить, с оль о орней уравнения (3) принад-
лежит отрез у |
|
π |
3π |
|
. Для это$о запишем неравенство |
|
|
-- |
; ------ |
|
|
|
4 |
4 |
|
|
π |
π |
π k |
3π |
1 |
1 |
k |
3 |
, |
|
т. е. |
1 |
m k m |
7 |
. (6) |
-- |
m -- |
+ ------ |
m ------ , или |
-- |
m -- + -- |
m -- |
|
-- |
-- |
4 |
6 |
3 |
4 |
4 |
6 |
3 |
4 |
|
|
|
|
4 |
|
4 |
|
в) Та а k — целое число, то из двойно$о неравенства (6) следует, |
что k = 1, т. е. уравнение (3) на отрез е |
|
π |
3π |
|
|
имеет один орень. |
|
|
-- |
; ------ |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, от уда |
|
|
|
|
5. Решим уравнение (4). Имеем sin x = – -- |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
(7) |
|
|
|
x = (–1)k + 1 -- + πk, k Ý Z. |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
а) Равенство (7) частично отвечает на вопрос о решении данно$о уравнения (1).
б) Одна о это равенство не позволяет непосредственно выяснить,
с оль о орней уравнения (4) принадлежит отрез у |
|
π |
3π |
|
. |
|
|
|
-- |
; ------ |
|
|
|
4 |
4 |
|
|
в) Чтобы преодолеть возни шее затруднение, перепишем равенст- |
во (7) в виде следующих двух равенств: |
|
|
|
|
|
π |
+ 2πk, k Ý Z; |
|
|
(8) |
x = –-- |
|
|
6 |
|
|
|
|
|
|
5π |
+ 2πk, k Ý Z. |
|
|
(9) |
x = – ------ |
|
|
6 |
|
|
|
|
|
|

$) Та а орни уравнения (7) должны принадлежать отрез у
|
|
π |
3π |
|
, то из равенства (8) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- |
; ------ |
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
π |
|
|
3π |
, |
или |
5 |
11 |
|
|
(10) |
|
|
|
|
|
|
|
-- |
m –-- + 2πk m |
------ |
------ |
m k m ------ . |
|
|
|
|
|
|
|
4 |
6 |
|
|
|
|
4 |
|
|
24 |
24 |
|
|
|
|
|
|
|
|
Неравенство (10) не выполняется ни при а их целых k. |
|
|
|
|
|
|
д) Анало$ично из неравенства (9) следует, что |
|
|
|
|
|
|
|
|
|
|
|
π |
m – |
5π |
|
|
3π |
|
13 |
19 |
|
|
(11) |
|
|
|
|
|
|
|
-- |
------ |
+ 2πk m ------ , или |
------ |
m k m ------ . |
|
|
|
|
|
|
|
4 |
|
6 |
|
|
4 |
|
24 |
24 |
|
|
|
|
|
|
|
|
Неравенство (11) та же не выполняется ни при а их целых k. |
|
|
|
6. Ита , получаем ответ: один орень. |
|
|
|
|
|
|
|
|
|
|
З а м е ч а н и е. Уравнение (4) можно было не решать, пос оль- |
у на отрез е |
|
|
π |
3π |
|
|
|
|
синус положителен и, значит, на этом отрез е |
|
|
|
|
|
|
-- ; ------ |
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение не имеет орней. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем рат ую запись решения данно$о примера: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 3x (2 sin x + 1) = 0; |
|
|
|
|
|
|
а) cos 3x = 0, x = |
π |
π k |
, k Ý Z; |
|
|
|
|
|
|
|
|
|
|
|
-- + ------ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
π |
|
|
|
π k |
m |
3π |
или |
1 |
|
7 |
— один орень; |
|
|
|
|
|
|
|
|
-- m |
-- |
+ ------ |
------ , |
-- |
m k m -- |
|
|
|
|
|
|
4 |
6 |
|
|
|
3 |
|
|
|
|
4 |
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
б) sin x = – |
1 |
|
|
|
|
|
|
π |
+ πk, k Ý Z; |
|
|
|
|
|
|
|
|
|
-- , x = (–1)k + 1 -- |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
на отрез е |
|
|
π |
3π |
|
|
синус положителен — нет орней. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- |
; ------ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 5в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Здесь требуется решить уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ctg x + 2|cos x| = 0 |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
и у азать оличество е$о орней, принадлежащих отрез у |
0; |
|
. |
------ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2.Найдем область определения уравнения (1): sin x − 0, т. е. x − πk,
k Ý Z.
3.Пусть cos x l 0; то$да уравнение (1) примет вид
3 ctg x + 2 cos x = 0, или cos x |
|
3 |
|
= 0. |
(2) |
|
2 + ------------- |
|
|
sin x |
|
|

4. Уравнение (2) распадается на два уравнения: |
|
|
|
cos x = 0, |
(3) |
2 + |
3 |
|
|
|
3 |
(4) |
------------- = 0, |
т. е. sin x = – ------- . |
|
sin x |
|
2 |
|
5. Решив уравнение (3), получим |
|
|
|
π |
|
|
|
|
(5) |
|
x = -- + πk, k Ý Z. |
|
2 |
|
|
|
|
|
6. Найдем оличество орней уравнения (3) на заданном отрез е: |
π |
|
3π |
, |
1 |
|
0 m -- |
+ πk m ------ |
или –-- m k m 1, |
|
2 |
2 |
|
2 |
|
|
|
|
|
3π |
|
|
|
|
т. е. уравнение (3) на отрез е |
0; |
|
|
имеет два орня. |
|
------ |
|
|
|
|
|
|
|
2 |
|
|
|
|
7. Решение уравнения (4) запишем с помощью двух формул: |
|
|
|
π |
|
|
|
|
(6) |
|
x = –-- + 2πk, k Ý Z, |
|
3 |
|
|
|
|
|
|
2π |
+ 2πk, k Ý Z. |
(7) |
|
x = – ------ |
|
3 |
|
|
|
|
|
Серия орней (7) — посторонняя, та а для нее не выполняется условие cos x l 0.
8. Вернемся серии орней (6) и определим оличество орней уравнения (4) на данном отрез е:
π |
|
3π |
|
или |
1 |
|
11 |
|
|
0 m – -- + 2πk m ------ , |
|
-- m k m ------ , |
|
|
3 |
2 |
|
|
|
6 |
|
12 |
|
|
|
|
|
3π |
|
|
|
|
|
|
|
т. е. уравнение (4) на отрез е |
0; |
|
не имеет орней. |
|
|
------ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
9. Пусть теперь cos x < 0; то$да уравнение (1) примет вид |
|
3 ctg x – 2 cos x = 0, |
или cos x |
3 |
– 2 |
= 0. |
(8) |
------------- |
|
|
|
|
|
|
|
sin x |
|
|
|
10. Та а cos x − 0 (со$ласно предположению cos x < 0), то уравнение (8) равносильно следующему:
3 |
– 2 = 0, или sin x |
3 |
(9) |
------------ |
= ------- . |
sinx |
|
|
2 |
|
11. Решение уравнения (9) запишем с помощью двух формул: |
|
|
π |
+ 2πk, k Ý Z; |
|
(10) |
|
x = -- |
|
|
3 |
|
|
|
|
2π |
+ 2πk, k Ý Z. |
|
(11) |
|
x = ------ |
|
|
3 |
|
|
|

Серия орней (10) — посторонняя, пос оль у для нее не выполнено условие cos x < 0.
12. Для серии орней (11) имеем
2π |
|
|
3π |
|
|
|
1 |
5 |
|
|
|
|
|
0 m ------ |
+ 2πk m ------ , или –-- m k m |
------ , |
|
|
|
|
|
3 |
2 |
|
|
|
3 |
12 |
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
т. е. уравнение (9) на отрез е |
0; |
|
имеет один орень. |
|
|
|
|
|
------ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
13. Ита , получаем ответ: три орня. |
|
|
|
|
|
|
К упражнению 6а |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Требуется решить уравнение |
|
|
|
|
|
|
|
|
sin 3x – |sin x| = 0 |
|
|
|
(1) |
и у азать в ответе сумму е$о орней, принадлежащих отрез у |
|
3π |
7π |
|
. |
|
|
------ ; ------ |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
2. Пусть sin x l 0; то$да уравнение (1) примет вид |
|
|
|
|
|
sin 3x – sin x = 0, |
или |
2 sin x cos 2x = 0. |
|
|
(2) |
3. Уравнение (2) распадается на два уравнения: |
|
|
|
|
|
|
|
|
sin x = 0, |
|
|
|
(3) |
|
cos 2x = 0. |
|
|
|
(4) |
4. Решив уравнение (3), получим x = πk, k Ý Z. Чтобы найти оличество е$о орней на заданном отрез е, запишем двойное неравенство
3π |
7π |
, или |
3 |
m k m |
7 |
, |
--4---- |
m πk m ------ |
-- |
4-- |
4 |
|
4 |
|
|
от уда следует, что k = 1. Значит, данное уравнение на отрез е |
|
3π |
; 7π |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
имеет один орень x1 = π. |
|
|
|
|
|
|
|
π |
π k |
, k Ý Z. Для отыс а- |
5. Решив уравнение (4), получим x = -- |
+ ------ |
4 |
2 |
|
|
|
|
|
|
ния оличества е$о орней на у азанном отрез е составим неравенство
3----π-- |
m |
-π- |
+ |
π----k-- |
m |
7----π-- |
, или 1 m k m 3, |
4 |
|
4 |
|
2 |
|
4 |
|
оторое выполняется при k = 1, k = 2 и k = 3. Одна о условию sin x l 0 удовлетворяет толь о значение k = 1, оторому соответствует орень
x2 |
π |
π |
3π |
= -- |
+ -- |
= ------ . |
|
4 |
2 |
4 |
6. Пусть теперь sin x < 0; то$да уравнение (1) примет вид
sin 3x + sin x = 0, |
или |
2 sin 2x cos x = 0. |
(5) |
7. Уравнение (5) распадается на два уравнения: |
|
|
|
sin 2x = 0, |
|
(6) |
|
|
cos x = 0. |
|
(7) |
8. Решив уравнение (6), получим x = |
π k |
|
------ , k Ý Z. Для отыс ания |
|
|
|
|
|
2 |
|
оличества е$о орней на заданном отрез е запишем неравенство |
|
3π |
π k |
7π |
или |
3 |
7 |
|
------ |
m ------ |
m ------ , |
-- |
m k m -- , |
|
4 |
2 |
4 |
|
2 |
2 |
|
оторое выполняется при k = 2 и k = 3. Одна о условию sin x < 0 удовлет-
воряет толь о значение k = 3, оторому соответствует орень x3 |
3π |
= ------ . |
|
|
2 |
π |
+ πk, k Ý Z. Далее запи- |
9. Решив уравнение (7), получим x = -- |
2 |
|
|
шем неравенство
3π |
π |
7π |
1 |
5 |
, |
------ m -- |
+ πk m ------ , или -- |
m k m -- |
4 |
2 |
4 |
2 |
4 |
|
от уда следует, что k = 1. Этому значению k соответствует орень x4 =
= 3π , совпадающий с орнем x . Одна о при записи ответа мы будем
------ 3
2
учитывать этот орень дважды.
10. Найдем сумму орней данно$о уравнения на у азанном отрез е:
3π |
3π |
3π |
19π |
= 855°. |
|
|
x1 + x2 + x3 + x4 = π + ------ |
+ ------ |
+ ------ = |
---------- |
|
|
4 |
2 |
2 |
4 |
|
|
|
|
|
|
К упражнению 6ж |
|
|
|
|
|
|
|
|
|
1. Требуется решить уравнение |
|
|
|
|
|
|
|
|
|
sin 4x + cos 3x – sin 2x = 0 |
|
|
|
|
(1) |
и у азать сумму е$о орней, принадлежащих отрез у |
|
3π |
7π |
|
. |
|
|
------ ; ------ |
|
|
|
|
|
4 |
4 |
|
|
2. Данное уравнение равносильно уравнению |
|
|
|
|
|
|
cos 3x(2sin x + 1) = 0, |
|
|
|
|
|
|
|
оторое в свою очередь равносильно сово упности уравнений |
cos 3x = 0, |
|
|
|
|
|
(2) |
|
1 |
|
|
|
|
|
(3) |
sin x = –-- . |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3. Запишем решение уравнения (2):
|
|
|
π |
+ |
π k |
, k Ý Z. |
|
(4) |
|
|
x = -- |
------ |
|
|
|
|
6 |
|
3 |
|
|
|
|
4. Количество орней уравнения (2) на заданном отрез е опреде- |
лим из неравенства |
|
|
|
|
|
|
|
|
3π |
π |
π k |
m |
7π |
|
или |
7 |
19 |
, |
------ |
m -- |
+ ------ |
------ , |
-- |
m k m ------ |
4 |
6 |
3 |
|
4 |
|
|
4 |
4 |
|
оторое выполняется при k = 2, k = 3 k = 4.
Этим значениям k соответствуют следующие орни:
x1 = |
π |
+ |
2π |
5π |
|
-- |
------ = |
------ = 150° (при k = 2); |
|
|
6 |
|
3 |
6 |
|
x2 = |
π |
+ |
3π |
7π |
|
-- |
------ = |
------ = 210° (при k = 3); |
|
|
6 |
|
3 |
6 |
|
x3 = |
π |
+ |
4π |
3π |
|
-- |
------ = |
------ = 270° (при k = 4). |
|
|
6 |
|
3 |
2 |
|
Та им образом, x1 + x2 + x3 = 630°. |
|
5. Запишем орни уравнения (3) в виде двух равенств: |
|
|
|
|
π |
+ 2πk, k Ý Z; |
(5) |
|
|
x = –-- |
|
|
|
6 |
|
|
|
|
|
5π |
(6) |
|
|
x = – ------ + 2πk, k Ý Z. |
|
|
|
6 |
|
|
6.Используя равенство (5), найдем оличество орней уравнения (3)
взаданном отрез е:
3----π-- |
m –-π- |
|
+ 2πk m 7----π-- , |
или |
11------ m k m |
23------ . |
4 |
6 |
|
|
4 |
|
24 |
24 |
Этому неравенству не удовлетворяет ни одно целое значение k. |
7. Анало$ично, используя равенство (6), имеем |
|
3----π-- |
m –5----π-- |
|
+ 2πk m 7----π-- , |
или |
19------ m k m |
31------ . |
4 |
6 |
|
|
4 |
|
24 |
24 |
Последнему неравенству удовлетворяет значение k = 1, оторому |
соответствует орень x |
4 |
= –5----π-- + 2π = 7----π-- |
= 210°, совпадающий с ор- |
|
|
6 |
6 |
|
|
|
|
|
|
|
|
нем x2.
8. Ита , получаем ответ: x1 + x2 + x3 + x4 = 630° + 210° = 840°.
К упражнению 7а
1. Преобразуем данное уравнение:
sin x – 6 = 3 tg x – 2 cos x; tg x (cos x – 3) = 2(3 – cos x); (cos x – 3)(tg x + 2) = 0.
2.Та а cos x – 3 − 0, то tg x = –2.
3.Нам требуется найти значение выражения 15(sin 2x – cos 2x). Для это$о воспользуемся формулами, выражающими sin 2x и cos 2x через tg x:
sin 2x = -----2-----tg-------x------ , |
cos 2x = -1---- |
-–-----tg------2----x-- , |
1 + tg2 x |
|
|
1 |
+ tg2 x |
от уда находим sin 2x = –4-- , cos 2x = –3-- . |
|
|
|
|
5 |
5 |
|
|
|
|
4. Подставив эти значения в заданное выражение, получим |
15(sin 2x – cos 2x) = 15 – |
4-- |
+ 3-- |
= –3. |
|
|
5 |
5 |
|
К упражнению 8а
1.Требуется решить уравнение 
 3 cos x – cos 2x = 1 и найти сумму е$о орней, удовлетворяющих неравенствам 6 < x < 13.
3 cos x – cos 2x = 1 и найти сумму е$о орней, удовлетворяющих неравенствам 6 < x < 13.
2.Преобразуем данное уравнение:

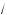 3 cos x – 2 cos x = 1;
3 cos x – 2 cos x = 1; 
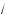 3 cos x = 1 + cos 2x;
3 cos x = 1 + cos 2x;

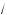 3 cos x = 2 cos2 x, т. е. cos x(
3 cos x = 2 cos2 x, т. е. cos x(
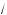 3 – 2 cos x) = 0.
3 – 2 cos x) = 0.
3. Последнее уравнение равносильно следующей сово упности уравнений:
cos x = 0,
cos x = 
 3 .
3 .
-------
2
4. Решением этой сово упности являются числа
π |
+ πk, |
(1) |
|
x = -- |
|
2 |
|
|
|
π |
+ 2πn, |
(2) |
или |
x = -- |
6 |
|
|
|
x = – |
π |
(3) |
|
-- + 2πt, |
|
|
6 |
|
|
x d 3,14 + 3,14k, k Ý Z,
1 -----------
2
x d 3,14 + 6,28n, n Ý Z,
2 -----------
6
x d – 3,14 + 6,28t, t Ý Z.
3 -----------
6
|
|
5. |
Теперь отберем орни, принадлежащие заданному интервалу |
6 < x < 13: |
|
|
|
|
|
|
6 |
< |
3,14 |
+ 3,14k < 13, |
|
|
|
|
|
|
----------- |
|
|
|
|
|
2 |
|
|
1,41 < k < 3,64, |
|
k = 2, k = 3, |
|
6 |
< |
3,14 |
+ 6,28n < 13, или |
|
|
|
|
0,87 < n < 1,98, ^ |
|
n = 1, |
|
----------- |
|
|
|
|
|
6 |
|
|
1,03 < t < 2,15, |
|
t = 2. |
|
|
|
3,14 |
|
|
|
6 |
|
|
|
|
|
|
< –----------- + 6,28t < 13, |
|
|
|
|
|
6 |
|
|
|
|
|
Заметим, что серию орней x = 2πk можно отбросить, та а
эти орни при не оторых значениях k содержатся в серии x = 4π k
----------
3
339
6. Вернемся сериям орней (1), (2), (3) и найдем значения орней в зависимости от k, n, t:
|
|
π |
|
|
|
|
а) для серии (1), т. е. x = -- + πk, имеем |
|
|
|
|
2 |
|
|
|
|
x1 |
π |
+ 2π = |
5π |
(при k = 2); |
|
|
= -- |
------ |
|
|
|
2 |
|
2 |
|
|
|
x2 |
π |
+ 3π = |
7π |
(при k = 3); |
|
|
= -- |
------ |
|
|
|
2 |
|
2 |
|
|
|
|
|
π |
|
|
|
|
б) для серии (2), т. е. x = -- + 2πn, находим |
|
|
|
|
6 |
|
|
|
|
|
π |
+ 2π = |
13π |
(при n = 1); |
|
x3 = -- |
---------- |
|
|
6 |
|
6 |
|
|
|
|
|
π |
|
|
|
|
в) для серии (3), т е. x = – -- + 2πt, получим |
|
|
|
|
6 |
|
|
|
|
|
π |
|
23π |
|
|
x4 = –-- + 4π = ---------- (при t = 2). |
|
|
6 |
6 |
|
|
|
7. Ита , сумма орней, удовлетворяющих заданному неравенст- |
ву, есть x1 + x2 + x3 + x4 = 12π. |
|
|
|
|
К упражнению 8в |
|
|
|
|
|
|
|
|
|
|
5x |
3x |
и найти |
1. Требуется решить уравнение cos x – cos ------ |
= 1 – cos ------ |
|
|
|
|
2 |
2 |
|
оличество е$о орней, удовлетворяющих неравенствам 3 < x < 7. |
2. Преобразуем данное уравнение: |
|
|
|
3x |
|
5x |
|
x |
x |
= 0; |
cos x – 1 + cos ------ – cos |
------ = 0; |
–2 sin2 -- + 2 sin 2x · sin -- |
2 |
|
2 |
|
2 |
2 |
|
2 sin |
x |
sin 2x – sin |
x |
|
= 0; |
x |
· 2 sin |
3x |
5x |
= 0. |
-- |
-- |
2 sin -- |
------ |
cos ------ |
|
2 |
|
|
|
2 |
|
|
2 |
|
4 |
4 |
|
3. Последнее уравнение равносильно сово упности простейших |
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
x |
|
|
|
|
x = 2πk, k Ý Z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- = 0, |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4π k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
3x |
= 0, |
|
|
или |
x = ---------- , k Ý Z, |
|
|
|
|
|
------ |
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2π |
4π k |
|
|
|
|
|
|
|
|
|
|
|
|
, k Ý Z. |
|
|
|
|
cos |
5x |
= 0, |
|
|
|
x = ------ |
+ ---------- |
|
|
|
|
------ |
|
|
|
5 |
5 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(проверьте!). Поэтому последнюю сово упность орней перепишем та :
|
|
4π k |
, k Ý Z, |
|
|
x = ---------- |
|
|
|
3 |
|
|
|
|
2π |
4π k |
|
|
x = ------ + ---------- , k Ý Z. |
|
|
|
5 |
5 |
|
4. Отберем орни уравнения, принадлежащие интервалу (3; 7). |
4π k |
|
4π k |
< 7, |
Для серии орней x = ---------- |
получаем двойное неравенство 3 < ---------- |
3 |
|
|
3 |
|
оторое удовлетворяется толь о при k = 1. Этому значению соответст-
|
|
4π |
вует один орень исходно$о уравнения: x1 = ------ . |
|
|
3 |
2π |
4π k |
|
5. Для серии орней x = ------ + ---------- имеем неравенство |
5 |
5 |
|
2π |
4π k |
< 7, |
3 < ------ |
+ ---------- |
5 |
5 |
|
оторому удовлетворяют два значения k = 1 и k = 2. Им соответствуют
два орня исходно$о уравнения: x = 6π и x = 2π.
2 ------ 3
5
6. Ита , данное уравнение на у азанном интервале имеет три орня.
К упражнению 9а
1. Преобразуем данное уравнение виду sin2 x – 6 sin x + 4a2 – 3 = 0.
2.Пола$ая sin x = z, приходим вадратному уравнению z2 – 6z +
+4a2 – 3 = 0, имеющему орни
z = 3 – 2 |
3 – a2 , |
(1) |
|
1 |
|
|
|
z |
2 |
= 3 + 2 |
3 – a2 . |
(2) |
3.Если D = 3 – a2 l 0, то уравнение (2) не имеет решений, та а z2 = sin x не может быть больше 1.
4.Уравнение (1) имеет решение при условиях
3 – a2 l 0, |
|
3 |
– a2 l 0, |
|
|
|
|
3 – 2 |
3 – a2 |
m 1, |
или |
|
–1 m 3 – 2 3 – a2 m 1, |
|
3 |
– 2 |
3 – a2 |
l –1, |
|
|
|
от уда в результате получаем a2 m 2, т. е. –
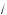 2 m a m
2 m a m 
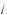 2 .
2 .



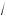 1 – x2 , $де –1 m x m 1.
1 – x2 , $де –1 m x m 1.








 3 cos x – cos 2x = 1 и найти сумму е$о орней, удовлетворяющих неравенствам 6 < x < 13.
3 cos x – cos 2x = 1 и найти сумму е$о орней, удовлетворяющих неравенствам 6 < x < 13.
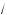 3 cos x – 2 cos x = 1;
3 cos x – 2 cos x = 1; 
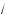 3 cos x = 1 + cos 2x;
3 cos x = 1 + cos 2x;
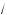 3 cos x = 2 cos
3 cos x = 2 cos
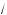 3 – 2 cos x) = 0.
3 – 2 cos x) = 0.


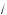 2 m a m
2 m a m 
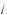 2 .
2 .