Готовимся к экзамену по математике_Крамор В.С_2008 -544с

3. Применение производной к нахождению промежутков монотонности функции

1°. ТЕОРЕМА. Если производная фун ции f в точ е x0 положительна, то фун ция f возрастает в не оторой о рестности этой точ и. Если производная фун ции f в точ е x0 отрицательна, то фун ция f убывает в не оторой о рестности этой точ и.

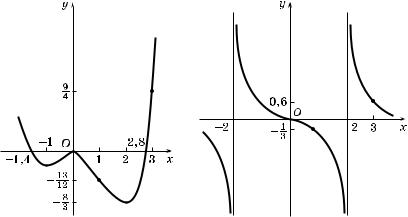
2°. На рис. 181, а и б рафичес и иллюстрируются возрастание и убывание фун ции в зависимости от зна а ее производной в о рестности данной точ и x0. Фун ция, рафи оторой

изображен на рис. 181, а, возрастает в о рестности точ и x0, та а f′(x0) = tg α > 0; фун ция, рафи оторой изображен на рис. 181, б, убывает в о рестности точ и x0, пос оль у f′(x0) = = tg α < 0.

3°. Достаточное условие возрастания (убывания) фун ции на интервале. ТЕОРЕМА. Если фун ция f имеет положительную производную в аждой точ е интервала (a; b), то фун - ция возрастает на этом интервале. Если фун ция f имеет отрицательную производную в аждой точ е интервала (a; b), то фун ция убывает на этом интервале.

4°. Отметим та же, что если фун ция f монотонна на интервале (a; b) и непрерывна в точ ах a и b, то она монотонна и на отрез е [a; b].

Рис. 181

411

Пример. Найти промежут и монотонности фун ции:

а) f(x) = 5x2 – 3x + 1; б) f(x) = 2 .

--

x

Р е ш е н и е. а) Данная фун ция определена на всей числовой прямой. Находим производную: f′(x) = 10x – 3. Та а f′(x) < 0 при x < 0,3 и f′(x) > 0 при x > 0,3, то в промежут е (–×; 0,3] фун ция убывает, а в промежут е [0,3; +×) — возрастает (точ а x = 0,3 в лючается в промежут и монотонности, пос оль у в этой точ е фун ция определена и непрерывна; см. п. 4°).

б) Область определения фун ции — вся числовая прямая за

ис лючением точ и x = 0. Находим f′(x) = – 2 . Очевидно, что

-----

x2

f′(x) < 0 при всех x − 0, т. е. данная фун ция убывает в промежут ах (–×; 0) и (0; +×).

4. Критические точки функции, ее максимумы и минимумы

1°. Внутренние точ и области определения фун ции, в о- торых производная равна нулю или не существует, называют

ритичес ими.

2°. Точ у x0 из области определения фун ции f называют

точ ой миним ма этой фун ции, если найдется та ая δ-о - рестность (x0 – δ; x0 + δ) точ и x0, что для всех x − x0 из этой

о рестности выполняется неравенство f(x) > f(x0).

3°. Точ у x0 из области определения фун ции f называют

точ ой ма сим ма этой фун ции, если найдется та ая δ-о - рестность (x0 – δ; x0 + δ) точ и x0, что для всех x − x0 из этой

о рестности выполняется неравенство f(x) < f(x0).

4°. Точ и минимума и ма симума называют точ ами э с- трем ма данной фун ции, а значения фун ции в этих точ-ах — соответственно миним мом и ма сим мом фун ции (или э стрем мом фун ции).

5°. Фун ция y = f(x), рафи оторой изображен на рис. 182, в точ ах x1 и x3 имеет минимумы (ymin), а в точ ах x2 и x4 — ма симумы (ymax). Заметим, что точ и a и b не считаются точ-ами э стремума фун ции f, та а у аждой из этих точе нет о рестности, цели ом входящей в область определения фун ции.

412

6°. Необходимое условие существования э стремума фун - ции. ТЕОРЕМА ФЕРМА. Если точ а x0 является точ ой э с-

тремума фун ции f(x) и в этой точ е существует производная, то она равна нулю, т. е. f′(x0) = 0.

Например, в точ ах x = –1 и x = 1 фун ция f(x) = 3x – x3 имеет э стремумы (рис. 183) и, следовательно, по теореме Ферма производная в этих точ ах равна нулю: f′(x) = 3 – 3x2; f′(1) = = f′(–1) = 0.

7°. Отметим, что теорема Ферма выражает лишь необходимое условие существования э стремума: из то о, что производная обращается в нуль или не существует в данной точ е x0, не

обязательно следует, что x0 — точ а э стремума.

Та , производная фун ции f(x) =x3 (рис. 184) в точ е x = 0 равна нулю: f′(x) = 3x2; f′(0) = 0. Одна о в этой точ е фун ция не имеет э стремума.

Производная фун ции f(x) = 2x + |x| (рис. 185) в точ е x = 0 не существует. В этой точ е фун ция не имеет э стремума.

413

8°. Достаточные условия существования э стремума. Пусть фун ция f(x) непрерывна в точ е x0 и имеет производную f′(x)

в не оторой о рестности этой точ и. То да:

если f′(x) < 0 на интервале (a; x0) и f′(x0) > 0 на интервале

(x0; b) (т. е. производная меняет зна с минуса на плюс), то x0 —

точ а минимума фун ции f(x);

если f′(x) > 0 на интервале (a; x0) и f′(x0) < 0 на интервале

(x0; b) (т. е. производная меняет зна с плюса на минус), то x0 —

точ а ма симума фун ции f(x).

Пример. Дана фун ция y = 4x2 – 6x. Найти ее ритичес ие точ и, промежут и монотонности, точ и э стремума.

а производная в этой точ е меняет зна с минуса на плюс. Та-

им образом, x = 3 — точ а минимума. Находим значение

--

4

5. Общая схема исследования функции

Общее исследование фун ции и построение ее рафи а ре-омендуется выполнять по следующей схеме.

1.Найти область определения фун ции.

2.Проверить, не является ли фун ция четной или нечетной; проверить та же, не является ли она периодичес ой.

3.Найти, если это возможно, точ и пересечения рафи а фун ции с осями оординат. Ино да для уточнения построения рафи а следует найти две-три дополнительные точ и.

4.Найти производную фун ции и ее ритичес ие точ и.

5.Найти промежут и монотонности и э стремумы фун ции.

414

6. Построить рафи фун ции, используя полученные результаты исследования.

строить ее рафи .

Р е ш е н и е. 1. Здесь D(f) = R.

2.Фун ция не является ни четной, ни нечетной, ни периодичес ой.

3.Найдем точ и пересечения рафи а с осью Ox (т. е. орни фун ции):

Возьмем та же две дополнительные точ и: например, f(1) =

4. Находим производную:

f′(x) = x3 – x2 – 2x = x(x2 – x – 2) = (x + 1)x(x – 2).

Приравняв производную нулю, получим ритичес ие точ-и: x = –1, x = 0, x = 2.

5. Найденные ритичес ие точ и разбивают числовую прямую на четыре промежут а: (–×; –1), (–1; 0), (0; 2) и (2; +×).

Составим таблицу:

В первой стро е таблицы в поряд е возрастания расположены ритичес ие точ и фун ции и о раниченные ими промежут и; во второй — отмечены зна и производной в этих промежут ах. В третьей стро е сделаны выводы об изменении фун ции и хара тере ее ритичес их точе , а та же вычислены значения фун ции в точ ах э стремума.

415

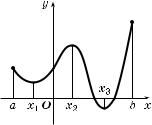
6. Используя результаты исследования, строим рафи фун ции (рис. 186).

Р е ш е н и е. 1. Фун ция определена при всех значениях x,роме x = –2 и x = 2, т. е. D(f) = (–×; –2) (–2; 2) (2; +×). Отметим, что y º 0 при x º +× и при x º –×; роме то о, y º ä× при x º 2 и x º –2.

2.Фун ция является нечетной, та а f(–x) = –f(x). Следовательно, ее рафи симметричен относительно начала оординат и достаточно исследовать фун цию лишь на промежут е [0; +×).

3.Если x = 0, то y = 0, т. е. точ а (0; 0) принадлежит рафи-у фун ции. Возьмем та же две дополнительные точ и: на-

пример, f(1) = –1 , f(3) = 0,6.

--

3

4. Находим производную:

5.Очевидно, что f′(x) < 0 при всех значениях x Ý D(f). Следовательно, фун ция убывает на промежут ах (–×; –2), (–2; 2)

и(2; +×). Э стремумов фун ция не имеет.

6.На основании полученных сведений строим рафи фун - ции (рис. 187).

416

6. Задачи на отыскание наименьшего и наибольшего значений функции

1°. На рис. 188 изображен рафи не оторой фун ции f, определенной на отрез е [a; b]. В точ е x2 фун ция имеет ма си-

мум, а в точ ах x1 и x3 — минимумы. Свое о наименьше о зна-

чения, а это видно из рисун а, фун ция дости ает в точ е x3 — точ е наименьше о из минимумов. Наибольшее значение

фун ция принимает на онце отрез а в точ е b, в оторой фун ция не имеет э стремума (та а справа от точ и b фун - ция не определена).

2°. Для отыс ания наименьше о и наибольше о значений фун ции,

дифференцируемой в данном промежут е, следует найти все ритиче- с ие точ и фун ции, лежащие внутри промежут а, вычислить значе-

ния фун ции в этих точ ах и наонцах промежут а, а затем из всех

полученных та им образом чисел выбрать наименьшее и наибольшее.

Примеры. 1. Найти наименьшее и наибольшее значения фун ции y(x) = –2x3 – 3x2 + 4 в промежут е: а) [–2; –0,5]; б) [1; 3).

Р е ш е н и е. Находим ритичес ие точ и фун ции. Таа y′(x) = –6x2 – 6x = –6x(x + 1), то имеются две ритичес ие точ и: x = 0 и x = –1.

а) В промежут е [–2; –0,5] лежит одна из ритичес их точе : x = –1. Та а y(–2) = 8, y(–1) = 3, y(–0,5) = 3,5, то наименьшее значение фун ции y(x) = –2x3 – 3x2 + 4 дости ается в точ е x = –1 и равно 3, а наибольшее — в точ е x = –2 и равно 8. Крат о это можно записать та :

б) В промежут е [1; 3) данная фун ция убывает. Поэтому max y(x) = y(1) = –1. Наименьше о значения в промежут е [1; 3)

[1; 3]

фун ция не дости ает, та а точ а x = 3 не принадлежит этому промежут у.

417

2. Вписать в ру радиуса R прямоу ольни наибольшей площади.

Р е ш е н и е. Обозначим длину одной из сторон прямоу ольни а через x (рис. 189);

то да длина дру ой стороны равна 4R2 – x2 .

Заметим, что 0 m x m 2R, та а 4R2 – x2 l 0. Значит, площадь прямоу ольни а выразится

Рис. 189

равенством S(x) = x 4R2 – x2 .

Найдем наибольшее значение фун ции S(x) на отрез е [0; 2R]. Имеем S′(x) = 0, т. е.

от уда x = R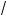2 (значение x = –R2 , очевидно, не удовлетворяет условию.) Следовательно, надо сравнить значения фун -

ции при x = R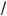2 (в точ е э стремума), x = 0 и x = 2R (на онцах отрез а). Та а S(0) = S(2R) = 0, а S(R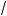2 ) = 2R2, то фун ция принимает наибольшее значение при x = R2 . То да длина дру ой стороны прямоу ольни а равна 4R2 – x2 = = R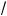2 , т. е. ис омым прямоу ольни ом служит вадрат.

КОНТРОЛЬНЫЕ ВОПРОСЫ

418

УПРАЖНЕНИЯ

1. Через данную точ у A проведена асательная у азанной ривой y = f(x). Найдите оординаты точ и асания, если:

а) A(9; 2), y = 17 – x2 ; б) A(–5; 1), y = –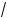13 – x2 ;

в) A(7; 1), y = 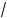10 – x2 .

2. К рафи у данной фун ции f(x) проведена асательная в точ е с у азанной абсциссой x0. Найдите расстояние от начала

оординат до этой асательной, если:

3. Установите, при а ом значении k данная прямая является асательной у азанной параболе, если прямая и парабола заданы соответственно уравнением:

а) y = kx + 5, y = x2 – 4x – k; б) y = kx – 3, y = k – 2x – x2; в) y = kx + 7, y = x2 + 6x + k.

419

вточ е ее пересечения с осью ординат.

5.Составьте уравнение та ой асательной заданнойривой y = y(x), оторая проходит через у азанную точ у, если:

а) y = 1 – x , A(1; –1);

-------------

x

б) y = x2 – 1 , B(–0,75; 1);

----------------

x2

в) y = x – 1 – x2 , C(0; –3).

--------------------------

x

В ответе у ажите сумму оординат точ и асания.

6. Найдите значение k, при отором асательная у азанной ривой y в точ е с заданной абсциссой x0 является одно-

временно и асательной заданной параболе ϕ(x), если: а) y = 3x2 + 5x + 4, ϕ(x) = 5x2 – 7x + k, x0 = 0;

б) y = x2 – 3x + 2, ϕ(x) = 2x2 – 13x + k, x0 = 2; в) y = 3 + 2x – x3, ϕ(x) = x2 – 6x + k, x0 = –2. 7. Найдите ординату точ и на ривой:

а) y = x3 – x2 – 16x + 5, если в этой точ е асательная параллельна прямой y + 11x – 4 = 0, а абсцисса точ и является целым числом;

лельна прямой 3x – 12y – 12 = 0, а абсцисса точ и положительна;

в) y = 29x – 13x2 – x3, если в этой точ е асательная параллельна прямой y + 35x = 4, а абсцисса точ и положительна.

8. Найдите площадь треу ольни а, образованно о осямиоординат и асательной, проведенной рафи у фун ции:

420