
13. При а их значениях параметра a система уравнений
6 · 2x2 + 2 = 4a – sin y,  5 sin y + 10 = a + 23 + x2
5 sin y + 10 = a + 23 + x2
несовместна?
Задания для повторения
14. Имеются два слит а сплавов золота и меди. В первом слит-е отношение золота меди равно 1 : 2, а во втором — 2 : 3. Если
сплавить |
1 |
перво о слит а с |
5 |
второ о слит а, то в получен- |
-- |
-- |
|
3 |
|
6 |
|
ном слит е о ажется столь о золота, с оль о было меди в пер-
вом, а если |
2 |
перво о слит а сплавить с |
1 |
второ о, то в полу- |
-- |
-- |
|
3 |
|
2 |
|
ченном слит е о ажется меди на 1 больше, чем было золота во втором слит е. С оль о золота в аждом слит е?
15.Проценты содержания (по массе) спирта в трех растворах образуют еометричес ую про рессию. Если смешать первый, второй и третий растворы в новом отношении 2 : 3 : 4, то получится раствор, содержащий 32% спирта. Если же смешать их в отношении 3 : 2 : 1, то получится раствор, содержащий 22% спирта. С оль о процентов спирта содержит первый раствор?
16.Сравните числа:
а) a = 4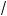 11 и b = 3
11 и b = 3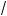 5 ; б) a =
5 ; б) a = 
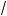 7 +
7 + 
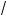 10 и b =
10 и b = 
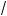 6 +
6 + 
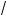 11 .
11 .
17.Сумма атетов прямоу ольно о треу ольни а равна 14 см, ипотенуза равна 10 см. Найдите произведение синусов острых у лов треу ольни а.
18.Один из атетов прямоу ольно о треу ольни а втрое больше дру о о. Найдите отношение суммы синусов острых у - лов треу ольни а разности синусов этих у лов.
19.Найдите множество значений фун ции y = sin 2x, если:
а) x Ý |
|
5 |
5π |
|
; б) x Ý [arctg 0,5; arctg 3]. |
|
|
|
arccos ------ ; ------ |
|
|
|
13 |
12 |
|
|
20. При а их значениях a имеют общий орень уравнения: а) x2 – (a + 3)x + 2a + 2 = 0 и x2 + (a + 3)x + 4a – 4 = 0; б) x2 – (a + 5)x + a + 4 = 0 и x2 + (a – 2)x + 3a – 15 = 0? В ответе у ажите сумму найденных значений a.
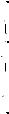
21. При а их значениях x являются последовательными числами еометричес ой про рессии заданные числа:
а) 5 · 4–x; 1 – 4–x; 1 + 29 · 4–x; б) 1 + 137 · 5x; 1 – 7 · 5x; 2 · 5x?
22. При а их значениях k имеет хотя бы одно решение система:
а) 
 x2 – 2kx + k2 – 1 = 0,
x2 – 2kx + k2 – 1 = 0,  |x + 1| m 2;
|x + 1| m 2;
б) 
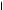 x2 – 2(k – 1)x + k2 – 2k = 0,
x2 – 2(k – 1)x + k2 – 2k = 0,  |x – 2| m 3;
|x – 2| m 3;
в) |
|
|
x2 – 2(k + 2)x + k2 + 4k + 3 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|x – 2| m 1? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. Найдите сумму орней уравнения: |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) (2x |
|
– 12x + 13) |
log3 -3- |
= 3 log3 -3- ; |
|
|
|
|
б) (x |
2 |
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– 4x + 9)log5 -5- = 3 |
|
log5 5-- |
|
; |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) (2x |
|
– 16x + 27) |
log4 4-- |
= 3 log4 -4- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О Т В Е Т Ы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
π |
+ πk, k |
|
π |
+ πk, |
1. а) x = 2πk, x = -- |
+ 2πk, k Ý Z; б) –-- |
Ý Z; в) x = -- |
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
π k |
|
x = –arctg 3 + πk, k Ý Z; $) x = πk, k Ý Z; д) x = ------ |
+ ------ , k Ý Z; е) x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
6 |
|
|
π |
|
|
|
|
|
|
|
|
π |
π k |
7π |
π k |
|
|
π |
= –-- |
+ 2πk, k Ý Z; ж) x = –------ |
+ ------ , x = |
------ + ------ |
, k Ý Z; з) x = -- + |
2 |
|
|
|
|
|
|
|
96 |
|
|
8 |
|
|
36 |
3 |
|
|
4 |
π k |
, k |
|
|
|
π |
|
π k |
|
|
|
|
|
|
π |
+ πk, |
+ ------ |
Ý Z; и) x = -- |
+ ------ , k Ý Z. 2. а) Нет орней; б) x = ä-- |
2 |
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
= ä |
π |
|
k Ý Z; в) x = πk, k Ý Z; $) x = ä-- + πk, k Ý Z; д) x |
-- + πk, k Ý Z; |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
π |
+ πk, |
е) нет орней; ж) нет орней; з) нет орней; и) x = ä-- + |
πk, x = -- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
1 |
|
k Ý Z; ) x = -- + πk, k |
Ý Z. 3. а) x = -- + πk, x = –arctg |
-- + πk, k Ý Z; |
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
1 |
+ πk, |
б) x = -- |
+ πk, x = –arctg 3 + πk, k Ý Z; в) x = –-- |
+ πk, x = arctg -- |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
5 |
k Ý Z; $) x = -- + πk, x = –arctg 2 + πk, k Ý Z; д) x = -- |
+ πk, x = arctg -- + |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
3 |
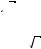
+ πk, k Ý Z; е) x = -π- |
|
+ πk, x = -π- |
|
+ πk, k Ý Z; ж) x = πk, x = |
-π- |
+ πk, |
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
k Ý Z; з) x = |
-π- + πk, x = |
|
-π- |
+ πk, k Ý Z; и) x = πk, x = |
|
-π- |
+ πk, k Ý Z; |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
) нет орней. 4. а) 14 орней; б) 14 орней. 5. а) -π- ; б) |
-π- |
. 6. а) 5760; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
б) 5000. 7. а) x = (–1) |
k π |
+ |
πk; x = – |
π |
+ πk, x |
= –arctg |
47 |
+ πk, k Ý Z; |
|
-- |
-- |
- |
---- |
- |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
б) x = -π- + 2πk, x = |
--π---- |
|
+ |
|
2-- arctg |
40------ |
+ |
2- π k--------- , k Ý Z; в) x = |
-π- + |
π----k-- , x = |
|
|
|
2 |
|
|
|
14 |
|
|
7 |
|
9 |
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
4 |
|
|
|
= |
--π---- |
|
+ π----k-- |
, x = --π---- |
+ |
π----k-- |
, k Ý Z; $) x = |
-π- |
+ πk, x = - |
-π---- + |
π----k-- |
, x = -- |
π---- |
+ |
π----k-- , |
|
24 |
12 |
|
12 |
|
|
6 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
26 |
13 |
|
12 |
|
6 |
k Ý Z. 8. а) x = -π- |
+ πk, y = –7----π-- + πk, k Ý Z; б) x = 1-- |
(q + πk + (–1)k × |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
× arcsin(2p – sin q)), y = |
1-- |
(q – – πk – (–1)karcsin(2p – sin q)), k Ý Z, $де |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|2p – sin q| m 1; в) x = |
|
q |
+ πk ä ä |
1 |
arccos |
2 sinq |
– cos q |
|
, y = |
q |
– πk å |
|
2-- |
2-- |
--- |
----p---- |
---- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
å |
1 |
arccos |
2 sinq |
– cos q |
|
, k Ý Z, $де |
|
2 sinq |
– cos q |
|
m 1; $) x = |
π |
+ |
|
|
2-- |
---- |
---p-------- |
|
|
----- |
-- |
p----- |
--- |
|
3-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ π(n + k), y = π + π(n – k); x = –π-- -- |
+ π(n + k), y = – π + π(n – k), n, k Ý Z;-- |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
д) x = –-π- + π----k-- , y = 7----π-- |
– π----k-- |
, k Ý Z; е) x = – |
-π- |
+ |
π----n-- |
– πk, y = |
-π- + |
π----n-- |
+ πk, |
|
|
|
8 |
2 |
8 |
|
|
2 |
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
4 |
2 |
|
|
|
n, k Ý Z. 9. а) 5 и –5; б) 5 и 0; в) 13 и –13; $) 30 и –20; д) 4 2 |
и 0; |
е) наибольшее значение не существует; наименьшее значение равно |
---1--- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
10. а) –-π- + 2πk < x < 7----π-- |
+ 2πk, k Ý Z; б) –2π------ |
+ 2πk < x < 2----π-- |
+ 2πk, k Ý Z; |
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
в) 4-----π- |
+ 4πk < x < |
14--------π-- |
+ 4πk, k Ý Z; $) |
- |
-π---- |
|
+ πk < x < |
11--------π-- |
+ πk, k Ý Z; |
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
д) – |
-π- |
+ πk < x < -π- |
+ πk, k Ý Z; е) πk < x < |
5----π-- |
+ πk, k Ý Z; ж) -π- |
+ |
π----k-- |
< |
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
3 |
|
< x < |
-π- + |
π----k-- |
, k Ý Z; з) |
-π- |
|
+ 2πk < x < 2π + 2πk; и) –-π- + 2πk < x < |
7----π-- |
+ |
|
|
|
4 |
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
6 |
|
+ 2πk, k Ý Z; ) –-π- |
+ πn < x < –-π- |
+ πn, – |
-π- |
+ πn < x < |
|
-π- |
+ πn, n Ý Z; |
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
л) πk < x < -π- |
+ πk, πk – |
-π- |
+ 1-- arcsin |
2-- |
|
m x m –1 arcsin-- |
2-- |
+ πk. k Ý Z; |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
м) если a m –1, то решений нет; если –1 < a m 1, то arccos a + 2πk < x < < 2π – arccos a + 2πk, k Ý Z; если a > 1, то x Ý R; н) πk < x m arcctg a + πk,
363

k Ý Z. 11. а) |
1 |
|
1 |
1 |
. 12. |
а) 3; б) 0; в) 1. 13. –× < a < 2, |
-- |
; б) –-- ; в) 1; $) 1; д) -- |
|
2 |
|
2 |
2 |
|
|
3 < a < +×. 14. 1,2 $; 2,4 $. 15. 12%. |
12 |
16. а) a > b; б) a > b. 17. ------ . |
|
|
|
|
|
|
|
|
25 |
18. 2. 19. а) |
|
|
1 |
120 |
|
; б) [0,6; 1]. |
20. |
а) –6; б) –2,5. 21. а) 2; б) –2. |
|
|
|
|
|
-- ; |
--------- |
|
|
|
|
2 |
169 |
|
|
|
|
22. а) –4 m k m 2; б) –1 m k m 7; в) –2 m k m 2. 23. а) 10; б) 18; в) 13.
Решения и методичес ие у азания
Ниже даны решения различных видов уравнений. При решенииаждо$о из этих уравнений используется тот или иной способ (часто одно и то же уравнение можно решить разными способами). Мы проиллюстрируем эти способы в процессе решения заданных уравнений.
К упражнению 1а
1.Положим y = sin x + cos x; то$да (sin x + cos x)2 = y2, или y2 =
=1 + sin 2x.
2.Следовательно, данное уравнение примет вид
|
y2 – 1 – 4y + 4 = 0, т. е. y2 – 4y + 3 = 0, |
|
|
|
от уда находим y1 = 1, y2 = 3. |
|
|
|
|
|
|
|
|
3. |
Теперь задача сводится решению сово упности уравнений: |
|
sin x + cos x = 1; |
sin x + cos x = 3. |
|
|
|
|
4. |
Та а |
|
|
|
|
|
|
|
|
|
|
|
|
sin x + cos x = |
2 |
|
2 |
2 |
|
= |
2 cos |
π |
– x |
|
, |
|
|
------ sin x |
+ ------ cos x |
|
-- |
|
|
|
|
2 |
2 |
|
|
4 |
|
|
то получаем следующую сово упность уравнений:
|
2 cos |
|
π |
– x |
= 1, |
или |
cos |
|
π |
– x |
1 |
; |
(1) |
|
-- |
-- |
= ------ |
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos |
π |
– x |
|
= 3, |
или |
cos |
π |
– x |
|
3 |
|
(2) |
|
|
-- |
|
|
-- |
|
= ------ . |
|
|
4 |
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Уравнение (1) имеет решения |
|
|
|
|
|
|
|
|
π |
|
π |
+ 2πk и |
π |
|
π |
+ 2πk, k Ý Z, |
|
-- |
– x = -- |
-- – x = – |
-- |
|
4 |
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
π |
+ 2πk, k Ý Z. |
|
|
|
|
|
|
|
|
|
т. е. x = 2πk и x = -- |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

6. Уравнение (2) не имеет решений, пос оль у 3 > 1.
------
 2
2
Ответ: x = 2πk, x = π + 2πk, k Ý Z.
--
2
К упражнению 1в
1. Та а sin 2x = 2 sin x cos x, а 1 + cos 2x = 2cos2 x, то данное уравнение примет вид
6 sin x cos x + 2 cos2 x = 0, или 2 cos x (3 sin x + cos x) = 0.
2. Теперь задача сводится решению сово упности уравнений:
cos x = 0; 3 sin x + cos x = 0.
3. Первое из этих уравнений имеет решения
x = π + πk, k Ý Z.
--
2
4. Второе уравнение является однородным. Разделив обе е$о части на sin x (та а sin x − 0), получим
ctg x = –3, или x = –arcctg 3 + πk, k Ý Z.
З а м е ч а н и е. Данное уравнение можно решить дру$им способом, если воспользоваться универсальной три$онометричес ой подстанов ой tg x = t. То$да
sin 2x = -----2-----tg-------x------ |
= -----2----t------ |
, |
cos 2x = -1-----–-----tg------2----x-- |
= -1-----–-----t---2- . |
1 + tg2 x |
1 + t2 |
|
1 + tg2 x |
1 + t2 |
В результате исходное уравнение сведется ал$ебраичес ому уравнению относительно переменной t = tg x.
К упражнению 1
1. Используя известное тождество a4 + b4 = (a2 + b2)2 – 2a2b2, запишем данное уравнение в виде
sin2 |
x |
+ cos2 |
x |
|
2 |
– 2 sin2 |
x |
cos2 |
x |
5 |
(1) |
-- |
-- |
|
-- |
-- |
= -- . |
|
3 |
|
3 |
|
|
|
3 |
|
3 |
8 |
|
2. После преобразования уравнения (1) получим
1 – 1-- --sin2 2--x-- = 5-- |
; |
sin2 2----x-- = 3-- |
; |
sin 2----x-- = ä--- |
--3-- . |
(2) |
2 |
3 |
8 |
|
3 |
4 |
|
3 |
2 |
|
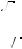
3. |
Решим уравнение (2): |
|
|
|
|
|
|
|
|
|
|
|
2x |
3 |
|
3 |
–1 |
k |
π |
|
|
; |
а) sin ------ |
= ------- , |
|
т. е. x = -- |
|
|
|
-- + πk |
|
|
3 |
2 |
|
2 |
|
|
|
3 |
|
|
|
2x |
3 |
, |
т. е. x = |
3 |
|
–1 |
|
k + 1 π |
+ πk . |
б) sin ------ |
= –------- |
-- |
-- |
|
3 |
2 |
|
|
2 |
|
|
|
|
3 |
|
|
|
4. |
Объединив полученные орни, находим |
|
|
|
|
|
π |
+ |
3π k |
, k Ý Z. |
|
|
|
|
|
x = ä-- |
---------- |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
5. |
Последнее выражение можно упростить: |
x= πk, n Ý Z.
За м е ч а н и е. Это уравнение можно решить дру$им способом, если воспользоваться формулами понижения степени:
|
sin2 α = 1-----–--------cos--------2---α--- |
; |
cos2 |
α = 1------+-------cos--------2----α-- . |
|
|
|
2 |
|
|
|
|
|
|
2 |
То$да данное уравнение примет вид |
|
|
|
|
|
|
2x 2 |
|
|
|
2x 2 |
|
|
|
|
1 – cos |
---3--- |
|
1 + cos---3--- |
|
= |
5 |
и т. д. |
|
-------------2-------- |
------ |
+ |
------ |
------- |
2-------------- |
|
8-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 1д |
|
|
1. Найдем ОДЗ уравнения: |
|
|
π |
π k |
, k Ý Z. |
cos 3x − 0, т. е. x − -- |
+ ------ |
6 |
3 |
|
2. Та а cos2 3x – sin2 3x = cos 6x, то данное уравнение можно переписать в виде
cos 6x – tg2 3x + 1 = 0.
3. Выразив cos 6x через tg 3x и используя подстанов у tg2 3x = y, получим
1 – tg2 3x |
– tg |
2 |
3x + 1 = 0, или |
1 – y |
– y + 1 = 0. |
--------------------------- |
|
------------- |
1 + tg2 3x |
|
|
|
1 + y |
|
Это уравнение имеет орни y1 = –2 и y2 = 1.
4.Ясно, что уравнение tg2 3x = –2 не имеет решений.
5.Остается решить уравнение tg2 3x = 1, т. е. tg 3x = ä1. Имеем:
а) tg 3x = –1, x = – π + π k , k Ý Z;
------ ------
12 3
б) tg 3x = 1, x = π + π k , k Ý Z.
------ ------
12 3
З а м е ч а н и е. Это уравнение можно решить дру$им способом. Та а
cos |
2 |
3x – sin |
2 |
3x = cos 6x, |
|
2 |
|
cos2 3x – sin2 3x |
= |
cos 6x |
, |
|
|
1 – tg |
3x = |
--- |
---- |
------ |
-cos---------2---3----x------ |
--------- |
- cos - - - - - - - - - 2 - - - |
3----x-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то после преобразований уравнение примет вид |
|
|
|
|
|
|
|
|
|
|
cos 6x + -- |
cos----------6----x--- |
= cos 6x 1 + |
--- |
------ |
1-------- |
-- |
= 0. |
|
|
|
|
|
|
|
|
|
|
cos2 3x |
|
|
|
|
|
cos2 3x |
|
|
|
|
|
|
Далее имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) cos 6x = 0, 6x = -π- |
+ πk, от уда x = |
-- |
π---- |
|
+ |
π----k-- , k Ý Z; |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
12 |
|
6 |
|
|
|
|
|
|
|
б) 1 + |
|
= 0 — это уравнение не имеет решений. |
|
|
|
|
- cos - - - - - - - - - 2 - - - 3 - - --x-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: x = - |
-π---- |
+ π----k-- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 1е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Найдем ОДЗ уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x-- |
− 0, т. е. x − π + 2πk, k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Положив tg x-- |
= y и выразив cos x через tg x-- , получим |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 – tg |
2 x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
-- |
– 2tg x |
|
|
|
|
–2 + 1 |
– y |
|
|
|
|
|
|
|
–2 ------ -+ |
--- |
------- |
-----2-- |
= 0, |
или |
|
-- |
– 2y = 0. |
|
(1) |
|
|
|
|
|
2 x |
|
2 |
|
|
|
|
|
|
|
1 |
+ y |
2 |
|
|
|
|
|
|
|
|
1 + tg |
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. После упрощения уравнения (1) придем убичес ому уравне- |
нию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2y3 + 3y2 + 2y + 1 = 0. |
|
|
|
|
|
|
|
(2) |
4. Заменим одночлен 3y2 суммой одночленов 2y2 + y2, то$да в ле- |
вой части уравнения (2) получим произведение двух множителей: |
|
|
|
|
|
|
|
|
(y + 1)(2y2 + y + 1) = 0. |
|
|
|
|
|
|
|
Далее имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) y = –1, tg |
x |
|
|
x |
π |
+ πk, x = – |
π |
+ 2πk, k |
Ý Z; |
|
|
|
2-- |
= –1, -- = – |
4-- |
2-- |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) уравнение 2y2 + y + 1 = 0 не имеет решений, та а D < 0. |
|
Ответ: x = – |
-π- |
+ 2πk, k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

З а м е ч а н и е. Это уравнение можно решить иначе, например та :
–2 – 2tg |
x |
+ cos x = 0; –2 |
|
1 + tg |
x |
+ cos |
2 x |
– sin |
2 x |
= 0; |
-2- |
|
-2- |
-- |
-- |
|
|
|
|
2 |
|
2 |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
cos |
-2- + sin |
2-- |
|
+ |
|
cos |
x |
+ sin |
x |
cos |
x |
– sin |
x |
= 0; |
|
---------- |
-cos----------x---------- |
-- |
|
|
2-- |
-2- |
2-- |
-2- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
x |
+ sin |
x |
|
–2 |
+ cos |
x |
– sin |
x |
= 0 и т. д. |
|
|
-2- |
2-- |
|
- cos---------x--- |
2-- |
-2- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
К упражнению 1ж
1. Преобразуем два последних сла$аемых следующим образом:
|
3 sin 5x + cos 5x = 2 |
|
|
3 |
sin 5x + |
1 |
cos 5x |
|
= |
|
|
|
|
---2---- |
-2- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
cos |
π |
sin 5x + sin |
π |
|
cos 5x |
|
= 2sin |
|
5x |
+ |
π |
|
. |
|
|
|
|
6 |
|
|
|
|
|
6-- |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
2. То$да данное уравнение примет вид |
|
|
|
|
|
|
|
|
|
|
|
2sin 11x + 2sin |
5x + -π- |
= 0, или sin 11x + sin 5x + |
-π- |
= 0. |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
3. Используя формулу суммы синусов, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
11x + 5x + -π- |
|
|
|
11x – 5x – -π- |
|
|
|
|
|
|
|
|
|
|
2sin ---- |
--- |
----- |
-----2--------- |
---- |
----6-- cos - |
----------- |
----- |
2-------------- |
--6-- |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
8x + |
π |
|
cos |
|
3x – |
π |
= 0. |
|
|
|
|
|
|
|
|
|
|
---- |
|
|
12------ |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Остается решить последнее уравнение; в результате получаем |
ответ: x = – --π---- |
+ π----k-- |
, x = |
7----π-- + |
π----k-- , k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
|
96 |
|
8 |
|
|
|
|
36 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а м е ч а н и е. Это уравнение можно решить иначе, если сумму |
3 sin 5x + cos 5x преобразовать та : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 sin 5x + cos 5x = 2 |
|
|
3 |
sin 5x + |
1 |
cos 5x |
|
= |
|
|
|
|
---2---- |
-2- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
sin |
π |
sin 5x + cos |
π |
|
cos 5x |
|
= 2cos |
|
5x |
– |
π |
|
. |
|
|
|
|
3-- |
|
|
|
|
|
|
3-- |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
То$да в данном уравнении сла$аемое 2sin 11x следует заменить на
2cos |
π |
– 11x |
|
и записать уравнение в виде |
|
|
|
-- |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2cos |
π |
– 11x |
|
+ 2cos |
|
5x |
π |
= 0, |
|
|
|
|
-- |
|
|
– -- |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
а затем преобразовать сумму осинусов в произведение и т. д.
К упражнению 1з
|
|
|
π |
|
|
1. Найдем ОДЗ уравнения: x − -- + πk, k Ý Z. |
|
|
|
|
|
2 |
|
|
2. Положим y = sin2 x; то$да cos2 x = 1 – y и данное уравнение пре- |
образуется та |
|
|
|
1 |
– 3 = 0; 2y(1 – y) + 1 – 3(1 – y) = 0; 2y |
2 |
– 5y + 2 = 0. |
2y + ------------ |
|
1 – y |
|
|
|
|
|
|
1 |
|
|
Последнее уравнение имеет орни y1 = 2; y2 = -- . |
|
|
|
|
|
2 |
|
|
3. Подставив sin2 x вместо y, получим: |
|
|
а) sin2 x = 2 — это уравнение не имеет решений; |
|
|
б) sin |
2 |
x |
1 |
|
|
|
= -- — это уравнение решим следующим образом: |
|
|
|
2 |
|
|
2sin2 x = 1; 1 – cos 2x = 1; |
cos 2x = 0, |
от уда |
|
|
|
|
|
|
|
|
|
|
|
π |
π k |
, k Ý Z. |
|
|
|
|
x = -- + |
------ |
|
|
|
|
4 |
2 |
|
|
|
|
4. Та а cos |
2 |
x |
− 0 при x = |
π |
π k |
, то среди найденных значе- |
|
-- |
+ ------ |
|
|
|
|
4 |
2 |
|
|
|
ний нет посторонних орней. |
|
|
|
|
|
З а м е ч а н и е. |
Это уравнение можно решить иначе, пола$ая |
cos2 x = y; то$да получим |
|
|
|
|
|
|
|
|
1 |
или |
2y |
2 |
+ y – 1 = 0. |
2(1 – y) + -- – 3 = 0, |
|
|
|
|
y |
|
|
|
|
|
Корнями последне$о уравнения являются y1 = –1; y2 |
1 |
= -- . |
|
|
|
|
|
|
|
2 |
Подставив cos2 x вместо y, получим: |
|
а) cos2 x = –1 — это уравнение не имеет решений; |
|
б) cos |
2 |
x |
1 |
, или 2cos |
2 |
x = 1, от уда 1 + cos 2x = 1, т. е. cos 2x = 0, |
|
= -- |
|
|
|
|
2 |
|
|
|
|
|
|
π |
+ |
π k |
|
|
|
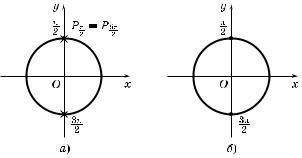
от уда x = -- |
------ , k Ý Z. |
|
|
|
|
|
4 |
|
2 |
|
|
|
К упражнению 2а
З а м е ч а н и е. При решении рассмотренных ниже довольно простых с виду три$онометричес их уравнений учащиеся часто допус ают $рубую ошиб у. Эта ошиб а за лючается в том, что хотя они предварительно находят область допустимых значений, но при записиорней уравнения ее совершенно не учитывают.
1. Требуется решить уравнение 1 + cos2x = 0.
---------------------------
cosx
2. Найдем ОДЗ уравнения:
cos x − 0, т. е. x − π + πk, k Ý Z.
--
2
3. Для на$лядности числа x = π + πk, не входящие в ОДЗ, отметим
--
2
на единичной о ружности « рести ами» (рис. 168, а).
|
|
π |
|
π |
|
3π |
4. Если k = 0, то x = -- |
; если k = 1, то x = -- |
+ π = ------ ; если k = 2, |
|
|
2 |
|
2 |
|
2 |
π |
5π |
|
π |
5π |
отличаются дру$ от |
то x = -- |
+ 2π = ------ |
и т. д. Та а числа -- |
и ------ |
2 |
2 |
|
2 |
2 |
|
|
дру$а на 2π, то соответствующие этим числам точ и единичной о -
ружности совпадают |
|
анало$ично совпадут точ и, соответствующие |
|
|
|
|
|
|
3π |
7π |
. |
|
|
|
числам ------ |
и ------ |
|
|
|
2 |
2 |
|
|
|
|
5. Теперь найдем орни данно$о уравнения. Имеем 1 + cos 2x = 0, |
|
|
|
|
π |
+ πk, k Ý Z. |
от уда cos 2x = –1, т. е. x = -- |
|
|
|
|
2 |
|
6. Отметим эти значения на единичной о ружности сплошными точ ами (рис. 168, б).
Рис. 168


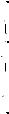


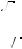



 5 sin y + 10 = a + 2
5 sin y + 10 = a + 2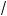 11 и b =
11 и b = 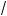 5 ; б) a =
5 ; б) a = 
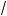 7 +
7 + 
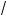 10 и b =
10 и b = 
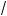 6 +
6 + 
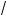 11 .
11 .
 x
x |x + 1|
|x + 1| 
 x
x |x – 2|
|x – 2|  2
2