
К упражнению 1ж |
|
|
|
|
|
|
|
1. Запишем данную фун цию в виде |
|
|
y = ln |
1------+-----2----x-- |
= ln |
1-----+------2----x-- 1/2 |
= |
|
|
|
|
1 – 2x |
|
1 – 2x |
|
= 1-- ln |
1-----+------2----x-- |
= 1-- [ln (1 + 2x) – ln (1 – 2x)]. |
2 |
1 – 2x |
2 |
|
|
|
|
2. То:да получим |
|
|
|
|
|
|
|
y′ = |
1-- |
[ln (1 + 2x) – ln (1 – 2x)]′ = |
|
|
2 |
|
|
|
|
|
|
= |
1 |
|
|
2 |
2 |
= |
2 |
. |
-- |
----------------- + |
---------------- |
1-----–------4----x----2 |
|
2 |
|
1 + 2x |
1 – 2x |
|
З а м е ч а н и е. Если требуется продифференцировать ло:арифмичес ую фун цию, оторая содержит выражение, подлежащее ло:а- рифмированию (произведение, частное, степень, орень), то полезно сначала выполнить ло:арифмирование ( а это было сделано выше).
К упражнению 1з
Дифференцируя произведение и используя формулу для производной по азательной фун ции, а та же сложной фун ции, находим
y′ = (cos 2x · e2cos2x )′ = (cos 2x)′ e2cos2x + cos 2x(e2cos2x )′ =
=–2sin 2x · e2cos2x + cos 2x · e2cos2x · 4cos x (–sin x) =
=–2sin 2x · e2cos2x – 2sin 2x cos 2x · e2cos2x =
=–2sin 2x · e2cos2x (1 + cos 2x) = –4sin 2x cos2 x · e2cos2x .
Купражнению 1и
Находим
|
y′ = (3tg x)′ = 3tg x · ln 3 · (tg x)′ = 3----tg------x---ln-------3- . |
|
|
|
|
|
|
|
cos2 x |
|
К упражнению 1 |
|
|
|
|
|
Имеем |
|
|
|
|
|
|
|
y′ = |
ex – e–x ′ |
= |
(ex – e–x) ′(ex + e–x) – (ex + e–x)′(ex – e–x) |
= |
e----x----+------e---–---x- |
---------------------------------------------(--e---x----+------e---–---x----)--2------ |
--------------------------------------- |
|
|
|
|
|
= |
(ex |
+ e–x)2 – (ex – e–x)2 |
4 |
. |
|
|
---------- |
-------- |
----------------------------------------------- = |
------------------- |
|
|
|
|
|
(ex + e–x)2 |
(ex + e–x)2 |
|

К упражнению 2 |
|
|
|
|
1. |
Найдем производную данной фун ции: |
|
|
|
|
|
9 |
|
|
y′(x) = (12x – 9tg x + 1)′ = 12 – --------------- . |
|
|
|
|
|
cos2 x |
|
2. |
|
9 |
|
|
|
Из уравнения 12 – --------------- = 0 находим |
|
|
cos2 x |
|
|
|
|
|
|
3 |
(1) |
|
|
cos x = ä------- . |
|
|
|
|
2 |
|
3. |
Решив уравнение (1), получим |
|
|
cos x = |
3 |
, x = ä |
π |
(2) |
|
------- |
-- + 2πk, k Ý Z; |
|
|
2 |
|
6 |
|
|
cos x = – |
3 |
, x = ä |
5π |
(3) |
|
------- |
------ + 2πk, k Ý Z. |
|
|
2 |
|
6 |
|
4. |
Серии орней (2) и (3) можно объединить в одну: |
|
|
x = |
π |
|
|
|
ä-- + πk, k Ý Z. |
|
|
|
|
6 |
|
|
К упражнению 3 |
|
|
|
|
1. |
Запишем уравнение |
асательной в общем виде: |
|
|
y – y0 = y′(x0)(x – x0). |
(1) |
2. |
Находим: |
|
|
|
|
а) y0 = y(x0) = 2 · 0 – 5 · 0 + 1 = 1;
б) y′(x) = (2x – 5sin x + 1)′ = 2 – 5cos x, т. е. y′(0) = 2 – 5 = –3. 3. Подставив найденные значения в уравнение (1), получим
|
y – 1 = –3(x – 0), |
или y = –3x + 1. |
К упражнению 4 |
|
|
1. |
Запишем данную фун цию в виде |
|
y = 2x + 1 – (cos2 2x – sin2 2x) – 6 = |
2x + 1 – cos 4x – 6. |
2. |
Находим: |
|
|
а) y0 = y(x0) = –6; |
|
|
|
|
1 |
+ 4sin 4x, от уда y′(0) = 1. |
б) y′(x) = ( 2x + 1 – cos 4x – 6)′ = --------------------- |
|
|
2x + 1 |
|
3. |
Теперь составим уравнение |
асательной: |
|
y – (–6) = 1 · (x – 0), или y + 6 = x, т. е. y = x – 6. |
К упражнению 5
1. Найдем производную данной фун ции:
y′(x) = |
3ctg |
|
4x + |
-π- |
+ x9/5 + 5 ′ = –------------- |
-- |
12--------------- |
----- |
|
|
|
|
2 |
|
|
|
π |
|
|
|
|
|
2 |
|
|
|
|
|
|
sin |
|
4x + |
2-- |
При x0 = 0 получим y′(0) = –12. |
|
|
2. |
Найдем значение фун ции при x0 = 0: |
|
|
y(0) = 3ctg |
π |
|
|
|
-- + 0 + 5 = 5. |
|
|
|
2 |
|
|
3. |
Составим уравнение асательной |
:рафи у в точ |
е (0; 5): |
|
y – 5 = –12(x – 0), |
т. е. |
y = –12x + 5. |
|
К упражнению 6 |
|
|
|
1. |
Находим производную данной фун ции: |
|
|
|
|
6 |
|
|
y′(x) = (3 – 6tg x)′ = –--------------- . |
|
|
|
|
cos2 x |
|
2. |
У:ловой оэффициент прямой y = –6x – 5 равен (–6). |
3. |
Пусть a — абсцисса точ и |
|
6 |
= –6, от уда |
асания; то:да – --------------- |
|
|
|
cos2 a |
|
cos2 a = 1, или cos a = 1, cos a = –1, т. е. a = πk, k Ý Z. |
|
4. |
Найдем значение данной фун ции в точ ах асания: |
|
y0 = y(πk) = 3 – 6tg πk = 3. |
|
5. |
Составим уравнения асательных: |
|
|
y – 3 = –6(x – πk), или y = –6x + 3 + 6πk, k Ý Z.
К упражнению 7 |
|
1. |
Найдем производную данной фун ции: |
|
y′(x) = (3cos x – 4x)′ = –3sin x – 4. |
2. |
У:ловой оэффициент прямой y = –x – 2 есть (–1). |
3. |
Обозначим через a абсциссу точе |
асания; то:да получим урав- |
нение |
|
|
|
|
π |
|
–3sin a – 4 = –1, от уда a = –-- + 2πk, k Ý Z. |
|
|
2 |
4. |
Среди множества найденных точе |
наименее удалена от начала |
|
π |
|
оординат точ а a = –-- (при k = 0). |
|
|
2 |
|
5. Имеем y |
|
= y |
|
|
π |
|
= 3cos |
|
|
π |
– 4 |
|
|
π |
= 2π. |
|
|
|
|
|
–-- |
|
|
–-- |
|
–-- |
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
6. Составим уравнение |
|
асательной в точ е |
|
π |
; 2π |
: |
|
–-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
y – 2π = – |
|
x |
– |
|
π |
, |
или |
|
y = –x + |
3π |
|
|
|
|
–-- |
|
|
------ . |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
К упражнению 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Находим производную данной фун ции: |
|
|
|
|
|
|
y′(x) = |
|
–2sin |
|
x + |
π ′ |
= –2cos |
|
x |
+ |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
2. По условию у:ловой |
|
оэффициент |
|
асательной в ис омой точ е |
равен значению фун |
|
ции в этой же точ е: |
|
|
|
|
|
|
|
|
|
|
|
–2sin |
|
|
x |
|
|
π |
= –2cos |
|
x |
+ |
π |
. |
|
|
(1) |
|
|
|
|
|
+ -- |
|
|
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
3. Решим уравнение (1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x + |
π |
|
= cos |
x + |
π |
; tg x + |
π |
|
= 1, |
|
-- |
-- |
-- |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
+ πk, k Ý Z. |
|
от уда x + -- = |
-- + πk, k Ý Z. Ита |
, x = –------ |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
К упражнению 13а
1.Находим значение фун ции при x0 = 5: f(5) = 1.
2.Далее имеем
f′(x) = (e5 – x(3x – 14)4)′ = (e5 – x)′(3x – 14)4 + ((3x – 14)4)′e5 – x =
=–e5 – x(3x – 14)4 + 12(3x – 14)3e5 – x =
=e5 – x(3x – 14)3(12 – 3x + 14) = e5 – x(3x – 14)3(26 – 3x),
от уда f′(5) = 11.
3. Составим уравнение асательной:
y – 1 = 11(x – 5), или y = 11x – 54.
К упражнению 14а
1. Найдем производную данной фун ции:
f′(x) = (11x · ln 29 – 29x · ln 11)′ =
= 11x · ln 11 · ln 29 – 29x · ln 11 · ln 29 = ln 11 · ln 29 · (11x – 29x).
2. По условию асательная перпенди |
улярна оси ординат, т. е. па- |
раллельна оси абсцисс. Та им образом, получаем уравнение |
ln 11 · ln 29 · (11x – 29x) = 0, |
от уда x = 0. |
К упражнению 15а
1. Имеем
f′(x) = (14x – 1)′ = 14x · ln 14.
2. |
У:ловой |
оэффициент прямой y = xln 14 – 20 равен ln 14. |
3. |
Та |
а |
|
|
асательная параллельна заданной прямой, то их у:ло- |
вые оэффициенты равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14x · ln 14 = ln 14, |
или |
14x = 1, т. е. x = 0. |
4. |
При x = 0 находим f(0) = 0. |
|
|
|
|
|
|
|
|
|
|
|
К упражнению 16а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Сначала найдем производную данной фун ции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5( 4x – 1) |
|
f′(x) = ((4x – 1)ln (5x + 3))′ = 4 ln (5x + 3) + ------------------------- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x + 3 |
2. |
Теперь найдем у:ловой |
оэффициент |
асательной в точ е с абс- |
циссой x0 |
|
2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= –-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–-- |
|
– 1 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
5 |
|
|
|
f′ |
|
= 4 ln |
5 |
|
+ 3 |
+ ------------------------------------ = –13. |
|
|
|
–-- |
|
|
|
–-- |
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
2 |
+ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
К упражнению 17а
1. Напомним формулу перехода от одно:о основания ло:арифма дру:ому:
log N = logbN .
---------------
a logba
2. Используя эту формулу, преобразуем выражение ln 2 · log2 (3x +
+ 1). Имеем:
а) log (3x + 1) = ln (3x + 1) ;
2 -----------------------------
ln2
б) ln 2 · log2 (3x + 1) = ln 2 ·
-----------------------------
ln (3x + 1) = ln (3x + 1).
ln2

3. |
То:да заданная фун ция примет вид |
|
|
f(x) = 4x – 3 – ln (3x + 1). |
(1) |
4. |
Найдем производную фун ции (1): |
|
|
f′(x) = (4x – 3 – ln (3x + 1))′ = 4 – |
3 |
|
----------------- . |
|
|
3x + 1 |
5. По условию у:ол, оторый образует асательная с положительным направлением оси абсцисс, есть α = arctg 3. Это означает, что tg α = 3, т. е. у:ловой оэффициент асательной равен 3.
6. |
Для отыс ания абсциссы точ и |
асания составим уравнение |
|
3 |
= 3, |
|
4 – ----------------- |
|
3x + 1 |
|
|
2 |
|
от уда находим x = -- . |
|
|
3 |
|
К упражнению 18 |
|
1. |
Найдем производную данной фун ции: |
y′ = (sin x – 
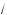 3 cos x)′ = cos x +
3 cos x)′ = cos x + 
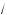 3 sin x.
3 sin x.
2. |
Та а |
асательная параллельна оси Ox, то ее у:ловой |
оэф- |
фициент равен нулю, т. е. y′ = 0. |
|
|
|
3. |
Следовательно, получаем уравнение |
|
|
|
|
|
1 |
, |
|
|
|
cos x + 3 sin x = 0, или tg x = –------- |
|
|
|
|
3 |
|
|
от уда |
|
|
|
|
|
|
π |
+ πk, k Ý Z. |
|
(1) |
|
|
x = –-- |
|
|
|
6 |
|
|
|
4. |
Из серии |
орней (1) отрез |
у [3; 6] принадлежит толь о один о- |
π |
11 |
π |
(при k = 2). Ита |
11 |
π |
11 |
· 3,14 d 5,8. |
рень x = – -- |
+ 2π = ---------- |
, x = ---------- |
d ------ |
6 |
6 |
|
|
6 |
|
6 |
|
К упражнению 20а
1. Найдем производную и приравняем ее нулю:
f′(x) = |
|
1 |
|
|
′ |
= cos x – sin 2x; |
|
|
sin x + -- |
cos 2x- |
|
|
|
2 |
|
|
|
|
|
cos x – sin 2x = 0; |
cos x(1 – 2sin x) = 0. |
(1) |

2. Решив уравнение (1), получим
cos x = 0, |
π |
+ πk, k Ý Z; |
(2) |
x = -- |
|
|
2 |
|
|
1 |
, |
π |
+ 2πk, k Ý Z; |
(3) |
sin x = -- |
x = -- |
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5π |
+ 2πk, k Ý Z. |
|
(4) |
|
|
|
|
|
|
|
|
|
x = ------ |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
3. Из серий |
орней (2)—(4) заданному отрез у [0; π] принадлежат |
|
π |
, x2 |
π |
, x3 |
= |
5π |
|
|
|
|
|
|
|
три орня: x1 = -- |
= -- |
------ . |
|
|
|
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
4 Вычислим значения фун ции в найденных точ ах и на онцах |
данно:о отрез |
а: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
f |
π |
= |
3 |
, |
f |
π |
|
1 |
, f |
5π |
|
3 |
, |
1 |
f(0) = -- |
-- |
-- |
-- |
= -- |
------ |
= -- |
f(π) = -- . |
2 |
|
|
6 |
|
4 |
|
|
2 |
|
2 |
|
6 |
|
4 |
|
2 |
5. Ита , fнаиб |
– fнаим |
= |
3 |
– |
1 |
|
1 |
|
|
|
|
|
|
-- |
-- |
= -- . |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
4 |
|
|
|
|
|
|
К упражнению 21а
1.Область определения D(f) : x > 0, т. е. x Ý (0; +×).
2.Фун ция не является ни четной, ни нечетной.
3.Фун ция непериодичес ая.
4. |
Промежут и зна опостоянства: а) y > 0 при x > 1; б) y < 0 при |
0 < x < 1 (рис. 203). |
|
|
5. |
Находим производную |
|
|
|
f′(x) = ( x ln x)′ = -----1------ ln x + |
x · 1-- |
= x-----ln------x-----+------2----x-- , |
|
2 x |
x |
2x x |
|
|
а затем — ритичес ие точ и фун ции:
|
x( lnx + 2) |
= 0, x(ln x |
+ 2) = 0, x |
|
− 0, ln x = –2, x |
|
|
|
|
|
|
1 |
|
|
----------------------------- |
1 |
2 |
= e–2 = ----- . |
|
2x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
6. С помощью рис. 204 устанавливаем, что при 0 < x < |
1 |
фун - |
----- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
фун ция имеет ми- |
ция убывает, а при x > ----- |
возрастает. При x = ----- |
|
|
|
|
|
|
e2 |
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
нимум: f |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= f ----- |
= –-- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
e2 |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К упражнениям 21в,
См. соответственно рис. 209 и 210.
К упражнению 22а
1.Решив неравенство |x – 3| m 1, или –1 m x –3 m 1, получим x Ý [2; 4].
2.Рассмотрим фун цию
|
|
y(x) = 4x2 – 9kx + 2k2. |
(1) |
|
3. Для то:о чтобы фун ция (1) была |
|
|
отрицательной на отрез е [2; 4], нужно, |
|
|
чтобы выполнялась система неравенств |
|
|
(рис. 211) |
|
|
|
|
|
|
|
f(2) < 0, |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(4) < 0. |
|
|
|
|
|
|
|
|
|
|
|
4. Решим систему (2): |
|
|
|
|
|
|
16 – 18k + 2k2 < 0, |
|
1 < k < 8, |
|
|
|
64 – 36k + 2k2 < 0, или |
|
2 < k < 16, |
|
|
|
|
|
|
Рис. 211
от уда 2 < k < 8.
К упражнению 24а
1. Преобразуем первое неравенство системы:
x2 + 6x + 9 – 9 + y2 – 2y + 1 – 1 + 9 m 0,
или
(x + 3)2 + (y – 1)2 m 1. |
(1) |
2. Неравенство (1) задает на плос ости множество точе , лежащих внутри и на :ранице ру:а, имеюще:о радиус 1 и центр в точ е (–3; 1) (рис. 212, а).
3.Рассмотрим второе неравенство системы для следующих четырех случаев:
а) если x l –1, y l 1, то неравенство примет вид y m x; б) если x m –1, y l 1, то оно примет вид y m –x – 2;
в) если x l –1, y m 1, то оно примет вид y l –x + 2; :) если x m –1, y m 1, то оно примет вид y l x + 4.
4.Пересечение множеств решений полученных неравенств определяет множество решений второ:о неравенства системы. Это множество на рис. 212, б заштриховано.
5.На онец, пересечение множеств решений перво:о неравенства системы (рис. 212, а) и ее второ:о неравенства (рис. 212, б) определяет множество решений исходной системы. Этим множеством является фи:ура, заштрихованная на рис. 212, в.
6.Найдем площадь полученной фи:уры:
1 |
π · 1 |
2 |
π |
( в. ед.). |
S = -- |
|
= -- |
4 |
|
|
4 |
|
К упражнению 25а |
|
1. |
Данное уравнение равносильно системе условий |
|
|
|
x2 – 7x + 12 = 0, |
(1) |
|
|
|
|
|
|
32x – a – 3a – x − 0. |
(2) |
|
|
2. |
Находим орни уравнения (1): x1 = 3, x2 = 4. |
|
460






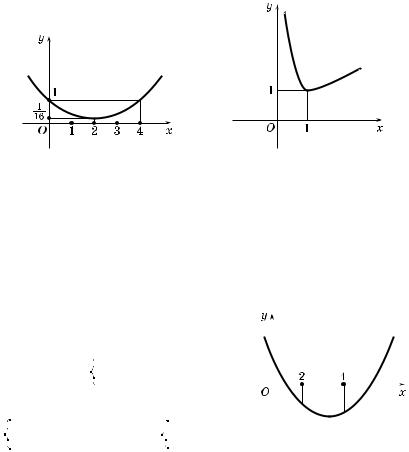



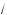 3 cos x)′ = cos x +
3 cos x)′ = cos x + 
 3 sin x.
3 sin x.