Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
К упражнению 9б
1. Пусть 3x = y. То,да данное уравнение примет вид
y2 – 2(2a + 1)y – 5a2 + 34a – 24 = 0. (1) 2. Найдем дис риминант уравнения (1):
D---- = (2a + 1)2 + 5a2 – 34a + 24 = (3a – 5)2.
4
3. Найдем орни уравнения (1):
y1 = 2a + 1 – (3a – 5) = 6 – a, y2 = 2a + 1 + 3a – 5 = 5a – 4.
4. Для то,о чтобы исходное уравнение имело два различных орня, необходимо выполнение следующих условий:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
y1 − y2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
a − -- , |
|
|||
|
|
|
|
|
6 – a − 5a – 4, |
|
|
|
|
3 |
|
||||||||
|
y1 > 0, |
|
|
или |
|
6 – a > 0, |
|
|
т. е. |
|
a < 6, |
|
|||||||
|
y2 > 0, |
|
|
|
|
|
5a – 4 > 0, |
|
|
|
|
|
-- |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
Ответ: a Ý |
4 |
5 |
|
5 |
|
|
. |
|
|
|
|
|
|
a > |
5 . |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
-- ; |
-- |
|
-- ; 6 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
К упражнению 10а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
π x |
> 0, |
sin |
π x |
− 1. |
|
|
|
|
|
|
|
|
|||||
1. Здесь sin ------ |
------ |
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2. Из данно,о уравнения следует, что |
|
|
|
|
|
|
|
||||||||||||
2π x |
+ sin |
π x |
|
|
|
|
|
|
π x |
|
π x |
+ sin |
π x |
= 0, |
|||||
sin ---------- |
------ + 1 = 1, или 2sin ------ cos |
------ |
------ |
||||||||||||||||
3 |
|
|
3 |
|
|
|
|
|
|
3 |
|
3 |
|
|
3 |
|
|||
от уда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π x |
2cos |
π x |
|
|
= 0. |
|
|
|
|
(1) |
|||
|
|
|
|
|
sin ------ |
|
------ + 1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
π x |
не обращается в нуль, поэтому |
|||||||
3. В уравнении (1) множитель sin ------ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π x |
= – |
1 |
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
cos ------ |
-- . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
π x
4. Учитывая, что sin ------ > 0, запишем решение уравнения (2):
3
π x 2π
------ = ------ + 2πn, n Ý Z, или x = 2 + 6n, n Ý Z.
3 3
501
К упражнению 11а
1. Для нахождения ОДЗ данно,о неравенства нужно решить неравенство x2 – 8|x| + 7 l 0. Оно равносильно сово упности двух систем:
а) |
|
x l 0, |
или |
|
x l 0, |
||||
|
|
||||||||
|
|
||||||||
|
x2 – 8x + 7 l 0, |
|
(x – 1)(x – 7) l 0, |
||||||
|
|
||||||||
от уда x Ý [0; 1] [7; +×); |
|
|
|
|
|
||||
б) |
|
|
|
x < 0, |
или |
|
|
|
x < 0, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
x2 + 8x + 7 l 0, |
|
|
|
(x + 7)(x + 1) l 0, |
||
|
|
|
|
||||||
от уда x Ý (–×; –7] [–1; 0).
2.Объединив решения систем а) и б), получим x Ý (–×; –7] [–1; 1] [7; +×).
3.При решении исходно,о неравенства
x2 – 8 |
x |
+ 7 > x + 2 |
(1) |
следует рассмотреть два случая: x + 2 < 0 и x + 2 l 0.
а) Если x + 2 < 0, т. е. x < –2, то правая часть неравенства (1) отрицательна и, значит, множеством решений это,о неравенства является промежуто (–×; –7].
б) Если же x + 2 l 0, т. е. x l –2, то правая часть неравенства (1) положительна, а потому обе части это,о неравенства можно возвести
в вадрат: |
|
x2 – 8|x| + 7 > x2 + 4x + 4. |
(2) |
4. Дальнейшие рассуждения связаны с двумя возможными промежут ами изменения x: x l 0 и x < 0.
а) Если x l 0, то неравенство (2) примет вид –8x + 7 > 4x + 4, от у-
1 |
, т. е. множеством решений является промежуто |
|
|
1 |
. |
||||||||||||
да x < -- |
|
|
0; -- |
||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
б) Если же x < 0, то неравенство (2) примет вид 8x + 7 > 4x + 4, от- |
|||||||||||||||||
уда x > – |
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
; 0 . |
|
||
-- , т. е. множество решений есть промежуто |
–-- |
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
5. Объединив найденные решения неравенства (2), получим про- |
|||||||||||||||||
межуто |
|
3 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
–-- ; -- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Ита |
, решением исходно,о неравенства (1) является множество |
||||||||||||||||
значений x та |
их, что x Ý |
|
–×; –7 |
|
|
|
3 |
1 |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||
|
|
|
–-- |
; -- |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
||
502
П Р И Л О Ж Е Н И Е
Варианты билетов для вст пительных письменных э заменов
Варианты I—X и XI—XX в разные ,оды предла,ались на э заменах в РЭА им. Г. В. Плеханова, а варианты XXI—XXX — в МИУ им. С. Орджони идзе ( вариантам XI—XXX приведены ответы).
Ва р и а н т I
1.Упростите до числово,о значения выражение
1-----–------a---–1-------⁄--2- |
– a----1---/--2----–-----a----–1------/--2- |
· |
------- |
------------------a--- |
----------- |
--- |
---- . |
|
1 + a1 / 2 |
|
a – 1 |
|
(1 – a)(1 – a)–1 |
||||
2. Вычислите |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 – |
1 |
|
2 |
92 + log3 2 |
+ 3 · 45 – log 2 4 |
|
-- log |
|||||
|
: 16 |
2 |
4 |
. |
||||
|
|
|
|
|
|
|
|
|
3. Упростите до числово,о значения выражение
tg |
π |
+ α |
|
· |
cos 2α |
. |
-- |
|
1------+-----sin----------2----α-- |
||||
|
4 |
|
|
|
4. Найдите решения уравнения
3 log2 (2 – x) – log22 (2 – x) = 3 – log2 – x (2 – x)3.
В ответе запишите оличество решений.
5. Найдите решения уравнения 
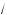3 cos x + 4 cos2 x sin x = 0, принадлежащие отрез у [0; π]. В ответе запишите оличество решений.
6. Найдите множество решений неравенства
|
1 |
|
13---------x----+------9-- – x |
|
1 |
|
|
x |
+ 5 |
l |
. |
||||
-- |
|
27------ |
|||||
|
3 |
|
|
|
|
|
|
В ответе запишите наименьшее целое решение. 7. Найдите точ у ма симума фун ции
y = |
|
1 |
2 |
|
7 |
. |
|
x – -- |
|
|
x + -- |
||
|
2 |
4 |
|
В ответе запишите значение фун ции в точ е ма симума.
503
8. Э с аватор вырыл траншею длиной 15 м, а затем в е,о работе произошел перерыв. После перерыва э с аватор вырыл вторую траншею длиной 12 м. Перерыв и рытье второй траншеи заняло на 24 мин больше, чем рытье первой траншеи. Если бы производительность э с- аватора была в 3 раза больше, то на рытье первой траншеи он затратил бы время, равное времени перерыва. Определите производительность э с аватора, т. е. длину траншеи (в метрах), оторую он рыл в
течение 1 ч.
9. В треу,ольни , у оторо,о длина основания равна 30 см, а длина высоты равна 10 см, вписан равнобедренный прямоу,ольный тре- у,ольни та , что е,о ,ипотенуза параллельна основанию данно,о тре- у,ольни а, а вершина прямо,о у,ла лежит на этом основании. Найдите длину ,ипотенузы.
10. Точ а O является центром симметрии уба ABCDA1B1C1D1.
Разложите ве тор OC по ве торам AB1 , AD1 и AA1 . В ответе запишите сумму оэффициентов разложения.
Ва р и а н т II
1.Упростите до числово,о значения выражение
-------1-----–-----a----–2---------- |
– 2a–3/2 |
+ ------- |
a----–2-------–-----a--------- |
· 3----(---a----2----+-----2----)---–1---- . |
|
a1 / 2 – a–1/ 2 |
|
|
a1 |
/ 2 – a–1 ⁄ 2 |
2a–3 / 2 |
2. Вычислите |
|
|
|
|
|
|
|
|
|
|
1 |
21 – log 24 |
|
2 + log216 : 10 |
3 – -- lg4 |
||
· 4 |
2 . |
||||
|
|
|
|
|
|
3. Упростите до числово,о значения выражение
tg |
π |
α |
+ tg |
π |
α |
|
|
2cos |
2 α |
– 1 |
|
. |
||
|
||||||||||||||
-- |
– --- |
|
-- |
+ --- |
|
|
|
--- |
|
|||||
|
4 |
2 |
|
4 |
2 |
|
|
2 |
|
|
||||
4. Найдите решения уравнения
log3 |x – 1| = 1 + log3 (x + 2).
В ответе запишите оличество решений.
5. Найдите решения уравнения 
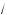2 cos x – sin 2x = 0, принадлежащие отрез у [–π; π]. В ответе запишите оличество решений.
6. Найдите множество решений неравенства
|
2 |
|
4 |
|
3 + x |
|
x + 2 |
|
|
||
|
------------- |
m |
|
|
|
(0,8) |
|
-- |
. |
||
|
|
|
5 |
|
|
В ответе запишите наибольшее решение неравенства.
504
7. Найдите точ у ма симума фун ции
x2 – 2x + 1
y = ------------------------------ . x + 1
В ответе запишите значение фун ции в точ е ма симума.
8. Рабочий из,отовил 180 деталей и сделал перерыв. После перерыва нему присоединился второй рабочий и они вместе из,отовили еще 420 деталей. За время перерыва рабочие вдвоем смо,ли бы из,отовить 60 деталей. Перерыв и совместная работа заняли на 1 ч больше, чем время, затраченное на из,отовление 180 деталей. Определите
оличество деталей, из,отовленных одним рабочим за час, если оно
уаждо,о из рабочих одина ово.
9.В равнобедренном треу,ольни е ABC длина основания AC равна 15 см, а длина высоты AE равна 12 см. Найдите площадь треу,ольни а.
10.В правильной треу,ольной пирамиде ABCD точ а M — середина стороны основания BC; точ а K лежит на ребре DB, причем KB =
= 2DK. Разложите ве тор MK по ве торам AC , AB и AD . В ответе запишите наименьший из оэффициентов разложения.
Ва р и а н т III
1.Упростите до числово,о значения выражение
|
(1 – 2a–1/2 + a–1) ---- |
-1-----–-----a----–2------ |
--- |
–1 |
– |
1-----+------a----–1------/--2- |
- –1 . |
|
|||||||||||||
|
|
|
|
|
|
|
|
a + a–1/ 2 |
|
a1/2 – 1 |
|
|
|
|
|
||||||
2. Вычислите |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
-- log5 |
27 |
|
log |
25 |
4 |
|
1 |
|
|
log |
10 |
log |
8 |
8 |
|
|||||
|
25 |
3 |
|
– 5 |
|
|
+ |
· 10 |
|
: 64 |
|
|
|
. |
|||||||
|
|
|
|
|
|
-2- |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Упростите до числово,о значения выражение |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 cos2 α – 1 |
|
. |
|
|
|
|
|
||||||
|
|
|
|
-- |
------- |
--- |
---π----- |
------ |
------ |
----- |
----- |
2------π---------- |
----- |
|
|
|
|
|
|||
|
|
|
|
8 tg |
|
|
cos |
|
|
|
|
|
|
||||||||
|
|
|
|
|
-- |
– α |
|
|
-- – |
α |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
||
4. Найдите решения уравнения |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
(x |
2 |
– x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- log |
|
= 12. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
x2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
В ответе запишите |
оличество решений. |
|
|
|
|
|
|
|
|||||||||||||
5. Найдите решения уравнения cos x – cos 2x = sin2 x, принадле- |
|||||||||||||||||||||
жащие отрез у [–π; 2π]. В ответе запишите |
оличество решений. |
||||||||||||||||||||
505
6. Найдите множество решений неравенства
|
|
|
5 |
|
|
|
|
|
|
3 |
|
1 |
|
------------- |
|
|
1 |
|
------------- |
||
2 – |
x |
< |
x |
+ 2 . |
||||||
-- |
|
-- |
|
|||||||
|
3 |
|
|
|
|
|
3 |
|
|
|
В ответе запишите наибольшее целое решение.
7. Найдите ма симум фун ции y = (x – 5)2(2x + 8). В ответе запишите значение фун ции в точ е ма симума.
8. Бри,ада пробурила с важину ,лубиной 1440 м и переехала в дру,ое место, ,де пробурила еще одну с важину ,лубиной 600 м. Бурение первой с важины продолжалось на 1 месяц больше, чем переезд и бурение второй с важины. Если бы первую с важину бри,ада бурила с удвоенной с оростью, то затратила бы время, равное времени переезда. Определите с орость бурения (в метрах за месяц).
9. Длина стороны вадрата ABCD равна 6 см. Точ а M делит сторону CD в отношении 2 : 1, считая от вершины C; пусть E — точ а пересечения прямых AM и BD. Найдите площадь треу,ольни а DEM.
10. Дан уб ABCDA1B1C1D1. Точ а O является центром симметрии ,рани DCC1D1. Разложите ве тор OB по ве торам AB1 , AD1 и
AA1 . В ответе запишите сумму оэффициентов разложения.
Ва р и а н т IV
1.Упростите до числово,о значения выражение
|
|
a |
1/ 2 |
– |
a – a–2 |
– |
1 – a–2 |
– |
2 |
a + 1 –1 |
||||||
|
|
|
a----1---/--2----–-------a--–1------/--2- |
------------- |
+------a----–1------/--2 |
------ |
|
------------- - . |
||||||||
|
|
|
|
|
a1/ 2 |
|
a3 / 2 |
a3 / 2 |
||||||||
2. |
Вычислите |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 + |
1 |
lg 625 |
|
|
|
|
|
|
|
|
|
3 – log1/2 4 |
+ |
2-- |
. |
|
|
||||||
|
|
|
|
|
4 |
|
|
|
100 |
|
|
|
|
|
||
3. |
Упростите до числово,о значения выражение |
|||||||||||||||
|
|
|
sin α + sin α + |
2----π-- |
+ sin α + |
4----π-- |
+ 3. |
|||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
||
4. |
Найдите решения уравнения |
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 log |
8 |
x – 3log2 x = 3 + log |
|
64------ . |
||||||||
|
|
|
|
|
|
|
|
8 |
|
|
x/4 |
x |
3 |
|
||
В ответе запишите |
оличество решений. |
|
|
|
|
|
|
|||||||||
5. |
Найдите решения уравнения 1 + cos 2x = |
|
3 sin 2x, принадле- |
|||||||||||||
жащие отрез |
у [–π; 2π]. В ответе запишите |
оличество решений. |
||||||||||||||
506
6. Найдите множество решений неравенства
|
2 |
|
|
|
|
3 |
|
----------------- |
|
|
|
|
------------- |
|
|
|
3 |
|
x + 5 |
|
(0, 6) |
1 – 2x |
|
||||
|
l |
-- |
. |
|||
|
|
|
|
5 |
|
|
В ответе запишите наибольшее отрицательное решение. 7. Найдите точ у ма симума фун ции
x2 + 4x – 1
y = ------------------------------ . x – 1
В ответе запишите значение фун ции в этой точ е.
8. Пассажир выходит из трамвая на останов е A и идет до почты пеш ом, затратив для это,о на 1 мин больше, чем если бы он проехал дальше на трамвае до останов и B и прошел от B до почты пеш ом. Расстояние от A до почты равно 300 м, а от B до почты — 100 м. Если бы пассажир шел от A до почты с удвоенной с оростью, то он затратил бы на это расстояние та ое же время, что и трамвай на расстояние от A до B Определите с орость пассажира.
9. Площадь треу,ольни а AMC равна 10 см2. Точ а K лежит на продолжении стороны AM, причем MK = 2AM. Найдите площадь тре- у,ольни а AKC.
10. В правильной четыреху,ольной пирамиде ABCDE точ а K — середина бо ово,о ребра EC; точ а M лежит на стороне основания DC,
причем MC = 3DM. Разложите ве тор MK по ве торам AD , AC и AE .
Вответе запишите сумму оэффициентов разложения.
Ва р и а н т V
1. Упростите до числово,о значения выражение
|
|
x4/ 3 – 8x1 / 3y |
|
1 – 2 |
y |
|
1/3 |
|
–1 |
1 |
. |
|
||||
|
|
--------------------------- |
---- |
----------------------- |
-- |
|
|
– ---- |
--------- |
|
||||||
|
|
x2/ 3 + 2(xy)1 / 3 + 4y2/ 3 |
|
|
x |
|
|
|
x |
–2 / 3 |
|
|
||||
2. Вычислите |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
– log |
---------- – 1 |
|
|||
|
|
log 7 3 |
|
3 – -- log |
4 |
|
-- log |
|
4 |
|
|
|
||||
|
|
|
|
|
|
3 27 |
|
|||||||||
|
|
2 |
2 |
|
2 |
|
6 |
|
|
|
|
|||||
|
7 |
+ |
2 |
|
– 3 · 6 |
|
|
|
|
|
: 3 |
|
|
. |
||
3. Упростите до числово,о значения выражение
2 |
α + cos |
π |
– α |
|
cos |
π |
+ α |
|
. |
sin |
-- |
|
-- |
|
|||||
|
|
3 |
|
|
3 |
|
|
4. Найдите решения уравнения
log1/2 |x – 2| = –1 + log1/2 x.
В ответе запишите оличество решений.
507
5. Найдите решения уравнения 
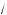3 sin2 x + 0,5 sin 2x = 0, принадлежащие отрез у [–π; π]. В ответе запишите оличество решений.
6. Найдите множество решений неравенства
7x2 + 3x – 7
1 ----------------------------------
2x – 1
-2-
<1 x .-8-
Вответе запишите наименьшее целое решение.
7.Найдите точ у минимума фун ции y = (x + 2)2(2x + 1). В ответе запишите значение фун ции в этой точ е.
8.Бри,ада лесорубов за,отовила 216 м3 древесины и переехала на дру,ое место, ,де за,отовила еще 288 м3 древесины. Переезд занял
время, за оторое бри,ада смо,ла бы за,отовить еще 144 м3 древесины, если бы ее производительность увеличилась вдвое. На за,отов у 216 м3 древесины ушло на 6 дней меньше, чем на переезд и на за,отов- у 288 м3 древесины. Найдите производительность бри,ады, т. е. о-
личество древесины (в м3), за,отавливаемой за день.
9.В равнобедренном треу,ольни е основание равно 30 см, а высота, опущенная на это основание, равна 20 см. Определите длину высоты, опущенной на бо овую сторону треу,ольни а.
10.Дан уб ABCDA1B1C1D1. Точ а O является центром симмет-
рии ,рани D1C1CD. Разложите ве тор OA1 по ве торам AB1 , AD1 и
AA1 . В ответе запишите сумму оэффициентов разложения.
Ва р и а н т VI
1.Упростите до числово,о значения выражение
|
|
----9----a----–------25-------a----–1------- |
– a-----+-------7----+------10-------a----–1---- 2 |
· 3a–1. |
|
|
||||
|
|
3a1 / 2 – 5a1/ 2 |
|
a1 / 2 + 2a–1/ 2 |
|
|
|
|
|
|
2. Вычислите |
|
|
|
|
|
|
|
|
||
|
|
2 – log 3 4 27 |
log5 |
49 |
1 – log 6 |
3 |
|
|
lg 25 |
|
|
9 |
– ( 5) |
|
|
+ 6 |
|
: |
10 |
|
. |
3. Упростите до числово,о значения выражение
sin |
2 π |
+ α |
|
– sin |
2 π |
|
-- |
|
-- |
– α |
|||
|
8 |
|
|
8 |
|
|
- - - - - - - - - |
------------ |
------2-----sin---------2----α--------------- |
--------- . |
|||
|
|
|
||||
4. Найдите решения уравнения
(x2)(logx
8) – 1 = 32.
Вответе запишите оличество решений.
508
5. Найдите решения уравнения
4cos2 x + 0,5sin 2x + 3sin2 x = 3,
принадлежащие отрез у |
|
0; |
3π |
|
. В ответе запишите оличество ре- |
|
|
||||
|
------ |
|
|||
|
|
|
2 |
|
|
шений.
6. Найдите множество решений неравенства
3 x – --
(0, 5) x
2
>------ .
2
Вответе запишите наибольшее целое решение.
7.Найдите точ у минимума фун ции y = (x + 5)2(x – 1). В ответе запишите значение фун ции в этой точ е.
8. Первый насос вы ачал из отлована 12 000 л воды и остановился. После перерыва второй насос вы ачал еще 30 000 л воды. Производительность второ,о насоса вдвое больше, чем у перво,о. За время перерыва первый насос смо, бы вы ачать 3000 л воды. Время перерыва вместе со временем работы второ,о насоса на 1 ч больше, чем время работы перво,о насоса. Найдите производительность перво,о насоса, т. е. оличество литров воды, оторое он вы ачивал за
1мин.
9.В треу,ольни е ABC биссе триса у,ла ACB пересе ает сторону AB в точ е D. Из точ и D проведена прямая, параллельная основанию AC, и пересе ающая сторону BC в точ е E. Длина стороны BC равна 12 см, а длина стороны AC равна 18 см. Определите длину отрез-
аDE.
10.В правильной четыреху,ольной пирамиде ABCDE с вершиной E точ а O — центр основания; точ а K лежит на ребре CE, причем
EK = 3KC. Разложите ве тор OK по ве торам AD , AB и AE . В ответе запишите сумму оэффициентов разложения.
Ва р и а н т VII
1.Упростите до числово,о значения выражение
|
-- |
-----4----a-----–-----9----a----–1---------- |
+ a-----–------4-----+----------3a---–1---- |
· ---1--- . |
|||
|
2a1 / 2 – 3a–1/ 2 |
a 1 / 2 – a –1 / 2 |
a |
|
|||
2. Вычислите |
|
|
|
|
|
|
|
|
49 |
1 – log7 2 |
–log |
6 2 |
–log1 ⁄ 16 |
25 |
|
|
+ 6 |
|
: |
16 |
|
. |
|
|
|
|
|
|
|
|
|
509
3. Упростите до числово,о значения выражение
cosα |
– tg |
π |
– |
α |
. |
1-----+-------sin---------α-- |
|
4 |
|
-2-- |
|
4. Найдите решения уравнения
log2 |x – 3| = 2 + log2 (x + 1).
В ответе запишите оличество решений. 5. Найдите решения уравнения
1 – cos 2x + 4 sin2 x cos x = 0,
принадлежащие отрез у |
|
0; |
3π |
|
. В ответе запишите оличество ре- |
|
|
||||
|
------ |
|
|||
|
|
|
2 |
|
|
шений. |
|
|
|
|
|
6. Найдите множество решений неравенства |
|||||
|
|
3x2 – 6 |
|
||
-- |
|
-------------------- |
l 2–x. |
||
2x |
– 1 |
||||
1 |
|
|
|||
2 |
|
|
|
|
|
В ответе запишите наименьшее целое число, не являющееся решением.
7. Найдите точ у ма симума фун ции
x2 – 3x
y = -------------------- . x + 1
Вответе запишите значение фун ции в этой точ е.
8.На стан е было обработано 400 деталей. После перерыва производительность стан а увеличилась в 2 раза и было обработано еще
1200 деталей за |
время, равное времени |
перерыва. |
Обработ |
а |
||||||||||
400 деталей заняла |
на 0,5 ч меньше, чем |
перерыв и |
обработ |
а |
||||||||||
1200 деталей. Найдите производительность стан а ( |
оличество дета- |
|||||||||||||
лей, обрабатываемых за 1 ч) до перерыва в работе. |
|
|
|
|
|
|||||||||
9. В равнобедренной трапеции ABCD длина основания AD равна |
||||||||||||||
9 см, длина основания BC равна 3 см, длина бо овой стороны равна |
||||||||||||||
5 см. Через вершину B проведена прямая, делящая пополам диа,о- |
||||||||||||||
наль AC и пересе ающая AD в точ |
е K. Найдите площадь треу,ольни- |
|||||||||||||
а BDK. |
|
|
|
|
|
|
|
|
|
|
||||
10. В убе ABCDA1B1C1D1 точ |
а M — середина ребра B1C1, точ- |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
а K лежит на ребре DC, причем KC = 2DK. Разложите ве тор MK по |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||
ве торам AD , AA1 |
и AB1 . В ответе запишите сумму |
оэффициентов |
||||||||||||
разложения. |
|
|
|
|
|
|
|
|
|
|
||||
510