Готовимся к экзамену по математике_Крамор В.С_2008 -544с

Т е м а 17

À

Решение тригонометрических уравнений методом разложения на множители.

Решение тригонометрических уравнений методом введения новой переменной.

Решение тригонометрических уравнений, однородных относительно синуса и косинуса. Решение тригонометрических уравнений вида a cos x + b sin x = c.

Решение простейших тригонометрических неравенств

Теоретичес ие сведения

1. Решение тригонометрических уравнений методом разложения на множители

Применение метода разложения на множители основано на том, что уравнение

f1(x)f2(x) = 0 (*) равносильно сово упности уравнений f1(x) = 0; f2(x) = 0 в области определения уравнения (*).

Пример. Решить уравнение:

а) sin 3x = sin x; б) cos2 x + cos2 2x + cos2 3x = 1,5. Р е ш е н и е. а) Имеем

sin 3x – sin x = 0 _ 2 sin x cos 2x = 0.

Значит, либо sin x = 0, от уда x = πn, n Ý Z, либо cos 2x = 0,

_ 2 cos 4x cos 2x + cos 4x = 0 _ cos 4x (2 cos 2x + 1) = 0.

351

Последнее уравнение равносильно сово упности уравнений cos 4x = 0; 2 cos 2x + 1 = 0. Из перво о уравнения находим 4x =

= π + πn, т. е. x = π + πn , n Ý Z; из второ о получаем cos 2x =

-- -- ------

2 8 4

= – 1 , от уда 2x = ä2π + 2πn, т. е. x = äπ + πn, n Ý Z.

-- ------ --

2 3 3

2. Решение тригонометрических уравнений методом введения новой переменной

Если уравнение, содержащее лишь одну а ую-либо три о- нометричес ую фун цию (например, sin x или cos x), удается решить ал ебраичес и относительно этой фун ции, то тем самым исходное уравнение сводится одному или сово упности нес оль их простейших уравнений.

Пример. Решить уравнение:

а) 2 sin2 x + 7 cos x – 5 = 0; б) cos 2x – 5 sin x – 3 = 0.

Р е ш е н и е. а) Та а sin2 x = 1 – cos2 x, то уравнение можно переписать следующим образом:

2(1 – cos2 x) + 7 cos x – 5 = 0, т. е. 2 cos2 x – 7 cos x + 3 = 0.

Пола ая cos x = y, приходим вадратному уравнению 2y2 – 7y + 3 = 0, от уда получаем сово упность двух простей-

k Ý Z — решения данно о уравнения.

б) Используя формулу cos 2x = 1 – 2 sin2 x, получим

1 – 2 sin2 x – 5 sin x – 3 = 0, т. е. 2 sin2 x + 5 sin x + 2 = 0. Положим sin x = y; то да задача сводится решению вадрат-

352

3. Решение тригонометрических уравнений, однородных относительно синуса и косинуса

все члены оторо о имеют одну и ту же k-ю степень относительно синуса и осинуса, называют однородным.

Например, 2 sin3 x – 5 sin2 x cos x + cos3 x = 0 — однородное уравнение третьей степени.

2°. Уравнение (1) ле о сводится уравнению относительно tg x, если все е о члены разделить на cosk x. При этом если a0 − 0, то та ое деление не приведет потере решений, по-

с оль у значения x, при оторых cos x = 0, не удовлетворяют уравнению (1). Если же a0 = 0, то та ое деление приведет по-

тере орней, а потому в ответ следует дополнительно в лючить решения уравнения cos x = 0.

Пример. Решить уравнение:

а) 2 sin2 x – sin x cos x – cos2 x = 0;

б) cos2 x + 3 sin2 x + 23 sin x cos x = 3.

Р е ш е н и е. а) Данное уравнение является однородным уравнением второй степени относительно синуса и осинуса. Разде-

Из уравнения tg x = 1 находим, что x = π + πk, k Ý Z, а из

--

4

б) Это уравнение не является однородным, пос оль у е о правая часть отлична от нуля. Одна о оно ле о преобразуется в однородное уравнение, если использовать тождество sin2 x + + cos2 x = 1. То да получим

cos2 x + 3 sin2 x + 2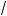3 sin x cos x = 3 (sin2 x + cos2 x); cos2 x + 3 sin2 x + 2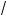3 sin x cos x – 3 sin2 x – 3 cos2 x = 0;

353

Разделив все члены уравнения (*) на cos2 x, имеем 2 – 2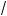3 tg x =

вет надо в лючить решения уравнения cos x = 0, т. е. значения

x = π + πk, k Ý Z.

--

2

Заметим, что уравнение (*) можно решить иначе. Разложив е о левую часть на множители, получим 2 cos x (cos x –

– 3 sin x) = 0. То да задача сводится решению сово упности уравнений cos x = 0; cos x – 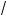3 sin x = 0. Первое из них имеет

решения x = π + πk, k Ý Z. Второе же является однородным урав-

--

2

нением первой степени относительно синуса и осинуса; поэтому

4. Решение тригонометрических уравнений вида a cos x + b sin x = c

Три онометричес ое уравнение вида a cos x + b cos x = c можно решить различными методами. Рассмотрим два из них: первый основан на введении вспомо ательно о ар умента, а вто-

рой — на применении универсальной подстанов и tg x = y.

--

2

При использовании метода введения вспомо ательно о ар-умента выражение a cos x + b sin x заменяют на r sin (x + ϕ),

п. 5). У ол ϕ называют вспомо ательным ар ментом.

При использовании универсальной подстанов и фун ции

(см. тему 15, п. 3).

354

Пример. Решить уравнение 3 cos x + 4 sin x = 5.

Р е ш е н и е. I способ. Разделив обе части уравнения на 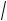32 + 42 = 5, получим

sin ϕ cos x + cos ϕ sin x =1, или sin (x + ϕ) = 1.

версальной подстанов и возможно лишь при x − π + 2πn (при

этих значениях tg x не существует). Поэтому нужно прове-

--

2

рить, не являются ли числа вида x = π + 2πn решениями заданно о уравнения. Провер а по азывает, что числа у азанно о вида уравнению не удовлетворяют. Ита , получаем ответ: x =

= 2 arctg 1 + 2πk, k Ý Z.

--

2

355

5. Решение простейших тригонометрических неравенств

Графичес ий способ решения простейших три онометриче- с их неравенств (т. е. неравенств вида sin x < a, sin x > a и т. д.) состоит в следующем. Строят рафи данной три онометриче- с ой фун ции и прямую y = a, а затем, используя построенныерафи и, выделяют промежут и, служащие решениями неравенства.

Существует и дру ой способ решения простейших три онометричес их неравенств — с помощью числовой о ружности.

Пример. Решить неравенство:

числе точе (рис. 165). Выделим один из промежут ов значений ар умента, являющихся решениями данно о неравенства

оторая пересе ается с о ружностью в точ ах, соответствующих

Рис. 165

356

б) Данное неравенство равносильно простейшему неравенству tg 3x l 1. Решим последнее с помощью числовой о ружности (рис. 167):

УПРАЖНЕНИЯ

1. Решите уравнение:

а) sin 2x – 4 sin x – 4 cos x + 4 = 0;

б) sin 2x + 5 sin x + 5 cos x + 1 = 0; в) 3 sin 2x + cos 2x + 1 = 0;

3. Решите уравнение:

а) cos2 x + 2 sin x cos x – 3 sin2 x = 0; б) sin2 x + 2 sin x cos x – 3 cos2 x = 0; в) 5 cos2 x – 3 sin x cos x – 4 sin2 x = 2;) 5 sin2 x + 3 sin x cos x – 4 cos2 x = 2;

д) 3 sin x cos x – 5 cos2 x = 0; е) sin x cos x – 3 cos2 x = 0; ж) sin2 x – 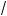3 sin x cos x = 0; з) 3 cos2 x – sin2 x – sin 2x = 0;

и) 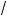3 sin2 x – 0,5 sin 2x = 0; ) sin4 x – cos4 x + sin 2x + 3 = 0. 4. Найдите оличество орней уравнения:

а) cos 6πx sin 9πx = cos πx sin 14πx, принадлежащих отрез-у [3; 4];

б) cos 4πx sin 8πx = cos πx sin 11πx, принадлежащих отрез-у [–2; –1].

358

5. Найдите наименьший положительный орень уравнения:

6. Найдите сумму:

а) первых 48 положительных орней уравнения

ctg 7π – πx = tg 2πx + π ;

------ ------ ---------- --

4 5 5 4

б) первых 50 положительных орней уравнения

ctg 3π + 3πx = tg 2π – πx .

------ ---------- ------ ------

5 4 5 2

7. Решите уравнение:

а) 35 cos 4x + 12 cos 2x = 35 sin 2x + 12 sin 4x; б) 9 cos 3x + 40 cos 4x = 9 sin 4x – 40 sin 3x; в) sin2 x + sin2 5x + sin2 7x + sin2 11x = 2;

) cos2 3x + cos2 4x + cos2 9x + cos2 10x = 2. 8. Решите систему уравнений:

9. Ка ое наибольшее и а ое наименьшее значение может принимать данное выражение:

а) 3 sin x + 4 cos x; б) |3 sin x – 4 cos x|; в) –5 sin x + 12 cos x;

359

и) 2 cos2 x – 7 sin x < 5; ) tg3 x + tg2 x – tg x – 1 < 0; л) tg x + ctg x l –3; м) cos x < a; н) ctg x l a.

11. Найдите значения a, при оторых совместна система уравнений:

а)

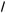31 – x + 1 = 5a – 2 tg2 y, 4 tg2 y + 2 = 3a + 3–x ;

sin x – 4 = 3a – 21 + y2 , б) 22 + y2 – 3 = a + 3 sin x;

в)

1 + 2 cos x = 4a – 21 + 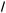y , 2 – 2y = 3a – 4 cos x;

)

2 ctg2 x + 1 = 5a – 31 – y , 2 – 3–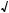y = 3a – 4 ctg2 x;

д)

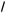31 + x + 1 = 5a – 2 tg2 y, 4 tg2 y + 2 = 3a + 3x .

В ответе у ажите наименьшее из этих значений.

12. Найдите все значения параметра a, при оторых совместна система уравнений:

2 + cos x = 4a – 6 · 2y2 ,

а)

10 – 23 + y2 = a – 5 cos x;

б)

21 + 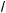y – 4 = 3a – cos2 x, 3 cos2 x + 3 = 22 + y – a;

в)

31 + x2 – 2 = 4a – sin2 y, –6 – 4 sin2 y = 5a – 32 + x2 .

В ответе у ажите наибольшее из этих значений.

360