Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Готовимся к экзамену по математике_Крамор В.С_2008 -544с

.pdf

Скачиваний:

482

Добавлен:

26.03.2016

Размер:

7.3 Mб

Скачать

☆

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 4344 / 5544 45 46 47 48 49 50 51 52 53 54 55 > Следующая >>>

7. Промежут и зна	опостоянства:
а) y > 0 при x Ý (–×; –1)			1	; +×	;
а) y > 0 при x Ý (–×; –1)			--	; +×	;
			2
б) y < 0 при x Ý –1;	1	.
б) y < 0 при x Ý –1;	--	.
	2
8. Найдем производную: y′ =				3
8. Найдем производную: y′ =				--------------------- . Э стремумов нет; фун ция
				(x + 1)2

возрастает на (–×; –1) и на (–1; +×).

К упражнению 9

1.Область определения D(y): x Ý R, x − 0.

2.Множество значений E(y): y Ý (1; +×).

3. Фун	ция четная, та а y(–x) = y(x).
4. Фун	ция непериодичес ая.

5. Корней нет, та а	x4	+ 1	− 0.
	------x----4------

6.Промежут и зна опостоянства: y > 0 при всех x Ý D(y).

7.Найдем производную:

y′ =	1	′	4
y′ =	-1 + ----- -		= –----- .
	x4		x5

Э стремумов нет; фун ция возрастает на (–×; 0) и убывает на (0; +×).

8. Графи фун ции изображен на рис. 195.

К упражнению 10а

1. Найдем производную данной фун ции:

y′ = -	(---x-----–-----1----)--2- ′	= 2----(---x-----–-----1----)---(--x----2----+------1----)---–-----(---x-----–-----1----)--2-------2----x--
	x2 + 1	(x2 + 1)2

2. Приравняв производную нулю, найдем фун ции:

Рис. 195

= 2(x – 1)(x + 1) .

-----------------------------------------

(x2 + 1)2

ритичес ие точ и

	2----(---x-----–-----1----)---(--x-----+------1----) = 0, от уда x			1	= –1, x	2	= 1.
	(x2 + 1)2
Эти точ и принадлежат заданному отрез у.
3.	Вычислим значения фун ции в		ритичес их точ ах и на он-
цах заданно:о отрез		а: y(–1) = 2, y(1) = 0, y(–2) = 1,8, y(2) = 0,2.
4.	Ита , max	y(x) = yнаиб = y(–1) = 2.
	x Ý [–2; 2]

431

К упражнению 11в

1.Найдем D(y): x Ý R, x − 0.

2.Найдем производную:

	y′ =	x2		1		′		1	x3 – 1
	y′ =		- -----	+ --	-		= x – ----- =		---------------- .
			2	x				x2	x2
3.	Приравняв производную нулю, получим x = 1 — ритичес ую
точ у, оторая принадлежит заданному отрез у [0,5; 2].
4.	Вычислим значения фун ции в							ритичес ой точ е и на онцах
отрез	а: y(1) = 1,5, y(0,5) = 2,125, y(2) = 2,5.
5.	Ита , min	y(x) = yнаим = y(1) = 1,5.
	x Ý [–0,5; 2]

К упражнению 12а

1.Найдем D(y): x > 0.

2.Запишем данную фун цию в виде y = x–1/2 – 2x–1 и найдем ее производную:

1	x–3/2	1	x–2(–x1/2	+ 4) =
y′ = (x–1/2 – 2x–1)′ = –--	x–3/2	+ 2x–2 = --	x–2(–x1/2	+ 4) =
2		2

4 – x .

-----------------

2x2

3. Критичес ую точ у фун ции найдем из уравнения								4 –	x	= 0,
3. Критичес ую точ у фун ции найдем из уравнения								-----------------		= 0,
								2x2
от уда x = 16.
4. Вычислим значения фун ции в							ритичес ой точ е и на		онцах
заданно:о отрез		а:
а) y(16) =	1	–	2	=	1	= 0,125;
а) y(16) =	--	–	------	=	--	= 0,125;
	4		16		8
1		2	= 0;
б) y(4) = --	– --		= 0;
2		4
в) y(25) =	1	–	2	=	3	= 0,12.
в) y(25) =	--	–	------	=	------	= 0,12.
	5		25		25
5. Значит,		max			y(x) = 0,125,		min y(x) = 0.
	x Ý [4; 25]					x Ý [4; 25]

6. Остается найти модуль разности наименьше:о и наибольше:о значений фун ции: |0 – 0,125| = 0,125.

К упражнению 13а

1.Найдем D(y): x Ý R.

2.Найдем производную и ритичес ие точ и данной фун ции. Имеем

y′ = (ax2 + 2ax – a2 + 1)′ = 2ax + 2a; y′ = 0 при x = –1.

432

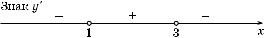
3. Следовательно,	нужно определить та ое a, чтобы	значение
фун ции в ритичес	ой точ е x = –1 было равно (–1). Та	а y(–1) =
= a(–1)2 + 2a(–1) – a2 + 1 = –a2 – a + 1, то получаем уравнение
–a2 – a + 1 = –1, или a2 + a – 2 = 0,
от уда a1 = –2, a2 = 1.
4. Со:ласно условию, данная фун ция в точ е x = –1 имеет ма си-

мум, поэтому оэффициент при x2 должен быть отрицательным, от у- да следует, что a = –2.

	К упражнению 14а
	1.	Зная x0 = 1, найдем ординату точ			и асания:
		y	0	= 3 · 13 – 4 · 12 + a2 · 1 + a = a2 + a – 1.
	2.	Находим производную данной фун ции:
		y′(x) = (3x3 – 4x2 + a2x + a)′ = 9x2 – 8x + a2,
от	уда y′(1) = a2 + 1.
	3.	Запишем уравнение асательной в точ				е (x0; y0) с учетом то:о,
что эта асательная проходит через точ					у A(2; 1). Имеем
				y = y0 + y′(x0)(x – x0),
или
		1 = a2 + a – 1 + (a2 + 1)(2 – 1),			т. е.	2a2 + a – 1 = 0,
от	уда a1 = –1, a2 = 1-- .
				2
	К упражнению 15а
	1.	Найдем производную данной фун ции:
	y′ = (---6----x-----–-----10--------)--(---x---2-----–-----4----x-----+------5----)---–-----(---2----x-----–-----4----)--(---3----x----2----–-----10-------x--------+---11--------) = --–-----x----2----+------4----x-----–-----3--- .
				(x2 – 4x + 5)2		(x2 – 4x + 5)2
	2. Приравняв производную нулю получим уравнение –x2 + 4x – 3 =

= 0, имеющее орни x1 = 1, x2 = 3. Эти числа разбивают числовую пря-

мую на три промежут а, в оторых зна и y′ изменяются та , а поазано на рис. 196.

3. Та им образом, минимум фун ции дости:ается в точ е с абсциссой x = 1. Ита , ymin = y(1) = 2.

Рис. 196

433

К упражнению 16а
1.	Сначала найдем производную данной фун ции:
		y′ =	–------x----8----+-----x----4----–------3--------7-- ′ = –2x7					+ x3.
					4
2.	Теперь определим у:ловой					оэффициент		асательной в точ е с
абсциссой x = 1:
					y′(1) = –2 + 1 = –1.
К упражнению 16в
1.	Нам известна ордината точ					и	асания: y = 0. Чтобы найти абс-
циссу этой точ и, решим уравнение
	0 =	x16 + 28x8		,	или x8(x8		+ 28) = 0, от уда x = 0.
	0 =	------------16-----------------		,	или x8(x8		+ 28) = 0, от уда x = 0.
		------------16-----------------
2.	Находим производную данной фун ции:
		y′ =	x----16-------+------28-------x----8-			′ = 16--------x----15-------+-----224-----------x----7- .
					16		16
3.	Найдем у:ловой				оэффициент		асательной в точ е с абсциссой
x = 0; имеем y′(0) = 0.

К упражнению 17б

1. Найдем нули фун ции y = (2x2 – 4x + 3)(x + 2):

а) 2x2 – 4x + 3 = 0 — это уравнение не имеет орней, та а D < 0; б) x + 2 = 0, от уда x = –2.

2. Найдем производную данной фун ции:

y′ = (4x – 4)(x + 2) + (2x2 – 4x + 3) · 1 = 6x2 – 5.

3. Теперь вычислим значение производной при x = –2:

y′(–2) = 6 · (–2)2 – 5 = 19.

К упражнению 18а

1. Сначала решим данную систему неравенств:

9	l 1,		x – 6	m 0,		x – 6	m 0,
9			-------------	m 0,		-------------	m 0,
x + 3		или	x + 3		или	x + 3
x + 3			x + 3			x + 3
			x − –3,			x − –3,
\|x – 4\| m 3,

			–3 m x – 4 m 3,			1 m x m 7.

С помощью числовой прямой (рис. 197) находим, что 1 m x m 6.

434

2. Ита , мы установили, что данная система неравенств имеет решение на отрез е [1; 6]. Теперь нужно определить наименьшее значение заданной фун ции на этом отрез е.

3. Находим производную:

				Рис. 197
y′ =	27	′	27	;
y′ =	3x + ------		= 3 – ------	;
	x		x2

уравнение y′ = 0 имеет	орни x1 = –3, x2 = 3. Отрез у [1; 6] принадле-
жит толь о орень x =	3.

4. Вычислим следующие значения: y(3) = 18, y(1) = 30, y(6) = 22,5. Ита , получаем ответ: 18.

К упражнению 25

1. У:лом между прямой и ривой называют у:ол между этой прямой и асательной ривой в точ е их пересечения (рис. 198).

2. Пусть ϕ — ис омый у:ол; то:да ϕ =

π	– α, :де α — у:ол, образуемый асатель-
= --	– α, :де α — у:ол, образуемый асатель-
2
ной с осью Ox.
	3.	Найдем производную фун ции y = x2;
имеем y′ = 2x.
	4.	Та	а tg α = y′(2) = 2 · 2 = 4, то α =
= arctg 4.
	5.	Ита	π
	5.	Ита	, ϕ = -- – arctg 4.
			2

К упражнению 26

1. Пусть R — радиус полу ру:а (рис. 199); то:да длина полуо ружности равна πR, нижнее основание прямоу:ольни а равно 2R, а

е:о бо овая сторона равна			1	(P		– 2R – πR).
е:о бо овая сторона равна			--	(P		– 2R – πR).
			2
2. Площадь о на выразится фун цией
1	– 2R –					1	π R	2	=
S(R) = 2R · -- (P	– 2R –		πR) + --				π R		=
2						2
= PR –		π		R	2	.
= PR –		2 + --		R		.
		2

Рис. 198

Рис. 199

435

Та а S(R) —

вадратичная фун ция, а оэффициент при R2

отрицателен, то она имеет точ у ма

симума.

Находим производную фун ции S(R):

S′(R) = (PR –

2 +

′

= P – (4 + π)R;

2--

S′(R) = 0

при

R =

-----P--------

4 + π

Отсюда следует, что

-- (P – (2 + π)R) =

1--

P –

2------+-----π--

P =

1--

P ·

4------+-----π-----–-----2-----–-----π--

-------------

= R,

4 + π

т. е. основание прямоу:ольной части о на должно быть вдвое больше е:о бо овой стороны.

К упражнению 27

1. Пусть x — сторона основания призмы; то:да площадь основа-

ния призмы равна S =	x2	3	.
ния призмы равна S =	------4------	-	.
	------4------
2. Объем призмы равен			V =	Hx2		3	, :де H — высота призмы. Зна-
2. Объем призмы равен			V =	---------	4---------	-	, :де H — высота призмы. Зна-
					4---------
чит, H = ----4----V----- .
x2 3
3. Полная поверхность призмы выразится та :
S(x) = 2 ·	x2	3	+ 3x ·		4V		=	x2 3	+	4V 3	.	(1)
S(x) = 2 ·	------4-----	--	+ 3x ·		x----2----	-----	=	------2-------	+	-------x--------	.	(1)
	------4-----				x----2----	3		------2-------		-------x--------

4.Нам нужно определить наименьшее значение фун ции (1) на (0; +×).

5.Найдем производную фун ции (1):

S′(x) = x 3 – 4V3 .

---------------

Имеем S′(x) = 0 при x3 = 4V, т. е. x = 3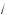4V — ритичес ая точ а фун ции S(x).

6. Та а S(x) убывает на (0; 3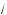4V ) и возрастает на (34V ; +×), то при x = 34V фун ция S(x) имеет минимум. Ита , ис омая сторона основания призмы равна 3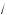4V .

436

К упражнению 28

1. Расстояние между ис омой точ ой B(x; x2), лежащей на параболе (рис. 200), и данной точ ой A(2; 0,5) выразится формулой

r(x) = (x – 2)2 + (x2 – 0,5)2 .

Рис. 200

2. Рассмотрим фун цию f(x) = r2(x) = (x – 2)2 + (x2 – 0,5)2; та а фун ция r(x) положительна при всех x, то минимумы этих фун ций должны дости:аться при одном и том же значении x.

3. Найдем производную фун ции f(x):

f′(x) = 2(x – 2) + 2(x2 – 0,5) · 2x = 4x3 – 4 = 4(x3 – 1).

4.Имеем f′(0) = 0 при x = 1, причем если x < 1, то f′(x) < 0, а если x > 1, то f′(x) > 0. Отсюда следует, что x = 1 — точ а минимума фун - ции f(x), а, значит, и фун ции r(x).

Ответ: (1; 1).

К упражнению 29а

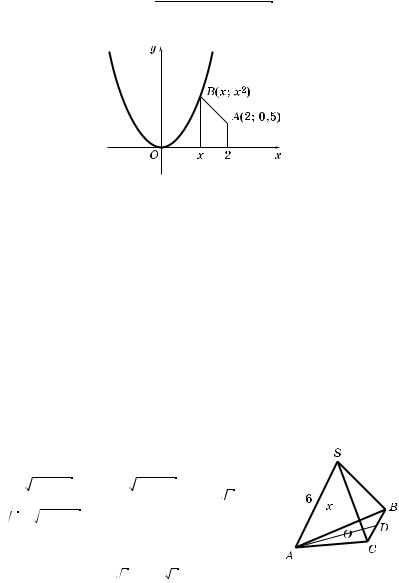
1. Дана правильная треу:ольная пирамида SABC (рис. 201), у оторой SA = 6.

2. Пусть SO = x — высота пирамиды. То:да
2. Пусть SO = x — высота пирамиды. То:да
OA = 36	3		2
OA = 36	– x2 , AD = --	36 – x2 , AC = ------- AD =
	2		3
= 3 · 36 – x2 .
3. Запишем фун цию, выражающую объем


пирамиды:
1	3	3	(36x – x3).
V = --	· 3(36 – x2)-------	· x = -------	(36x – x3).
3	4	4	Рис. 201

437

4. Найдем производную этой фун ции:

3	(36 – 3x2);
V′ = -------	(36 – 3x2);
4

из равенства V′ = 0 следует, что x = 23 . Ле: о убедиться в том, что это точ а ма симума фун ции V.

5. Остается вычислить наибольшее значение объема:

V	3	(72 3 – 24 3 ) = 36.
V	= -------	(72 3 – 24 3 ) = 36.
max	4

К упражнению 30

1.Пусть v ( м/ч) — с орость автобуса при старом расписании; то:да v + 10 ( м/ч) — е:о с орость при новом расписании.

2.Пусть t (ч) — время движения автобуса при старом расписании;

2
то:да t – -- (ч) — время е:о движения при новом расписании.
3
3. Используя формулу s = vt, составим систему
	vt = 325,					v =	325		,
							325
							---------
							t
		2		т. е.
	(v + 10) t – --		= 325,				2		20
	(v + 10) t – --		= 325,				2		20
		3				vt – --		v + 10t – ------		= vt,
							3		3
от уда получаем уравнение
			3t2 – 2t – 65 = 0.
Оно имеет орни t1 = 5, t2				13	(не подходит по смыслу задачи).
Оно имеет орни t1 = 5, t2				= –------	(не подходит по смыслу задачи).
				3

Значит, t = 5 (ч).

4. Теперь находим v = 325 : 5 = 65 ( м/ч), от уда v + 10 = 75 ( м/ч).

К упражнению 32а

1. Требуется решить систему

		2cos	2π	+ 4cos	π				(1)
			2π		π
			------		-- – 1 = 0,
			x		x
		4	l 5.						(2)
		4
		-------------
		1 – x
2. Находим область определения системы:
	x − 0,


	1 – x − 0,			т. е.	x − 0, x − 1.
	1 – x − 0,			т. е.	x − 0, x − 1.
3. Решим неравенство (2):
4	m 0, или			5x – 1	m 0, т. е. x Ý			; 1	.
4				5x – 1			1
5 + -------------				-----------------		--
x – 1				x – 1			5

438

4. Та им образом, решением системы являются

орни уравне-

ния (1), принадлежащие промежут у

; 1 .

5. Теперь решим уравнение (1). Имеем

2cos

2π

– 3 = 0.

(3)

------

+ 4cos -- – 1 = 0, или

4cos2 --

+ 4cos --

Найдем орни уравнения (3):

= –

(не подходит);

а) cos --

;

б) cos --

= ä-- + 2πk, k Ý Z;

= ä--

+ 2k, k Ý Z; x = ---------------- .

6k ± 1

6. Из этих значений промежут у

; 1 принадлежат: -- ;

------

; -- ;

------ .

К упражнению 33а

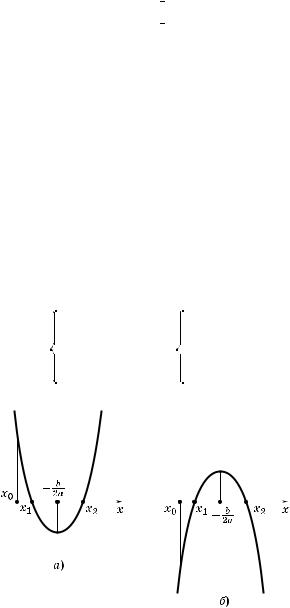
1. Та

оба

орня вадратно:о уравнения должны быть больше

заданно:о числа x

= -- , то в силу известной теоремы (см. тему 9, п. 5,

теорему 3) должны выполняться следующие условия (рис. 202, а и б):

	a > 0,				a < 0,
	D l 0,				D l 0,
а)	b	> x	,	или б)	b	> x	,
	–------	> x	,		–------	> x	,
	2a	0			2a	0
	f(x0) > 0				f(x0) < 0.

Рис. 202

439

2. Решим систему а):
		2 – k > 0,					k < 2,
		2 – k > 0,					k < 2,
		9k2 – 8k(2 – k) l 0,					k(17k – 16) l 0,
		3k	1	,	или		2k – 1		> 0,
		3k	1
	--------------------- >		--			----------------
		2( 2 – k)	2				2 – k
		2( 2 – k)	2
		1	3				1	k
		1	3	k + 2k	> 0,			+ --	> 0,
		-- (2 – k) –	--	k + 2k	> 0,		--	+ --	> 0,
		4	2				2	4
16	m k < 2.
от уда ------	m k < 2.
17
3. Решим систему б):
		2 – k < 0,					k > 2,
		2 – k < 0,					k > 2,
		9k2 – 8k(2 – k) l 0,					k(17k – 16) l 0,
		3k	1	,	или		2k – 1		> 0,
		3k	1
	--------------------- >		--			----------------
		2( 2 – k)	2				2 – k
		2( 2 – k)	2
		1	3				1	k
		1	3	k + 2k	< 0,			+ --	< 0.
		-- (2 – k) –	--	k + 2k	< 0,		--	+ --	< 0.
		4	2				2	4
		4	2

Эта система не имеет решений.

Ответ: 16 m k < 2.

------

К упражнению 34а

1. Рассмотрим три случая: cos x = 0, cos x > 0, cos x < 0.

2. Если cos x = 0, то x = π + πk; здесь при любых k Ý Z мы не полу-

чим ни а их целых орней.

3. Если cos x > 0, то 2x2 – 4x – 23 – 7 = 0, или x2 – 2x – 15 = 0, отуда x1 = –3, x2 = 5. Но cos (–3) < 0, а cos 5 > 0, т. е. x = 5 есть орень

уравнения.
4.	Если cos x < 0, то 2x2 – 4x – 23 + 7 = 0, или x2 – 2x – 8 = 0, от у-
да x1 = –2, x2 = 4. Та			а cos (–2) < 0 и cos 4 < 0, то x = –2 и x = 4 яв-
ляются орнями уравнения.
5.	Найдем сумму целых орней: 5 – 2 + 4 = 7.
К упражнению 35а
1.	Данное неравенство равносильно системе
		x2 – 2x – 8 l 0,			x2 – 2x – 8 l 0,
					x2 – 2x – 8 l 0,
				или	6 – x > 0,

		log	(6 – x) l 0,
		0,5			6 – x m 1.
		0,5			6 – x m 1.

2.Решив эту систему, находим x Ý {–2} {4} [5; 6).

3.Сумма целых решений есть –2 + 4 + 5 = 7.

440

<<< < Предыдущая 31 32 33 34 35 36 37 38 39 40 41 42 4344 / 5544 45 46 47 48 49 50 51 52 53 54 55 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.05.2015121.34 Кб8Глава 3.doc
#
31.05.2015262.14 Кб5Глава 4.doc
#
26.03.201634.51 Кб69Голубь задачи.docx
#
31.05.2015102.4 Кб8ГОС.РТ.doc
#
31.05.20151.48 Mб3ГОСТ 91.doc
#
26.03.20167.3 Mб482Готовимся к экзамену по математике_Крамор В.С_2008 -544с.pdf
#
31.05.2015243.71 Кб116грам.стил.doc
#
31.05.201520.85 Кб39гтн25.docx
#
31.05.20153.6 Mб66Деревянко_БС ЭВМ.pdf
#
31.05.20151.34 Mб57дип20.docx
#
31.05.20151.08 Mб95Диплом .doc