
2 |
π sin |
|
π |
|
удовлетворяет уравнению |
) y = -- |
|
x + -- |
|
3 |
|
3 |
|
log |
|
|
1 |
|
3 |
|
= 1 – 0,5 log |
|
(ctg y – tg y). |
|
---------------- – |
--------- |
|
|
|
4 |
ctg 2y |
tg y |
|
|
|
|
|
|
2 |
|
|
|
13. До ажите, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) arcsin x + arccos x = |
π |
; |
|
|
|
|
|
|
|
|
|
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
б) 2arctg |
1 |
+ arctg |
|
1 |
|
|
|
32 |
; |
|
|
|
|
|
|
|
-- |
|
-- |
= arctg ------ |
|
|
|
|
|
|
|
|
|
5 |
|
|
4 |
|
|
|
43 |
|
|
|
|
|
|
|
|
в) arccos |
1 |
+ arccos |
|
– |
1 |
= arccos |
|
– |
13 |
; |
-- |
|
-- |
|
|
------ |
|
|
|
2 |
|
|
|
7 |
|
|
|
|
14 |
|
) arcsin |
9 |
|
|
4 |
= –arcsin |
84 |
|
|
|
|
------ |
– arccos -- |
--------- . |
|
|
|
|
|
41 |
|
|
5 |
|
|
|
|
205 |
|
|
|
|
Задания для повторения
14.Из полно о ба а, содержаще о 729 л чистой ислоты, вылили k литров ислоты и долили ба водой. После перемешивания (до получения однородно о раствора) из ба а вылили k литров раствора, затем долили ба водой и перемешали. После то о а та ая операция была проделана 6 раз, жид ость в ба-е содержала 64 л чистой ислоты. Определите значение k.
15.В сосуде было 10 л соляной ислоты. Часть соляной ислоты отлили, а сосуд дополнили та им же оличеством воды. Затем снова отлили та ое же оличество смеси и долили та ое же оличество воды. С оль о литров отливали аждый раз, если
врезультате в сосуде о азался 64%-ный раствор соляной ислоты?
16.Найдите сумму 20 членов арифметичес ой про рессии, если ее 1-й член равен 2, а 7-й член равен 20.
17.Сумма 1- о и 5- о членов арифметичес ой про рессии равна 26, а произведение 2- о и 4- о ее членов равно 160. Найдите сумму первых шести членов про рессии.
18.Три числа, аждое из оторых является степенью с основанием a (a > 0, a − 1), составляют еометричес ую про рессию. До ажите, что ло арифмы этих чисел образуют арифметичес ую про рессию.
19.Найдите знаменатель и сумму бес онечно убывающей
|
еометричес ой про рессии, в оторой b1 = 3 , b2 = |
2 |
. |
|
3-----+-----1-- |
|
|
|

20. До ажите справедливость неравенства:
а) tg x + ctg x l 2, если 0 < x < π ;
--
2
б) 2 sin 4α sin 2α + cos 6α l –1.
О Т В Е Т Ы
2. а) – |
-π- |
; б) 5----π-- |
; в) –--7---- |
; $) 1-- ; д) 2---------2- ; е) |
3----π-- |
; ж) -π- |
; з) – |
--π---- |
; и) |
-π- |
; |
|
|
8 |
|
14 |
|
25 |
|
5 |
3 |
4 |
5 |
|
|
14 |
|
5 |
|
) – -π- |
; л) |
-π- |
; м) –2---- |
π-- . 3. а) –× < x m –3, –1-- m x < +×; б) – |
2-- |
m x m |
4-- |
; |
3 |
|
4 |
|
5 |
|
|
|
2 |
|
|
|
3 |
|
|
3 |
|
в) – |
2 m x m |
2 ; $) –× < x < –3, –3 < x < 3, 3 < x < +×; д) –× < x m 2, |
3 m x < +×. 4. а) 1; б) 63------ |
в) 2-- ; $) – 56------ ; д) 8---------3- ; е) |
--8---- ; ж) 4---------7-----–-----3-- |
; з) ----- |
5-- |
; |
|
|
|
|
|
65 |
|
9 |
65 |
49 |
|
17 |
10 |
2 |
20 |
|
и) 24------ |
; ) 2x2 – 1; л) -----2----x------- |
. 5. а) Один орень; б) пять орней; в) три |
25 |
|
|
|
|
1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
орня; $) три |
орня; |
д) три |
орня; |
е) три |
орня; |
ж) два |
орня. |
6. а) 855°; б) 405°; в) 990°; $) 720°; д) 675°; е) 855°; ж) 840°. 7. а) –3; б) 0,75; в) 2; $) 0; д) 1. 8. а) 12π; б) шесть орней; в) три орня; $) два
орня; д) пять орней; е) –225°. 9. а) –
 2 m a m
2 m a m 
 2 ; б) –0,5 m a m 1,5;
2 ; б) –0,5 m a m 1,5;
в) x = 3π + 2πk, k Ý Z; x = π + (–1)karcsin (2a – 1) + πk, $де 0 m a m 1,
------ --
4 4
k Ý Z; $) если a Ý [–3; 5], то x = (–1)karcsin (
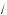 4 + a – 2) + πk, k Ý Z; в частности, если a = 0, то x = πk, k Ý Z; д) если a Ý [–4; 2], то x =
4 + a – 2) + πk, k Ý Z; в частности, если a = 0, то x = πk, k Ý Z; д) если a Ý [–4; 2], то x =
|
= äarccos |
3-----–----------9-----–-----4----a-- |
+ 2πk, k Ý Z; если a Ý (–×; –4) или a Ý (2; +×), |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то нет решений. 10. |
x = πk; x = πk ä |
|
|
1 |
|
|
– 1 + |
1 + 2a |
, k Ý |
Z. |
|
|
|
-- arccos |
----------------- |
-2-------- |
----------- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
11. а) x = (–1)karcsin 1-- |
+ πk, x = (–1)karcsin 5-- |
+ πk, x = (–1)k + 1 × |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
× arcsin 7-- |
+ πk, k Ý Z; б) x = äarccos |
--2---- |
|
+ 2πk, x = äarccos --6---- + 2πk, |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
11 |
|
|
x |
= äarccos |
|
– |
10 |
|
+ |
2πk, k |
Ý Z; |
в) x |
= äarccos |
7 |
+ 2πk, x |
= |
|
|
11------ |
|
9-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= äarccos |
|
– |
1 |
+ 2πk, |
x = |
äarccos |
|
– |
5 |
|
+ 2πk, |
k Ý Z; $) x |
= |
|
|
9-- |
|
9-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
n π |
|
|
= äarccos |
12------ |
|
+ 2πk, x = äarccos – |
12------ |
+ 2πk, k Ý Z. 12. а) x = (–1) 12------ |
+ |
|
+ |
π n |
, x = – |
π |
|
+ πn, n |
Ý Z; б) x = (–1)n + 1 |
π |
|
– |
π |
+ πn, x = |
π |
+ 2πn, n Ý Z; |
|
--2---- |
4-- |
|
-- |
|
3-- |
6-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|

в) x = (–1)n + 1 |
π |
π |
π |
+ 2πn, n Ý Z; $) x |
= (–1)n + 1 |
π |
π |
+ πn, |
-- |
– -- |
+ πn, x = -- |
-- |
– -- |
|
|
6 |
4 |
4 |
|
|
6 |
3 |
|
π |
+ 2πn, n Ý |
Z. 14. k = 243. 15. 2 л. 16. |
610. 17. 87 или 69. |
x = -- |
6 |
|
|
|
|
|
|
|
|
|
Решения и методичес ие у азания
К упражнению 1а
1.Фун ция четная, та а sin |–x| = sin |x|.
2.При x l 0 имеем sin |x| = sin x, т. е. на положительной полуоси Ox ривая является обы новенной синусоидой (сплошная линия на рис. 159); при x m 0, т. е. на отрицательной полуоси, получаем ривую, симметричную построенной относительно оси Oy (пун тирная линия на рис. 159).
К упражнению 1б
1.Найдем множество значений фун ции: –1 m –|sin x| m 0.
2.Значит, $рафи фун ции будет цели ом расположен ниже оси Ox.
3.Если sin x l 0, то y = –sin x. Следовательно, в промежут ах, $де
sin x l 0, $рафи будет тот же, что и $рафи фун ции y = –sin x (на рис. 160 эта часть ис омо$о $рафи а изображена сплошной линией).
4.Если sin x m 0, то y = sin x. Значит, часть $рафи а фун ции y =
=sin x, расположенная выше оси Ox, симметрично отразится относительно оси Ox и будет расположена под этой осью ( а по азано на рис. 160 пун тирной линей).
5.Из рисун а видно, что данная фун ция четная и периодичес ая с периодом π.
К упражнению 1
1.Фун ция четная, пос оль у tg |–x| = tg |x|.
2.Если x l 0, то y = tg x, следовательно, на положительной полуоси Ox $рафи тот же, что и $рафи фун ции y = tg x. На рис. 161 эта часть ис омо$о $рафи а изображена сплошной линией.
Рис. 161
3. Часть $рафи а при x m 0 симметрична построенной части и изображена на рис. 161 пун тирной линией.
К упражнению 1ж |
|
|
|
|
|
|
|
|
|
|
|
1. |
Фун ция определена на всей числовой прямой. |
|
2. |
Имеем y = cos x + cos |
π |
– x |
|
= |
2 sin |
|
π |
. |
|
-- |
|
|
x + -- |
|
|
|
|
|
2 |
|
|
|
4 |
|
|
3. |
|
π |
| m 1, то |
2 — ма симум фун ции, а – 2 |
Та а |sin x + -- |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
есть ее минимум. |
|
|
|
|
|
|
|
|
|
|
|
4. |
Период фун ции равен T = 2π. |
|
|
|
|
|
5. |
Корнями фун ции являются точ и x = |
π |
, k Ý Z. |
|
πk – -- |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
6. |
Графи фун ции получается растяжением синусоиды y = sin x |
|
|
|
|
|
|
|
|
|
|
π |
|
|
в 2 раз вдоль оси ординат и сдви$ом влево на -- . |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
7. |
Ис омый $рафи изображен на рис. 162. |
|
|
К упражнению 1з |
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
π |
+ πk, |
Та а tg x и sec x теряют смысл при cos x = 0, то x − -- |
2
k Ý Z. 324

4.Графи фун ции y = 3 + cos 2x можно построить иначе, если воспользоваться тем же исходным $рафи ом (y = cos 2x), но вместо переноса всей ривой на 3 ед. вверх перенести ось Ox на 3 ед. вниз.
5.Тем самым относительно новой оси Ox все ординаты ривой y =
=cos 2x увеличатся на 3 ед. и получится ис омый $рафи .
К упражнению 2а
1. Из определения ар тан$енса следует, что arctg (tg x) = x при ус-
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ловии –-- < x < -- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Поэтому нужно, чтобы выражение под зна ом тан$енса было |
за лючено в интервале |
|
π |
; |
π |
: |
|
|
|
|
|
|
|
–-- |
-- |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
arctg |
|
7π |
= arctg |
|
tg |
|
π |
= arctg |
|
tg |
|
π |
π |
|
tg ------ |
|
|
|
π – -- |
|
|
–-- |
= –-- . |
|
8 |
|
|
|
|
8 |
|
|
8 |
8 |
К упражнению 2б
1. Используя формулу приведения, получим
arccos |
|
|
15π |
= arccos |
|
sin |
|
|
|
π |
= arccos |
|
|
π |
. |
|
sin ---------- |
|
|
|
2π + -- |
|
|
sin -- |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
7 |
|
|
|
|
7 |
|
2. Теперь, |
чтобы |
|
воспользоваться |
формулой |
arccos (cos x) = x, |
|
|
|
|
|
|
π |
|
на осинус дополнительно$о у$ла: |
|
|
нужно заменить sin -- |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos |
|
|
|
π |
= arccos |
|
cos |
π |
– |
π |
= arccos |
|
|
5π |
5π |
|
sin -- |
|
|
|
-- |
-- |
|
|
cos ------ |
= ------ . |
|
|
|
7 |
|
|
|
|
2 |
|
|
7 |
|
|
|
|
14 |
14 |
К упражнению 2в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
, а cos α = |
1 – |
16 |
3 |
|
1. Пусть α = arcsin -- . То$да sin α |
= -- |
------ |
= -- . |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
25 |
5 |
|
2.Перед ради алом взят зна «плюс», та а по определению ар - синуса у$ол α лежит в I четверти, а осинус та о$о у$ла положителен.
3.Теперь вернемся данному выражению и получим
cos |
|
4 |
|
2 |
α – sin |
2 |
7 |
|
2 arcsin -- |
|
= cos 2α = cos |
|
α = –------ . |
|
5 |
|
|
|
25 |
К упражнению 2з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Пусть y = arctg ctg |
11--------π-- |
. То$да tg y = ctg |
11--------π-- |
, $де – |
|
-π- |
< y < |
-π- . |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
|
|
2 |
|
|
2 |
|
2. |
Упростив ctg 11--------π-- |
, получим ctg |
11-------π =--- tg |
3----π-- |
|
– |
11--------π-- |
= tg |
–--π---- |
. |
|
7 |
|
|
|
|
|
|
7 |
|
2 |
|
|
7 |
|
|
|
|
14 |
3. |
Та им образом, tg y = tg |
|
– |
π |
, т. е. y = – |
π |
. |
|
|
|
|
|
|
|
|
|
---- |
----- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
14 |
|
|
|
|
|
|
|
|
К упражнению 2и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Пусть α = arcsin |
|
sin |
4π |
. То$да sin α = sin |
4π |
, $де – |
π |
|
|
π |
. |
|
--5---- |
-- |
5---- |
2-- |
m α m -- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2. |
Отсюда нельзя за лючить, что α = 4π------ |
, пос оль у |
4----π-- |
|
> -π- . |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
2 |
|
|
|
3. |
Упростим sin 4----π-- ; имеем sin |
4----π-- |
= sin |
π – -π- |
= sin |
-π- . |
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
4. |
Та а sin 4----π-- = sin |
-π- , то sin α = sin |
-π- . Ита , α = |
-π- . |
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
К упражнению 3а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Та а y = arccos -2----x-----–-----1-- , то cos y = 2-----x-----–-----1-- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2 |
|
|
|
|
3x + 2 |
|
|
|
|
|
|
|
|
|
|
|
2. |
Задача сводится решению следующе$о двойно$о неравенства: |
|
|
|
|
|
|
|
|
|
2x – 1 |
m 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 m 2x – 1 |
m 1, |
|
или |
|
3x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2 |
|
|
|
|
|
-----------------2x – 1 |
l –1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
3. Решив систему |
неравенств, |
получим ответ: –× < |
|
x |
m –3, |
–1 m x < +×.
--
2
К упражнению 3 |
|
1. |
Задача сводится решению системы неравенств |
|
|
x |
< +×, |
|
|
|
|
–× < ---------------- |
|
|
x2 – 9 |
|
|
|
x2 – 9 − 0. |
|
|
|
|
2. |
Решением этой системы является множество всех действитель- |
ных чисел, роме x = –3 и x = 3. 328

3. С учетом введенных обозначений данное выражение примет вид cos (α + β) = cos α cos β – sin α sin β. (1)
4. Найдем cos α и sin α:
|
|
|
3 |
|
|
|
|
ctg α |
|
-- |
= 3 |
|
1 – cos2 α = 4 . |
а) cos α = --------- |
-- |
= -4-- |
; б) sin α = |
1 |
2 |
α |
5 |
5 |
|
5 |
+ ctg |
-- |
|
|
|
|
|
|
4 |
|
|
|
5. Найдем cos β и sin β:
а) cos β = ctg β |
|
–12------ |
= –12 ; |
|
|
|
|
|
|
|
|
---- = |
------5---- |
|
|
б) sin β = |
1 – cos2 β = --5---- . |
1 + ctg2β |
13------ |
|
|
|
13 |
|
|
|
|
|
|
|
13 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
6. Подставив в выражение (1) найденные значения три$онометри- |
чес их фун ций, получим |
|
|
|
|
|
|
|
|
|
|
|
|
cos (α + β) = |
3 |
|
– |
12 |
– |
4 |
· |
5 |
= – |
56 |
. |
|
5-- |
|
13------ |
5-- |
13------ |
65------ |
|
|
|
|
|
|
|
|
|
|
К упражнению 4ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Пусть arctg 1-- |
= α; то$да – |
-π- < α < |
|
-π- , tg α = |
1-- |
, т. е. α — у$ол |
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
I четверти. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Пусть arccos 3-- |
= β; то$да 0 < β < π, cos β = |
3-- |
, т. е. β — у$ол |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
Iчетверти.
3.Следовательно, данное выражение примет вид
|
sin |
|
2α – |
β |
= sin 2α cos |
β |
– sin |
β |
cos 2α. |
|
|
(1) |
|
|
2-- |
2-- |
2-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. В выражении (1) содержится у$ол |
-β- |
. Та а 0 < β < |
-π- , то 0 < |
-β- < |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
< -π- |
, т. е. -β- — у$ол I четверти. |
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Теперь по известным значениям tg α = |
1-- |
и cos β = |
3-- |
будем ис- |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
ать sin 2α, cos 2α, sin |
|
-β- и cos |
-β- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
6. Для нахождения sin 2α и cos 2α используем формулы синуса и |
осинуса двойно$о ар$умента: |
|
|
|
|
|
|
|
|
|
|
sin 2α = 2 tg α |
|
2 |
|
1-- |
= 4 , cos 2α = 1 – tg2 α |
1 – 1-- |
= 3 . |
|
|
= ------- |
--- |
2--- |
= ---------- |
-4-- |
|
|
1 + tg2 α |
|
1 + |
1 |
5 |
|
1 + tg2 α |
1 + |
1 |
5 |
|
|
|
|
|
|
4-- |
|
|
|
|
|
4-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|











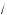 2 m a m
2 m a m 
 2 ; б) –0,5 m a m 1,5;
2 ; б) –0,5 m a m 1,5;
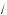 4 + a – 2) + πk, k Ý Z; в частности, если a = 0, то x = πk, k Ý Z; д) если a Ý [–4; 2], то x =
4 + a – 2) + πk, k Ý Z; в частности, если a = 0, то x = πk, k Ý Z; д) если a Ý [–4; 2], то x =