
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf3°. При основании 0 < a < 1 ло арифмы чисел N > 1 отрицательны, а ло арифмы чисел 0 < N < 1 положительны. Напри-
мер, log |
|
5 < 0; log |
|
1 |
> 0. |
0,5 |
0,5 |
-- |
|||
|
|
3 |
|
4°. Равным положительным числам соответствуют и равные ло арифмы, т. е. если N1 = N2, то loga N1 = loga N2.
5°. Если a > 1, то большему числу соответствует и больший ло арифм, т. е. если N1 > N2, то loga N1 > loga N2. Например,
log3 7 > log3 5.
6°. Если 0 < a < 1, то большему числу соответствует меньший ло арифм, т. е. если N1 > N2, то loga N1 < loga N2. Напри-
мер, log1/3 9 < log1/3 7.
7°. Ло арифм единицы по любому основанию (a > 0, a − 1) равен нулю, т. е. loga 1 = 0.
8°. Ло арифм само о основания равен 1, т. е. loga a = 1.
3. Логарифмическая функция, ее свойства и график
1°. Та а по азательная фун ция y = ax ( де a > 0, a − 1) является монотонной (возрастающей при a > 1 и убывающей при 0 < a < 1), то она имеет обратную фун цию. Чтобы найти эту обратную фун цию, нужно из формулы y = ax выразить x через y: x = loga y, а затем поменять обозначения x на y и y на x; то да получим y = loga x. Фун цию y = loga x ( де a > 0, a − 1)
называют ло арифмичес ой.
Ита , по азательная и ло арифмичес ая фун ции при одном и том же основании являются взаимно обратными фун циями.
2°. Графи ло арифмичес ой фун ции y = loga x можно построить, воспользовавшись тем, что фун ция y = loga x обратна по азательной фун ции y = ax. Поэтому достаточно построитьрафи фун ции y = ax, а затем отобразить е о симметрично относительно прямой y = x. На рис. 118 изображен рафи фун ции y = loga x при a > 1, а на рис. 119 — рафи фун ции y = loga x при 0 < a < 1.
3°. Отметим свойства фун ции y = loga x при a > 1:
а) D(f) = R+; б) E(f) = R;
в) фун ция возрастает;
211
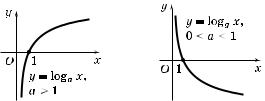
Рис. 118 |
Рис. 119 |
) x = 1 _ loga x = 0;
д) 0 < x < 1 _ loga x < 0; е) x > 1 _ loga x > 0.
4°. Отметим свойства фун ции y = loga x при 0 < a < 1:
а) D(f) = R+; б) E(f) = R;
в) фун ция убывает;) x = 1 _ loga x = 0;
д) 0 < x < 1 _ loga x > 0; е) x > 1 _ loga x < 0.
4. Теоремы о логарифме произведения, частного и степени. Формула перехода к новому основанию
1°. Ло арифм произведения двух или нес оль их положительных чисел равен сумме ло арифмов сомножителей, т. е.
loga (N1N2 ... Nk) = loga N1 + loga N2 + ... + loga Nk.
Например, loga (3 · 4 · 6 · 7) = loga 3 + loga 4 + loga 6 + loga 7.
2°. Ло арифм частно о положительных чисел равен разности ло арифмов делимо о и делителя, т. е.
|
log |
N1 |
= log |
|
N |
|
|
– log |
N |
. |
|||
|
------- |
a |
1 |
||||||||||
|
|
a N |
2 |
|
|
|
|
a |
2 |
|
|||
Например, log |
3 |
= log |
|
3 – log |
|
4. |
|
|
|||||
-- |
|
|
|
|
|||||||||
|
a 4 |
|
|
|
a |
|
|
|
|
a |
|
|
|
3°. Ло арифм степени равен произведению по азателя степени на ло арифм ее основания, т. е.
loga Nc = c loga N.
212
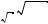
З а м е ч а н и е. Если N < 0, а c — четное число, то справедлива формула
Например, loga (–3)4 = 4loga |–3|.
4°. Формула перехода от основания b основанию a имеет вид
log N = logaN . b ----------------
logab
Например, log 7 = log47 = lg7 и т. д.
2 -------------- --------
log42 lg2
5°. Если a = N, то формула перехода примет вид
log |
b |
a = |
------1-------- , или 1 = log |
b |
a · log |
a |
b. |
|
|
logab |
|
|
|||
|
|
|
|
|
|
|
Например, 1 = log2 7 · log7 2.
6°. Если основание ло арифма и число, находящееся под зна ом ло арифма, возвести в одну и ту же степень, отличную от нуля, то значение ло арифма не изменится, т. е.
log N = log |
|
cNc ; |
|
log |
|
kN = log |
|
|
|
|
|
logaN |
|
|
|||||||||||||
|
|
|
|
|
N1/k = ---------------- . |
|
|
||||||||||||||||||||
a |
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
k |
|
|
|
Например, log |
|
4 = log |
|
3 43 ; |
log |
|
64 = log |
|
3 26 |
6 |
|
2 = 2. |
|||||||||||||||
2 |
|
8 |
|
= -- log |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 – -- log5 49 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Примеры. 1. Найти 25 |
4 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Р е ш е н и е. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 – |
1 |
|
|
|
|
|
|
|
|
|
1 – |
1 |
|
|
|
49 |
|
|
|
2 – |
1 |
49 |
|
|
|||
-- log5 49 |
|
|
|
|
-- log5 |
|
|
|
-- log5 |
|
|
||||||||||||||||
25 |
4 |
|
|
|
|
|
|
= (52) |
|
4 |
|
|
|
= |
|
5 |
2 |
. |
|
|
|||||||
Преобразуем теперь по азатель степени: |
|
|
|
|
|
||||||||||||||||||||||
2 – |
|
1 |
|
|
|
|
49 = 2log |
|
|
5 – log |
|
|
491/2 = |
|
|
|
|||||||||||
|
-- log |
5 |
5 |
5 |
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= log |
|
52 |
– log |
|
|
7 = log |
|
|
|
25 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
------ . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
5 |
|
7 |
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
25 |
25 |
|
|
|
|
|
|
|
|||
Следовательно, |
|
2 – |
-- log5 |
49 |
log5 |
------ |
|
(в силу основно о ло- |
|||||||||||||||||||
5 |
|
|
2 |
|
|
|
|
|
= 5 |
|
|
|
|
7 |
|
= ------ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
арифмичес о о тождества). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. Найти log |
4 |
|
8 |
243 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
213
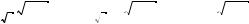
Р е ш е н и е. Основание ло арифма и ло арифмируемое число можно возвести в одну и ту же степень. Поэтому
log |
8 243 = log |
|
|
4(8 243) |
4 |
= log |
|
243 = log |
|
35/2 |
5 |
(4 |
|
|
3 |
3 |
= -- . |
||||||
|
4 3 |
3) |
|
|
|
|
|
2 |
3. Найти log30 8, если lg 5 = a и lg 3 = b. Р е ш е н и е. Имеем
log 8 = log 23 = 3 log 2 = 3 lg 2 ;
30 30 30 --------------
lg 30
lg 2 = lg 10 = lg 10 – lg 5 = 1 – a;
------
5
lg 30 = lg (2 · 15) = lg 2 + lg 15 = lg 2 + lg (3 · 5) = = lg 2 + lg 3 + lg 5 = 1 – a + b + a = 1 + b.
Ита , log 8 = 3(1 – a) .
30 ---------------------
1 + b
5. Десятичные логарифмы и их свойства
1°. Десятичный ло арифм числа — это ло арифм с основанием, равным 10; например, lg a, lg 5, lg 1. Десятичные ло-арифмы обладают теми же свойствами, что и ло арифмы чисел с любым положительным основанием.
2°. Десятичные ло арифмы чисел находят по специальным таблицам (ре омендуется использовать «Четырехзначные математичес ие таблицы» В. М. Брадиса).
3°. Целую часть десятично о ло арифма числа называют е о хара теристи ой, а дробную часть — мантиссой. Пусть, например, lg x = 2,7536. Здесь 2 — хара теристи а, а 0,7536 — мантисса.
4°. Известно, что любое положительное число можно записать в стандартном виде: a · 10n, де 1 m a < 10; n Ý Z. По азатель n называют поряд ом данно о числа.
5°. Хара теристи а десятично о ло арифма числа a · 10n равна n, а мантисса равна lg a. Например:
lg 4650 = lg (4,65 · 103) = 3 + lg 4,65; lg 46,5 = lg(4,65 · 101) = 1 + lg 4,65;
lg 0,0465 = lg (4,65 · 10–2) = –2 + lg 4,65.
Та им образом, ло арифмы чисел, отличающихся дру от дру а толь о поряд ом, имеют одну и ту же мантиссу.
214

6°. Из у азанных выше свойств следует, что
lg 1 = 0, lg 10 = 1, lg 100 = 2, ..., lg 10n = n (n Ý Z); lg 0,1 = –1, lg 0,01 = –2, ..., lg 10–n = –n (n Ý Z).
6. Логарифмирование и потенцирование
1°. Ло арифмирование — это преобразование, при отором ло арифм выражения с переменными приводится сумме или разности ло арифмов переменных.
2°. Необходимо чет о различать сумму ло арифмов lg a + lg b и ло арифм суммы lg (a + b). Сумма ло арифмов равна ло а- рифму произведения, т. е. lg a + lg b = lg (ab), а для ло арифма суммы lg (a + b) формулы нет.
Пример. Дано: x = 3a2 5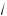 b3 , a > 0, b > 0, c > 0. Найти lg x.
b3 , a > 0, b > 0, c > 0. Найти lg x.
-----------------------
c4(a + b)
Р е ш е н и е. Ло арифмируя, получим
lg x = lg 3 + lg a2 + lg 5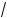 b3 – lg c4 – lg (a + b) =
b3 – lg c4 – lg (a + b) =
3 |
|
= lg 3 + 21g a + -- lg b – 4 lg c – lg (a + b). |
|
5 |
|
3°. Потенцирование — это преобразование, обратное ло а- |
|
рифмированию. |
|
3 |
|
Пример. Дано: lg x = 2 lg a – 5 lg b + -- lg c, a > 0, b > 0, c > 0. |
|
7 |
|
Требуется найти выражение для x. |
|
Р е ш е н и е. Потенцируя, получим |
|
lg x = lg a2 – lg b5 + lg c3/7 = |
|
a2c3 / 7 |
a2c3 / 7 |
= lg (a2c3/7) – lg b5 = lg ---------------- ; x = |
---------------- . |
b5 |
b5 |
7. Логарифмические уравнения
1°. Уравнение, содержащее переменную под зна ом ло а- рифма, называют ло арифмичес им. Простейшим примером ло арифмичес о о уравнения служит уравнение loga x = b ( де
a > 0, a − 1).
2°. Решение ло арифмичес о о уравнения вида loga f(x) = = loga g(x) основано на том, что та ое уравнение равносильно
уравнению f(x) = g(x) при дополнительных условиях f(x) > 0, g(x) > 0.
215

3°. Отметим, что переход от уравнения loga f(x) = loga g(x)
уравнению f(x) = g(x) может привести появлению посторонних орней. Та ие орни можно выявить либо с помощью подстанов и найденных значений в исходное ло арифмичес ое уравнение, либо с помощью нахождения области определения исходно о уравнения (эта область задается системой неравенств f(x) > 0, g(x) > 0).
Пример. Решить уравнение:
а) log3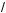 4 (x – 1) = 6; б) log3 (x2 – 4x – 5) = log3 (7 – 3x);
4 (x – 1) = 6; б) log3 (x2 – 4x – 5) = log3 (7 – 3x);
в) lg (x – 6) – 0,5 lg 2 = lg 3 + lg 
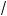 x – 10 .
x – 10 .
Р е ш е н и е. а) Со ласно определению ло арифма, имеем
x – 1 = (3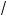 4 )6; x – 1 = (22/3)6; x – 1 = 24; x = 17.
4 )6; x – 1 = (22/3)6; x – 1 = 24; x = 17.
б) Данное уравнение сводится уравнению x2 – 4x – 5 = 7 – 3x, от уда получаем x2 – x – 12 = 0, т. е. x1 = 4, x2 = –3. Провер у вы-
полняем с помощью условий x2 – 4x – 5 > 0, 7 – 3x > 0. Значение x = 4 этой системе неравенств не удовлетворяет (и, следовательно, является посторонним орнем), а значение x = –3 удовлетворяет. Ита , x = –3 — единственный орень данно о уравнения.
в) Умножая обе части уравнения на 2 и используя свойства ло арифмов, имеем
2 lg (x – 6) – lg 2 = 2 lg 3 + lg (x – 10); lg (x – 6)2 = lg 2 + lg 32 + lg (x – 10); lg (x – 6)2 = lg 18(x – 10).
В результате данное уравнение сводится уравнению
(x – 6)2 = 18(x – 10), или x2 –30x + 216 = 0,
от уда x1 = 12, x2 = 18. Для провер и полученных значений
найдем область определения данно о уравнения; она задается системой неравенств x – 6 > 0, x – 10 > 0. Оба найденных значения этой системе удовлетворяют и, значит, служат орнями исходно о уравнения.
4°. При решении ло арифмичес их уравнений часто бывает полезен метод введения новой переменной.
Пример. Решить уравнение logx 5
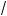 5 – 1,25 = logx2
5 – 1,25 = logx2
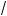 5 . Р е ш е н и е. Преобразуем данное уравнение:
5 . Р е ш е н и е. Преобразуем данное уравнение:
log |
|
5 |
3/2 |
5 |
= (log 5 |
1/2 |
) |
2 |
; |
3 |
|
5 |
= |
1 |
|
|
2 |
|
|
– -- |
|
|
-- log |
|
5 – -- |
-- log 5 |
|
. |
|||||||
|
x |
|
|
4 |
x |
|
|
|
|
2 |
x |
4 |
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
216

Пола ая logx 5 = y, получаем
3y |
5 |
y2 |
, или y2 |
– 6y + 5 = 0, |
------ |
– -- |
= ----- |
||
2 |
4 |
4 |
|
|
от уда y1 = 1, y2 = 5. Та им образом, приходим сово упности двух уравнений: logx 5 = 1; logx 5 = 5. Из перво о уравнения
находим x1 = 5, а из второ о получим x2 = 5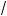 5 .
5 .
5°. При решении уравнений, содержащих переменную и в основании, и в по азателе степени, используют метод ло арифмирования. Если при этом в по азателе степени содержится ло арифм, то обе части уравнения надо проло арифмировать по основанию это о ло арифма.
Пример. Решить уравнение: |
|
|
|
|
а) x x = ( x )x; |
б) xlog2 x + 2 = 8. |
|
||
Р е ш е н и е. а) Ло арифмируем обе части уравнения по ос- |
||||
нованию x: |
|
|
|
|
x lg x = x lg x ; x lg x = |
1 |
1 |
x (2 – |
x )lg x = 0. |
-- x lg x; |
-- |
|||
|
2 |
2 |
|
|
Та а из условия следует, что x > 0, то последнее уравнение |
||||
равносильно сово упности уравнений 2 – |
|
x = 0; lg x = 0. Первое |
||
из них имеет орень x1 = 4, а второе — орень x2 = 1. Провер а
по азывает, что оба орня удовлетворяют данному уравнению. б) Проло арифмировав обе части уравнения по основанию 2,
получим
log2 (xlog2 x + 2 ) = log2 8; (log2 x + 2)log2 x = 3.
Теперь положим log2 x = y; то да уравнение примет вид y2 + 2y –
– 3 = 0, от уда y1 = 1, y2 = –3. Из уравнения log2 x = 1 находим
x1 = 2, а из уравнения log2 x = –3 находим x2 |
1 |
= -- . |
|
|
8 |
8. Логарифмические неравенства
1°. Неравенство, содержащее переменную под зна ом ло а- рифма, называют ло арифмичес им. Например, неравенства
вида
loga f(x) > loga ϕ(x); loga f(x) < loga ϕ(x),де a > 0, a − 1, являются ло арифмичес ими.
217
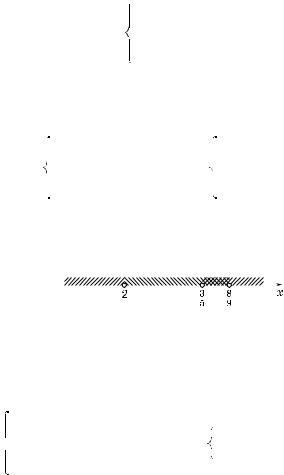
2°. Неравенство loga f(x) > loga ϕ(x) равносильно системе f(x) > > ϕ(x) > 0 при a Ý (1; +×) и системе 0 < f(x) < ϕ(x) при a Ý (0; 1).
3°. При решении ло арифмичес их неравенств следует учитывать общие свойства неравенств, свойство монотонности ло-арифмичес ой фун ции и область ее определения.
Примеры. 1. Решить неравенство log 5x – 3 > 1.
0,5 ----------------
x + 2
Р е ш е н и е. Выразив правую часть неравенства через ло-
арифм, получим log 5x – 3 > log 0,5. Это неравенство рав-
0,5 ---------------- 0,5 x + 2
носильно системе
 5x – 3 > 0,
5x – 3 > 0,
----------------
x + 2
 5x – 3 < 0,5,
5x – 3 < 0,5,
----------------
x + 2
первое неравенство оторой хара теризует область определения ло арифмичес ой фун ции, а второе — ее убывание при основании 0 < 0,5 < 1. Далее имеем
|
5x – 3 |
> 0, |
|
|
|
|
|
|
|
5x – 3 |
> 0, |
|||||||
|
|
|
|
|
||||||||||||||
|
-- |
-------------- |
|
|
|
|
|
|
|
---------------- |
||||||||
|
|
x + 2 |
|
|
|
|
|
|
_ |
|
|
x + 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5x – 3 – 0,5(x + 2) |
< 0 |
|
|
4,5x – 4 |
< 0. |
||||||||||||
|
|
|||||||||||||||||
|
|
|
x + 2 |
|
|
|
|
|
|
|
|
x + 2 |
|
|
|
|||
Решение последней системы иллюстрирует рис. 120. В ре- |
||||||||||||||||||
зультате получаем ответ: |
3 |
8 |
. |
|
|
|
|
|
|
|
|
|
|
|||||
-- ; |
9-- |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 120
2. Решить неравенство loga x + loga (x + 1) m loga (2x + 6),
aÝ (1; +×).
Ре ш е н и е. Имеем
x > 0, |
|
|
|
|
x + 1 > 0, |
_ |
|
x > 0, |
_ |
|
||||
|
||||
2x + 6 > 0, |
|
x(x + 1) m 2x + 6 |
||
|
|
|
||
loga x(x + 1) m loga (2x + 6) |
|
|
|
|
218

_ |
|
x > 0, |
_ |
|
x > 0, |
|
|
||||
|
|
||||
|
x2 – x – 6 m 0 |
|
(x – 3)(x + 2) m 0. |
||
|
|
|
|
Ответ: (0; 3].
3. Решить неравенство log2 (2x – 1) · log2 (2x + 1 – 2) < 2.
Р е ш е н и е. Та а 2x + 1 – 2 = 2(2x – 1), то данное неравенство можно записать в виде
log2 (2x – 1) · (log2 2 + log2 (2x – 1)) < 2 _ _ log2 (2x – 1) · (1 + log2 (2x – 1)) < 2.
Пола ая log2 (2x – 1) = y и учитывая, что x > 0, получим не-
равенство y(1 + y) < 2, или y2 + y – 2 < 0, от уда –2 < y < 1. Возвращаясь переменной x, получим
2–2 < 2x – 1 < 2; |
5 |
< 2x < 3; |
log |
|
5 |
< x < log |
|
3. |
-- |
2 |
-- |
2 |
|||||
|
4 |
|
|
4 |
|
|
Ита , интервал log |
|
5 |
; log |
|
3 |
— решение данно о неравенства. |
|
-- |
|
||||
|
2 |
4 |
|
2 |
|
|
9. Системы логарифмических уравнений и неравенств
Известные способы решения систем ал ебраичес их уравнений и неравенств применяются и решению систем, содержащих ло арифмичес ие уравнения и неравенства.
Примеры. 1. Решить систему уравнений
 xlg y = 100,
xlg y = 100, 
 logy x = 2.
logy x = 2.
Ре ш е н и е. Ло арифмируя первое уравнение при условиях x > 0, y > 0, x − 1, y − 1, получим lg y · lg x = 2. Из второ о урав-
нения следует, что y2 = x.
Решаем теперь полученную систему уравнений:
|
|
x = y2, |
|
|
_ |
|
x = y2, |
|
|
_ |
|
|
x = y2, |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
lg y · lg x = 2 |
|
lg y · lg y2 = 2 |
|
|
2 lg2 y = 2. |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
Последняя система распадается на две: |
|
|
|
|
|
|||||||||||
|
x = y2, |
_ |
|
x1 |
= 100, |
|
x = y2, |
_ |
|
x2 = 0,01, |
||||||
|
|
|
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|||||||||||||
|
lg y = 1 |
|
y1 |
= 10 |
и |
|
lg y = –1 |
|
y2 = 0,1. |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
Ответ: (100; 10); (0,01; 0,1).
219

2. Решить неравенство lg 7 – lg (– 8x – x2) > 0.
------------------------------------------------------
lg (x + 3)
Р е ш е н и е. Данное неравенство равносильно сово упности двух систем:
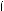 lg 7 – lg (–8x – x2) > 0,
lg 7 – lg (–8x – x2) > 0, 
 lg (x + 3) > 0;
lg (x + 3) > 0;
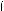 lg 7 – lg (–8x – x2) < 0,
lg 7 – lg (–8x – x2) < 0, 
 lg (x + 3) < 0.
lg (x + 3) < 0.
Решаем сначала систему (*):
|
7 |
|
|
|
|
|
7 |
|
|||
|
|
|
|
|
|||||||
|
lg ------------------------- > lg 1, |
|
|
|
------------------------- > 1, |
||||||
|
|
|
|
– 8x – x2 |
|
|
|
|
|
– 8x – x2 |
|
|
lg (x + 3) > lg 1, |
_ |
|
|
|
x + 3 > 1, |
_ |
||||
|
|
||||||||||
|
–8x – x2 > 0, |
|
|
|
|
|
8x + x2 < 0, |
||||
|
|
|
|
|
|
||||||
|
x + 3 > 0 |
|
|
|
|
|
x > –3 |
|
|||
|
|
|
7 |
|
|
|
7 + 8x + x2 |
< 0, |
|||
|
|
|
|
||||||||
|
|
|
-------------------- + 1 < 0, |
|
|
------------------------------- |
|||||
_ |
|
|
|
8x + x2 |
_ |
|
|
|
|
8x + x2 |
_ |
|
|
|
|
|
|
||||||
|
|
x > –2, |
|
|
x > –2, |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
8x + x2 < 0 |
|
|
|
8x + x2 < 0 |
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
7 + 8x + x2 > 0, |
|
|
|
(x + 7)(x + 1) > 0, |
|||
|
|
|
|
|
|
|
|||||
_ |
8x + x2 < 0, |
_ |
x(x + 8) < 0, |
||||||||
|
|
|
|
x > –2 |
|
|
|
|
|
x > –2. |
|
|
|
|
|
|
|
|
|
|
|
||
(*)
(**)
Множеством решений системы (*) служит промежуто (–1; 0) (рис. 121, а).
Решаем теперь систему (**):
lg |
7 |
< lg 1, |
–------8----x-----–-----x----2- |
 lg (x + 3) < lg 1, –8x – x2 > 0,
lg (x + 3) < lg 1, –8x – x2 > 0,
 x + 3 > 0
x + 3 > 0
 7 + 8x + x2 > 0,
7 + 8x + x2 > 0,
-------------------------------
8x + x2
_  x < –2,
x < –2,
8x + x2 < 0,  x > –3
x > –3
|
|
7 |
|
|
|
|
|
||
|
|
–------8----x-----–---x2 < 1,------- |
|
|
_ |
|
x + 3 |
< 1, |
_ |
|
||||
|
|
8x + x2 < 0, |
|
|
|
|
|
||
|
|
x + 3 |
> 0 |
|
 (x + 7)(x + 1) < 0, _
(x + 7)(x + 1) < 0, _  –3 < x < –2,
–3 < x < –2,
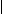 x(x + 8) < 0.
x(x + 8) < 0.
220
