
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf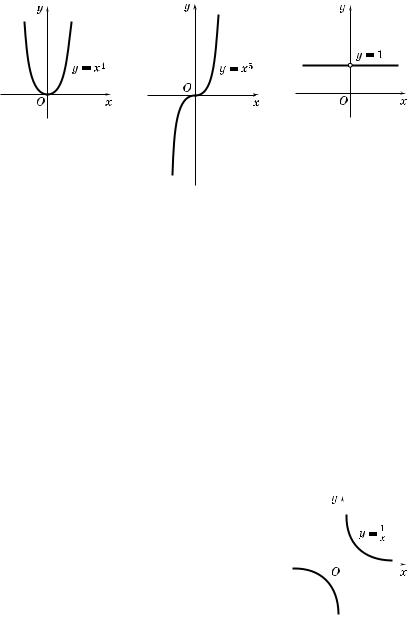
Рис. 94 |
Рис. 96 |
Рис. 95
2°. Отметим не оторые свойства степенной фун ции y = xk (k Ý N):
а) область определения — множество R всех действительных чисел;
б) при любом k рафи проходит через начало оординат и точ у (1; 1);
в) если k — четное число, то фун ция является четной и ось Oy служит осью симметрии рафи а;
) если k — нечетное число, то фун ция является нечетной и начало оординат служит центром симметрии рафи а.
3°. Рассмотрим фун цию y = x0, т. е. частный случай степенной фун ции при k = 0. Область определения этой фун ции — множество всех действительных чисел, роме нуля, т. е. D(f) =
= (–×; 0) (0; +×). Графи |
ом фун |
ции y = x0 служит прямая |
||||||||||
y = 1, из |
оторой удалена точ а (0; 1) |
|||||||||||
(рис. 96). |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||||||
|
4°. Рассмотрим теперь фун цию y = |
|
|
|
||||||||
= xk (k Ý Z–), т. е. степенную фун |
цию |
|
|
|
||||||||
|
|
|
|
|||||||||
с целым отрицательным по азателем. |
|
|
|
|||||||||
Если k = –1, то получается фун ция y = |
|
|
|
|
|
|||||||
|
|
|
|
|||||||||
= x |
–1 |
1 |
, рафи ом |
оторой служит |
|
|
|
|
||||
|
= -- |
|
|
|
||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
ипербола (рис. 97); если k = –2, то по- |
|
|
|
|||||||||
лучается фун ция y = x |
–2 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
= ----- , рафи |
|||||||||||
|
|
|
|
|
|
x2 |
|
Рис. 97 |
||||
|
|
|
|
|
|
|
161 |
|||||

|
|
|
|
оторой изображен на рис. 98. При нечет- |
|||
|
|
|
|
ном k рафи |
фун ции y = xk вы лядит |
||
|
|
|
|
та же, а |
и рафи |
фун ции y = x–1, |
|
|
|
|
|
а при четном k — |
а |
и рафи фун ции |
|
|
|
|
|
y = x–2. |
|
|
|
|
|
|
|
5°. Отметим не оторые свойства сте- |
|||
|
|
|
|
пенной фун |
ции y = xk (k Ý Z–): |
||
|
|
|
|
||||
|
|
|
|
а) область определения — множество |
|||
|
|
|
|
||||
Рис. 98 |
всех действительных чисел, роме нуля, |
||||||
|
|
|
|
т. е. D(f) = (–×; 0) (0; +×); |
|||
б) если k — четное число, то фун ция является четной и ось |
|||||||
Oy служит осью симметрии рафи а; |
|
|
|||||
в) если k — нечетное число, то фун |
ция является нечетной |
||||||
и ее рафи симметричен относительно начала оординат.
3. Функция y = k x
1°. Фун ция y = xk, k Ý N (k > 1) возрастает на множестве [0; +×), а множеством ее значений та же является множество [0; +×) (см. рис. 91—95). Значит, для фун ции y = xk существует обратная фун ция, определенная на множестве [0; +×) и принимающая значения из множества [0; +×). Эта обратная
фун ция обозначается та : y = k x .
2°. Для построения рафи а фун ции
Рис. 99 |
y = k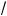 x , де x Ý [0; +×) и k Ý N (k > 1), можно воспользоваться свойством симметрии рафи ов взаимно обратных фун ций относительно прямой y = x (см. п. 1). На-
x , де x Ý [0; +×) и k Ý N (k > 1), можно воспользоваться свойством симметрии рафи ов взаимно обратных фун ций относительно прямой y = x (см. п. 1). На-
пример, рафи фун ции y = 3 x симмет-
x симмет-
ричен рафи у фун ции y = x3 относительно прямой y = x (рис. 99).
4. Иррациональные уравнения
1°. Уравнения, в оторых переменная содержится под знаом орня, называют иррациональными.
2°. Решение иррациональных уравнений сводится переходу от иррационально о рациональному уравнению с помощью возведения в степень обеих частей уравнения.
162

3°. При возведении обеих частей уравнения в четную степень возможно появление посторонних орней. Поэтому при использовании у азанно о метода следует проверить все найденные
орни подстанов ой в исходное уравнение. Пример. Решить уравнение:
а) 
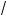 2x – 3 =
2x – 3 = 
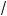 x – 2 ; б)
x – 2 ; б) 
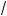 x – 1 = 3 – x.
x – 1 = 3 – x.
Р е ш е н и е. а) Возведя обе части уравнения в вадрат, получим 2x – 3 = x – 2, от уда x = 1. Провер а по азывает, что этот орень — посторонний (при x = 1 обе части уравнения не имеют смысла). Значит, данное уравнение не имеет орней.
б) Возведем обе части уравнения в вадрат:
x – 1 = (3 – x)2; x – 1 = 9 – 6x + x2; x2 – 7x + 10 = 0,
т. е. x = 2, x = 5. Провер ой убеждаемся, что x = 5 — посторонний орень, а x = 2 удовлетворяет уравнению.
4°. Заметим, про провер у можно упростить, если найти область определения данно о уравнения. Например, для уравнения
2x – 3 |
= x – 2 областью определения служит луч [2; +×) |
и та а |
1 Ô [2; +×), то x = 1 — посторонний орень. |
5. Иррациональные неравенства
Неравенства, в оторых переменная содержится под зна ом орня, называют иррациональными. Основным методом решения та их неравенств является метод возведения в степень. При этом решение иррациональных неравенств сводится решению рациональных неравенств или систем рациональных неравенств.
Пример. Решить неравенство:
а) 
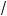 x – 1 < 3 – x; б)
x – 1 < 3 – x; б) 
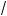 x – 1 > 3 – x.
x – 1 > 3 – x.
Р е ш е н и е. а) Область определения неравенства задается условием x – 1 l 0. Далее, по смыслу неравенства должно выполняться условие 3 – x > 0. При этих условиях обе части неравенства неотрицательны и поэтому можно использовать метод возведения в вадрат. В результате данное неравенство сводит-
ся следующей системе неравенств: |
|
||||
|
x – 1 l 0, |
|
|
x l 1, |
|
|
|
|
|||
|
3 – x > 0, |
_ |
|
x < 3, |
_ 1 m x < 2, |
|
|
||||
|
x – 1 < (3 – x)2 |
|
|
(x – 2)(x – 5) > 0 |
|
т. е. решением неравенства служит промежуто [1; 2).
163

б) Область определения неравенства та же задается условием x – 1 l 0. Если при этом 3 – x < 0, то выполняется и данное неравенство (та а в левой части о ажется неотрицательное число, а в правой — отрицательное). Если же 3 – x l 0, то, а и в предыдущем случае, обе части неравенства можно возвести
в вадрат. Та |
им образом, данное неравенство сводится сле- |
|||
дующей сово |
упности систем неравенств: |
|||
|
|
x – 1 l 0, |
|
x – 1 l 0, |
|
|
|
||
|
|
|
3 – x l 0, |
|
|
|
|
||
|
|
3 – x < 0; |
|
|
|
|
|
x – 1 > (3 – x)2. |
|
|
|
|
|
|
Решением первой системы служит от рытый луч (3; +×), а решением второй системы — промежуто (2; 3]. Объединяя эти множества, находим решение данно о неравенства: (2; +×).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Ка ую фун цию называют обратной по отношению данной?
2.Фун ция задана формулой
y = x2 на множестве {–2; –1; 0; 1; 2}. Найдите множество значений фун ции. Почему эта фун - ция не является обратимой?
3.Фун ция, заданная формулой y = 2x – 3, — возрастающая. Почему она обратима?
4.Фун ция, заданная форму-
лой y = x4 на множестве отрицательных чисел, — убывающая. Можно ли утверждать, что данная фун ция имеет обратную?
5.Относительно )рафи а а-ой фун ции симметричны )рафи и взаимно обратных фун - ций?
6.Задайте формулой фун - цию, обратную данной: а) y = 5x; б) y = –4x; в) y = 5x – 10; )) y =
=0,1x + 1.
7. До ажите, что фун ции,
заданные формулами y = 1 и
-------------
x – 2
y = 2x + 1 , взаимно обратны.
-----------------
x
8. Постройте )рафи фун - ции, заданной формулой y = xk при: а) k = 1; б) k = 2; в) k = 3; )) k = –1; д) k = –2; е) k = 1/2; ж) k = 1/3; з) k = –1/2.
9. До ажите, что а ово бы ни было натуральное число k, )рафи фун ции y = xk проходит через начало оординат и точ у (1; 1).
10. До ажите, что если k — четное число, то ось Oy служит осью симметрии )рафи а фун - ции y = xk.
11. До ажите, что если k — нечетное число, то начало оординат служит центром симметрии )рафи а фун ции y = xk.
164
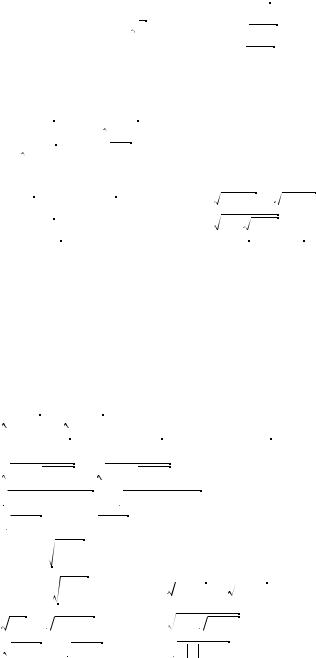
12. Даны две фун ции: y = xk,
)де x l 0 и k Ý N (k > 1), и y = k x . Постройте их в одной системе о- ординат. Ка ими общими свойствами они обладают?
x . Постройте их в одной системе о- ординат. Ка ими общими свойствами они обладают?
13. Найдите область определения фун ции:
а) y = 
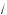 x – 5 ; б) y = 3
x – 5 ; б) y = 3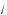 x – 1 ;
x – 1 ;
в) y = 4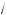 4 – x ; )) y =
4 – x ; )) y = 
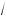 –x2 . 14. Постройте )рафи фун -
–x2 . 14. Постройте )рафи фун -
ции:
а) y = 
 x ; б) y =
x ; б) y = 
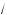 x – 1 ; в) y =
x – 1 ; в) y = 
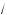 1 – x ;
1 – x ;
)) y = –
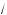 x – 1 ;
x – 1 ;
д) y = 
 x – 2 + 3; е) y = –
x – 2 + 3; е) y = –
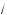 x – 2 + 3; ж) y =
x – 2 + 3; ж) y = 
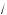 2 – x – 3.
2 – x – 3.
15.Ка ое уравнение называют иррациональным?
16.Почему при решении иррациональных уравнений необходимо делать провер у? Ка им образом ее можно упростить?
17.Объясните, почему не имеет решений уравнение:
а) |
x – 15 – 12 – x = 3; |
б) |
3 + x – 1 = 1; |
в) 
 x – 3 +
x – 3 + 
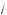 x + 3 = – 1.
x + 3 = – 1.
УПРАЖНЕНИЯ
1. Задайте формулой фун цию, обратную данной фун ции f. Постройте рафи и данной и обратной ей фун ций, если фун -
ция f задана формулой y = 5x + 4 , де x < 0.
-----------------
x
2. Решите уравнение:
а) 3 5 – x + 3
5 – x + 3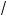 5 + x = 1;
5 + x = 1;
б) 
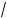 x2 + x + 4 +
x2 + x + 4 + 
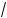 x2 + x + 1 =
x2 + x + 1 = 
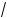 2x2 + 2x + 9 ; в) 3
2x2 + 2x + 9 ; в) 3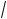 9 –
9 – 
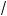 x + 1 + 3
x + 1 + 3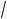 7 +
7 + 
 x + 1 = 4;
x + 1 = 4;
) 
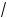 3x2 – 2x + 15 +
3x2 – 2x + 15 + 
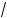 3x2 – 2x + 8 = 7; д) |
3x2 – 2x + 8 = 7; д) |
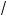 x – 5 – 2 | + |
x – 5 – 2 | + |
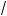 x – 5 – 3| = 1;
x – 5 – 3| = 1;
е) |
x------+-----1-- |
– |
-x-----–-----1-- |
= 1,5; |
|
|
x – 1 |
|
x + 1 |
|
|
ж) |
------x------- |
+ |
------x------- |
= 2; |
з) 3 x – 2 + x + 1 = 3; |
|
1 – x |
|
1 – x |
|
|
и) 3x – a – 3x = 1; |
) a – a + x = x; |
||||
л) 3 2 – x +
2 – x + 
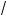 x – 1 = 1; м)
x – 1 = 1; м) 
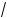 2 x – x2 = a.
2 x – x2 = a.
165
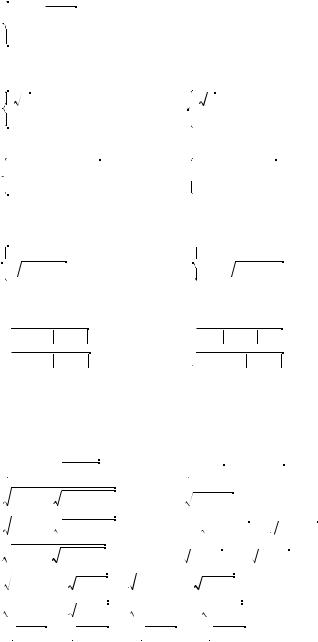
3. Решите систему:
а) 
 y =
y = 
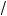 x – 3 ,
x – 3 ,
y + |x – 3| = 2.
Найдите частное x0 : y0; здесь и далее (x0; y0) — решение сис-
темы.
б) |
x = y, |
|x – 4| = y – 2. |
Найдите разность x0 – y0.
) 
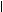 y + 2 =
y + 2 = 
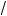 x + 4 ,
x + 4 ,  y + |x – 5| = 1.
y + |x – 5| = 1.
Найдите отношение x0 .
-----
y0
 |x – 3| = y + 4,
|x – 3| = y + 4,
е) 

 25 – x2 = y. Найдите сумму x0 + y0.
25 – x2 = y. Найдите сумму x0 + y0.
4. Решите уравнение:
а) 
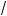 9 – 4x x – 4 = 4x + 3; в)
9 – 4x x – 4 = 4x + 3; в) 
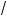 4 – 7x x + 2 = 3x + 2;
4 – 7x x + 2 = 3x + 2;
в) |
|
x – y = 0, |
|
||
|
y + |x – 4| = 2. |
|
|
Найдите произведение x0y0.
д) 
 y +
y + 
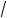 16 – x2 = 0,
16 – x2 = 0,  y + 1 = |x – 5|.
y + 1 = |x – 5|.
Найдите разность y0 – x0.
 y(x – 2) = 6,
y(x – 2) = 6,
ж) 
y +  (x – 3)2 = 0. Найдите разность x0 – y0.
(x – 3)2 = 0. Найдите разность x0 – y0.
б) 
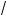 25x x – 1 + 4 = 5x – 3;)
25x x – 1 + 4 = 5x – 3;) 
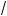 36 + 5x x + 3 = 6 + x.
36 + 5x x + 3 = 6 + x.
З а м е ч а н и е. В этом и следующем упражнениях приведены нетрадиционные иррациональные уравнения, оторые были предложены на ЕГЭ.
5. Решите уравнение:
а) 
 2x + 2
2x + 2
 x2 – 9 + 2x = 9 + 2
x2 – 9 + 2x = 9 + 2
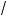 x + 3 +
x + 3 + 
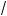 x – 3 ;
x – 3 ;
б) 4x + 2 |
4x2 – 25 + 4 = x + 2x + 5 ; |
||
в) 6x + 2 |
9x2 – 49 + 11 = x + 2 3x + 7 + 3x – 7 ; |
||
) |
2x – 2 x2 – 16 + x = 16 + x + 4 – 2 x – 4 ; |
||
д) x + 3 – 4 |
x – 1 + x + 3 + 2 x + 2 = 4; |
||
е) |
x + 5 + 2 |
x + 4 + x + 13 – 6 x + 4 = 4; |
|
ж) 
 x – 1 +
x – 1 + 
 x + 7 = 2
x + 7 = 2
 x – 2 + 2
x – 2 + 2
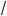 x + 2 ;
x + 2 ;
166






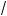 11x + 3 +
11x + 3 + 
 x – 2 =
x – 2 = 
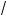 9x + 7 +
9x + 7 + 
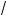 2 – x ; и) 2(
2 – x ; и) 2(
 x + 36 –
x + 36 – 
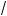 x + 1 ) = 5(
x + 1 ) = 5(
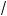 x + 4 –
x + 4 – 
 x ); )
x ); ) 
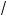 x – 3 –
x – 3 – 
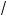 4x – 19 =
4x – 19 = 
 18 – 2x –
18 – 2x – 
 x + 2 ;
x + 2 ;
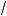 x + 11 +
x + 11 + 
 x + 2 ) = 3(
x + 2 ) = 3(
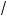 x + 18 +
x + 18 + 
 x + 3 ).
x + 3 ).
 3 = 0 и x
3 = 0 и x 52 ; x
52 ; x 52 .
52 . x – 5 – 2 = 0,
x – 5 – 2 = 0,  x – 5 – 3 = 0, т. е. x
x – 5 – 3 = 0, т. е. x x – 5 – 2 и
x – 5 – 2 и 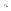 x – 5 – 3 в этих промежут ах (рис. 101).
x – 5 – 3 в этих промежут ах (рис. 101).
 x – 5 + 2 –
x – 5 + 2 – 
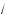 x – 5 + 3 = 1;
x – 5 + 3 = 1; 
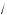 x – 5 = 2, x = 9; б) если x Ý (9; 14], то
x – 5 = 2, x = 9; б) если x Ý (9; 14], то 
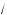 x – 5 – 2 –
x – 5 – 2 – 
 x – 5 + 3 = 1; 1 = 1; x Ý (9; 14];
x – 5 + 3 = 1; 1 = 1; x Ý (9; 14];
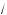 x – 5 – 2 +
x – 5 – 2 + 
 x – 5 – 3 = 1;
x – 5 – 3 = 1; 
 x – 5 = 3, x = 14 Ô (14; +×).
x – 5 = 3, x = 14 Ô (14; +×).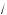 x – 2 = u,
x – 2 = u, 
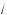 x + 1 = v, то)да данное уравнение будет э вивалентно системе
x + 1 = v, то)да данное уравнение будет э вивалентно системе
 3x –
3x – 
 a – 3x > 0, та а правая часть уравнения (1) — положительное число.
a – 3x > 0, та а правая часть уравнения (1) — положительное число.