
4.Решив последнее уравнение, находим y1 = –1 (не подходит); y2 = 9,
т.е. 3x = 9. Ита , x = 2.
К упражнению 14
1. Имеем b2 = b1q, b4 = b1q3, b6 = b1q5. То$да, со$ласно условию, получаем систему уравнений
|
|
|
|
|
|
|
|
|
|
|
|
b1q |
3 |
– b1q |
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= –------ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1q |
5 |
– b1q |
3 |
= – |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
--------- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
512 |
|
|
2. Перепишем эту систему та : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1q(q |
2 |
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– 1) = –------ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
(q |
2 |
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1q |
|
|
– 1) = –--------- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
512 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
3. Разделив почленно второе уравнение на первое, получим q |
= ------ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
Следовательно, q1 |
= |
1 |
1 |
|
|
|
|
|
|
|
|
-- |
, q2 = – -- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
4. Подставим поочередно эти значения q в первое уравнение системы: |
|
|
1 1 |
– 1 |
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
а) b1 · -- |
------ |
|
= –------ , от уда b1 = 6; |
|
|
|
|
4 |
16 |
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
б) b1 |
|
1 |
1 |
– 1 |
|
45 |
|
|
|
|
|
|
|
|
|
|
|
–-- |
------ |
|
= – ------ , от уда b1 = –6. |
|
|
|
4 |
16 |
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
5. Ита , получаем два решения: а) b1 |
1 |
; б) b1 = –6, q |
1 |
= 6, q = -- |
= – -- . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
К упражнению 15
1. Та а b2 = b1q, b5 = b1q4, b6 = b1q5, то, используя условие, получаем систему
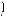 b1(1 + q4) = 51,
b1(1 + q4) = 51,  b1q(1 + q4) = 102.
b1q(1 + q4) = 102.
2.Решив эту систему, находим q = 2, b1 = 3.
3.Теперь воспользуемся формулой суммы членов $еометричес ой про$рессии:
S = b1(qn – 1) . n --------------------------
q – 1
Подставив в эту формулу значения q = 2 и b1 = 3, получим
3069 = 3(2n – 1) , или 1024 = 2n, или 210 = 2n,
------------------------
2 – 1
от уда n = 10.
К упражнению 16
1. Перепишем условие та :
а) òò b1, b2, b3; б) ò b1, b2 + 2, b3; в) òò b1, b2 + 2, b3 + 9.
2. Используя хара теристичес ие свойства арифметичес ой и $еометричес ой про$рессий, запишем систему
 2(b2 + 2) = b1 + b3,
2(b2 + 2) = b1 + b3,
 (b2 + 2)2 = b1(b3 + 9).
(b2 + 2)2 = b1(b3 + 9).
3. Выразим теперь b2 и b3 через b1 и q и получим систему двух уравнений с двумя неизвестными:
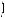 2(b1q + 2) = b1 + b1q2,
2(b1q + 2) = b1 + b1q2, 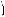 (b1q + 2)2 = b1(b1q2 + 9).
(b1q + 2)2 = b1(b1q2 + 9).
4. Решив эту систему, найдем b1 = 4, q = 2 или b1 |
4 |
, q = –4. |
= ------ |
|
|
|
|
25 |
|
Ответ: 4, 8, 16 или |
4 |
16 |
64 |
|
|
------ |
, –------ |
, ------ . |
|
|
|
25 |
25 |
25 |
|
|
К упражнению 18
1. Пусть b — первый член ис омой про$рессии, а q — ее знаменатель. По условию числа b, bq, bq2 – 4 образуют арифметичес ую про- $рессию с разностью 2; следовательно,
bq – b = bq2 – 4 – bq = 2. |
(1) |
2. Из равенств (1) составим систему с двумя неизвестными b и q:
|
b(q – 1) = 2, |
(2) |
|
bq(q – 1) = 6. |
|
|
3.Решив систему (2), найдем q = 3, b = 1.
4.Ита , ис омая про$рессия имеет вид 1, 3, 9, ... .
К упражнению 22
1. Пусть S — сумма всех членов $еометричес ой про$рессии, а S1 — сумма членов этой про$рессии, находящихся на нечетных местах.
252

2.Члены $еометричес ой про$рессии, находящиеся на нечетных местах, образуют $еометричес ую про$рессию со знаменателем q2, $де q — знаменатель данной про$рессии.
3.По условию S = 3S1, т. е.
|
|
b1(q2n – 1) |
b1 (q2n – 1) |
|
|
|
|
|
|
----------------------------- = 3 |
----------------------------- . |
|
|
|
|
|
|
q |
– 1 |
q2 |
– 1 |
|
|
|
|
4. |
Решив это уравнение, находим q = 2. |
|
|
|
|
К упражнению 23 |
|
|
|
|
|
|
|
|
1. |
Представим данную дробь в следующем виде: |
|
|
|
|
7 |
7 |
+ |
7 |
7 |
1 + |
1 |
1 |
+ ... . |
|
0,(7) = ------ |
+ --------- |
------------- + ... = ------ |
------ + |
--------- |
|
10 |
100 |
|
1000 |
10 |
|
10 |
102 |
|
|
2. |
Выражение в с об ах представляет собой сумму бес онечно |
|
|
|
|
|
|
|
|
|
1 |
|
убывающей $еометричес ой про$рессии со знаменателем ------ . |
|
|
|
|
|
|
|
|
|
|
10 |
|
3. |
Эту сумму найдем по формуле |
|
b1 |
|
|
1 |
10 |
S = ------------ , т. е. S = |
-------- = |
------ . |
|
|
|
|
|
1 – q |
|
|
0,9 |
9 |
4. |
|
7 |
10 |
7 |
|
|
|
|
|
|
Ита , 0,(7) = ------ · |
------ |
= -- . |
|
|
|
|
|
|
|
|
10 |
9 |
9 |
|
|
|
|
|
|
К упражнению 25
1. Пусть ABCD — данный вадрат, A1B1C1D1 — вписанный в ABCDвадрат, A2B2C2D2 — вписанный в A1B1C1D1 вадрат и т. д. (рис. 132).
2. Положим B1C1 = x и B2C2 =
= y; то$да P1 = PA1B1C1D1 |
= 4x, а P2 = |
= PA2B2C2D2 |
= 4y. |
|
3. В равнобедренном прямоу$оль- |
ном треу$ольни е B1CC1 имеем B1C1 = |
= 2 B1C = |
2 |
k |
------ BC, т. е x |
= ------ . То$да |
|
2 |
2 |
|
|
P1 = 4x = 2 |
2 k. |
|
4. В равнобедренном прямоу$ольном треу$ольни е B2B1C2 имеем
B2C2 = 2 B1C2 = |
2 |
B1C1 |
= |
------ |
|
|
2 |
|
|
k |
. То$да P2 |
= 4y = 2k. |
т. е. y = -- |
2 |
|
|
|
|

5. Ита , нам известны периметры трех вадратов: PABCD = P = 4k,
PA1B1C1D1 = P1 = 2
 2 k, PA2B2C2D2 = P2 = 2k.
2 k, PA2B2C2D2 = P2 = 2k.
6. Ле$ о установить, что числа P, P1 и P2 являются тремя последовательными членами $еометричес ой про$рессии. Действительно, для
этих чисел выполняется ее хара теристичес ое свойство: P21 = PP2,
та а (2
 2 k)2 = 4k · 2k, или 8k2 = 8k2. 7. Найдем знаменатель про$рессии:
2 k)2 = 4k · 2k, или 8k2 = 8k2. 7. Найдем знаменатель про$рессии:
|
q = |
P1 |
= |
P2 |
= |
1 |
, т. е. 0 < q < 1. |
|
--P---- |
P-----1- |
--2- |
|
|
|
|
|
8. Чтобы найти сумму периметров всех вписанных вадратов, вос-
пользуемся формулой S = |
-----P------ |
- . То$да получим |
|
|
|
1 – q |
S = ------ |
4----k------- |
= --4-------- |
2----k--- |
= 4 2 ( 2 + 1)k = 4(2 + 2 )k. |
|
1 |
|
|
|
9. Рассуждая анало$ично, найдем сумму площадей всех вписанных вадратов. Пусть F — площадь вадрата ABCD, т. е. F = k2; да-
лее, F1 = x |
2 |
k2 |
= y |
2 |
k2 |
|
= ----- — площадь вадрата A1B1C1D1; F2 |
|
= ----- — пло- |
|
|
2 |
|
|
4 |
щадь вадрата A2B2C2D2 и т. д. Последовательность этих площадей
образует $еометричес ую про$рессию со знаменателем q = 1 . Та им
--
2
образом, сумма площадей всех вписанных вадратов составит
F |
k2 |
|
2 |
S = ------------ |
= ------------- |
= 2k . |
1 – q |
1 – |
1 |
|
|
-- |
|
|
|
2 |
|
К упражнению 27
1. Пусть v ( м/ч) — первоначальная с орость мотоци листа.
2. То$да на поезд у от A до B (рис. 133) он затратил 120 (ч).
---------
v
Рис. 133

3. Путь от B до C (пун та, $де он остановился) мотоци лист в течение 1 ч ехал со с оростью v ( м/ч), т. е. расстояние между B и C равно v · 1 = v ( м).
4. Следовательно, расстояние между C и A равно 120 – v ( м).
5. Это расстояние мотоци лист проехал со с оростью v + 6 ( м/ч).
6. |
Значит, на поезд у от C до A он затратил 120------------–------v- |
(ч). |
|
|
|
v + 6 |
|
7. |
Та а на поезд у от A до B мотоци лист затратил столь о же |
времени, что и на поезд у от B до A, то получаем уравнение |
|
120--------- |
= 1 + 1-- |
+ 120------------–------v- . |
|
|
v |
6 |
v + 6 |
|
8. Решив е$о, находим v = 48 ( м/ч).
К упражнению 29
З а м е ч а н и е. Напомним не оторые теоретичес ие сведения, позволяющие, не решая систему линейных уравнений, определить о- личество ее решений по известным оэффициентам при неизвестных и свободным членам.
Пусть дана система
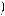 a1x + b1y = c1,
a1x + b1y = c1,  a2x + b2y = c2,
a2x + b2y = c2,
$де a1, a2, b1 и b2 — оэффициенты при неизвестных, а c1 и c2 — свободные члены. Возможны три случая.
1. Если |
a1 |
|
b1 |
, т. е. оэффициенты при неизвестных не пропор- |
----- |
− ----- |
|
a2 |
|
b2 |
|
циональны, то система имеет единственное решение. |
2. Если |
a1 |
= |
b1 |
c1 |
----- |
----- |
− ---- , т. е. оэффициенты при неизвестных про- |
|
a2 |
|
b2 |
c2 |
порциональны между собой, но не пропорциональны свободным членам, то система не имеет решений.
a1 |
b1 |
c1 |
, т. е. оэффициенты при неизвестных и сво- |
3. Если ----- |
= ----- |
= ---- |
a2 |
b2 |
c2 |
|
бодные члены пропорциональны между собой, то система имеет бес о- нечное множество решений.
Решение пражнения 29а. I способ. Система имеет единственное
k |
1 |
, т. е. если k − –1. |
решение, если -- |
− ------ |
1 |
–1 |
|
II способ. 1. Сложив оба уравнения системы, получим x(k + 1) = 5.

2. |
Если k − –1, то система имеет единственное решение x = |
------5------- |
, |
|
|
|
|
k + 1 |
|
y = x – 3 = |
------5------- |
– 3 = 2-----–------3----k- . |
|
|
|
|
k + 1 |
k + 1 |
|
|
3. |
Если k = –1, то получим систему |
|
|
 –x + y = 2,
–x + y = 2,  x – y = 3,
x – y = 3,
оторая не имеет решений.
Решение пражнения 29б. I способ. 1. Система не имеет решений, если
|
|
|
------3------- |
= |
k-----–-------1 − k-----+------1-- . |
(1) |
|
|
|
k + 1 |
|
1 |
|
3 |
|
2. |
Из равенства |
------3------- |
= ------k –-----1- |
следует, что k1 = 2, k2 = –2. |
|
|
|
k + 1 |
|
1 |
|
|
|
|
|
3. |
Подставив значение k1 = 2 в (1), получим |
|
|
|
|
|
3 |
= |
1 |
= |
3 |
|
|
|
|
|
-- |
1-- |
3-- |
|
|
|
|
|
3 |
|
|
|
(в этом случае система имеет бес онечное множество решений, см. замечание).
4. Подставив значение k2 = –2 в (1), получим
3 = –3 –1 ,
------ ------ − ------
–1 1 3
т.е. при k = –2 система не имеет решений.
II способ. 1. Из второ$о уравнения системы выразим y = 3 – (k + 1)x и подставим это выражение в первое уравнение:
3x + (k – 1)(3 – (k + 1)x) = k + 1, или x(k – 2)(k + 2) = 2(k – 2).
2. Последнее уравнение, а, значит, и данная система не имеют решений при k = –2.
Решение пражнения 29в. 1. Система имеет бес онечное множество решений, если
|
2----k-- |
= |
--1---- |
= 6----k----2----–-----5----k-----+------1-- . |
|
(1) |
|
1 |
|
2k |
0 |
|
|
|
2. Из равенства 2----k-- |
= -- |
1---- |
следует, что k1 |
= –1-- |
, k2 |
= 1-- . |
1 |
2k |
|
|
2 |
|
2 |
3. Равенство --1---- = |
6----k----2-----–----5-----k----+--------1 следует понимать та , что числитель |
2k |
|
0 |
|
|
|
|
|
второй дроби та же равен нулю, т. е. |
|
|
|
|
|
6k2 – 5k + 1 = 0. |
|
|
(2) |
4. Из уравнения (2) находим k1 |
1 |
, k2 |
1 |
. Ита , система имеет |
= -- |
= -- |
|
2 |
|
3 |
|
бес онечное множество решений при k = 1 .
--
2
К упражнению 31а
1. Сначала определим множество значений x, для оторых данное неравенство существует:
 x2 – x l 0,
x2 – x l 0,
2 – x2 – x l 0, 
 x l 0,
x l 0,

 x – 1 l 0,
x – 1 l 0,
или
 x(x – 1) l 0,
x(x – 1) l 0,
 (x + 2)(x – 1) m 0,
(x + 2)(x – 1) m 0,
Рис. 134
x l 1.
2. Решив эту систему неравенств (рис. 134), за лючаем, что ОДЗ неравенства состоит толь о из двух чисел: x1 = 0 и x2 = 1.
3. Провер а по азывает, что решением данно$о неравенства является лишь одно число, а именно x = 1.
Т е м а 14
À
Поворот точки вокруг начала координат. Градусное и радианное измерение угловых величин. Тригонометрические функции числового аргумента. Знаки тригонометрических функций.
Зависимость между тригонометрическими функциями одного и того же аргумента.
Вычисление значений тригонометрических функций некоторых углов.
Четность и нечетность тригонометрических функций. Периодичность тригонометрических функций.
Свойства тригонометрических функций. Формулы сложения. Формулы приведения
Теоретичес ие сведения
1. Поворот точки вокруг начала координат
1°. В теме 3 было отмечено, что между множеством действительных чисел R и множеством точе числовой прямой можно установить соответствие, при отором аждой точ е числовой прямой соответствует единственное действительное число и, наоборот, аждому действительному числу соответствует единственная точ а числовой прямой.
2°. Между действительными числами и точ ами о ружности та же можно установить соответствие, что позволяет опреде-
лить три онометричес ие фун ции чис- |
|
лово о ар умента. |
|
3°. О ружность единично о радиу- |
|
са с выбранными началом отсчета и на- |
|
правлением обхода называют числовой |
|
о р жностью. |
|
4°. Каждой точ е M о ружности со- |
|
ответствует бес онечное множество |
|
ду , начинающихся в точ е A (рис. 135) |
|
и за анчивающихся в точ е M. Одной |
Рис. 135 |

из них является ратчайшая ду а, соединяющая эти две точ-и, а все остальные получаются из ратчайшей ду и прибавлением или вычитанием цело о числа полных оборотов.
5°. а) Если точ а, дви аясь по числовой о ружности от точ-и A против часовой стрел и, прошла путь длиной α (рис. 136), то принято считать, что α > 0. Конечную точ у пути обозначим через P.
В этом случае оворят, что точ а P получена из точ и A поворотом (обходом) во ру начала оординат на у ол α.
Отметим, что если 0 < α m π, то у ол AOP равен α а центральный у ол числовой о ружности.
б) Если точ а, дви аясь по числовой о ружности от точ и A по часовой стрел е, прошла путь длиной α (рис. 137), то принято считать, что α < 0.
в) Поворот на 0° означает, что точ а A остается на месте.
2. Градусное и радианное измерение угловых величин
1°. Из урса еометрии известно, что у лы можно измерять в радусах. Например, развернутый у ол равен 180°, прямой у ол равен 90°.
2°. За единицу измерения у лов и ду принимают у ол в один рад с (обозначение: 1°).
3°. У ол в 1° — это у ол, оторый опишет начальный радиус,
совершив 1 часть полно о оборота во ру своей начальной
---------
360
точ и против часовой стрел и.
4°. Мин той (обозначение: 1′) называют 1 часть радуса.
------
60
Рис. 138
5°. Се ндой (обозначение: 1′′) называют 1 часть минуты.
------
60
6°. Кроме радусной меры существуют и дру ие единицы измерения у лов. В математи е и физи е обычно используют радианную меру у ла.
7°. Центральный у ол, опирающийся на ду у, длина оторой равна радиусу, называют у лом в один радиан (рад).
8 |
° |
. У ол в один радиан содержит |
180 |
радусов: |
|
--------- |
|
|
|
|
|
π |
|
|
|
1 рад = |
180 |
|
° |
(1) |
|
|
--------- |
. |
|
|
|
π |
|
|
|
9°. Один радиан приближенно равен 57° 18′.
10°. Из равенства (1) следует, что у ол в α радианов содер-
180 |
|
|
|
|
|
|
жит --------- α радусов, т. е. |
|
|
|
|
|
|
π |
|
|
|
|
|
|
α рад = |
180 |
|
° |
|
|
|
|
|
(2) |
--------- α . |
|
|
|
π |
|
|
|
|
11°. Из равенства 180° = π выте ает, что: |
|
|
π |
|
|
π |
20°π |
π |
а) 360° = 2π; б) 90° = -- |
; в) 30° = -- |
; ) 20° = ------------ |
= -- . |
2 |
|
|
6 |
180 |
° |
9 |
3. Тригонометрические функции числового аргумента
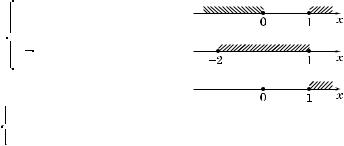
1°. Пусть задано не оторое число x; отметим соответствующую ему точ у K(x) числовой о ружности.
2°. Ординату точ и K(x) называют син сом числа x и обозначают sin x, а абсциссу этой точ и называют осин -
сом числа x и обозначают cos x.
3°. Дру ими словами, sin x равен ве-
личине (т. е. длине, взятой с соответствующим зна ом) отрез а KE, а cos x — величине отрез а OE (рис. 138).
4°. При вращении радиуса о ружности он будет «пробе ать» через точ у K(x) бес онечное множество раз ( а по ча-



 2(b2 + 2) = b1 + b3,
2(b2 + 2) = b1 + b3, (b2 + 2)2 = b1(b3 + 9).
(b2 + 2)2 = b1(b3 + 9).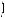 2(b1q + 2) = b1 + b1q2,
2(b1q + 2) = b1 + b1q2, 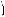 (b1q + 2)2 = b1(b1q2 + 9).
(b1q + 2)2 = b1(b1q2 + 9).






 b
b b
b
 2 k, P
2 k, P
 2 k)
2 k) a
a a
a –x + y = 2,
–x + y = 2,  x – y = 3,
x – y = 3, x
x
 x l 0,
x l 0,
 x – 1 l 0,
x – 1 l 0, x(x – 1) l 0,
x(x – 1) l 0, (x + 2)(x – 1) m 0,
(x + 2)(x – 1) m 0,