
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf3. Та им образом, на долю заряда остается 1 массы патрона.
------
12
4. Обозначив массу патрона через x, получаем пропорцию
1
------
-------- -- --------
12 = 1 , от уда x = 0,8 = 9,6 ( )).
0,8 x 1
------
12
К упражнению 29
1.Процент прибыли берется по отношению себестоимости (принимаемой за 100%).
2.Следовательно, продажная цена 1386 р. составляет 100% + 10% =
=110% от себестоимости.
3.Обозначив себестоимость через x, получаем пропорцию
--1386-------------- |
= |
-------x--------- |
, т. е. x = 1260 (р.). |
110% |
|
100% |
|
К упражнению 30
1.Убыто исчисляется в процентах по отношению себестоимости (принимаемой за 100%).
2.Значит, 3348 р. — это 96% себестоимости.
3.Пусть x — себестоимость проду ции. То)да получим пропорцию
-------x--------- |
= 3348------------- |
, от уда x = 3487,5 (р.). |
100% |
96% |
|
121
Т е м а 8
À
Неравенства. Основные свойства неравенств. Действия с неравенствами. Доказательство неравенств. Неравенства, содержащие переменную.
Решение линейных и квадратных неравенств
Теоретичес ие сведения
1. Неравенства
1°. При сравнении двух действительных чисел x и y возможны три случая: x = y (x равно y); x > y (x больше y) и x < y (x меньше y). При этом:
x = y то'да и толь о то'да, о'да разность x – y равна нулю; x > y то'да и толь о то'да, о'да разность x – y положи-
тельна (например, 6 > 2, та а 6 – 2 = 4 > 0);
x < y то'да и толь о то'да, о'да разность x – y отрицательна (например, 6 < 10, та а 6 – 10 = –4 < 0).
2°. Используя зна равносильности, утверждения п. 1° можно записать в следующем виде:
x = y _ x – y = 0; x > y _ x – y > 0; x < y _ x – y < 0.
3°. Часто употребляется запись x l y или, что то же самое, y m x. Это означает, что либо x > y, либо x = y и читается та : «x не меньше y» или «x больше или равно y».
4°. Символичес ую запись, в оторой два числа или два выражения, содержащие переменные, соединены зна ом >, <, l или m, называют неравенством.
5°. Неравенства, составленные с помощью зна ов l или m, называют нестро ими; неравенства, составленные с помощью зна ов > или <, — стро ими.
6°. Два неравенства вида a > b и c > d называют неравенствами одина ово о смысла. Например, 5 > 2 и –3 > –6 — это неравенства одина ово'о смысла, а неравенства 5 > 3 и 6 < 10 являются неравенствами противоположно'о смысла.
122
7°. Кроме неравенств вида x > y, x < y, употребляются еще неравенства вида x < a < y, оторые называют двойными неравенствами.
8°. Выс азывание x < a < y истинно то'да и толь о то'да,о'да одновременно истинны оба выс азывания: a > x и a < y, т. е. (x < a < y) _ (x < a) ∩ (a < y).
9°. Двойное неравенство x m a < y означает, что (x m a < y) _ _ ((x < a) (x = a)) ∩ (a < y).
10°. Неравенства, содержащие толь о числа, называют числовыми. Например, 5 > 3; –3 < 0; –2 > –5 — числовые неравенства.
11°. Если неравенство представляет собой истинное выс а- зывание, то е'о называют верным.
12°. Если неравенство содержит бу венные выражения, то оно является верным лишь при определенных значениях входящих в не'о переменных. Например, неравенство (a + b)2 l 0 верно при любых значениях a и b, та а вадрат любо'о числа есть число неотрицательное; неравенство x2 > 0 верно при любых значениях x, роме нуля.
2. Основные свойства неравенств
1°. Если a > b, то b < a.
2°. Если a > b и b > c, то a > c (свойство транзитивности). 3°. Если обеим частям верно о неравенства прибавить одно и то же число, то получится верное неравенство, т. е. ес-
ли a > b, то a + c > b + c.
4°. Если из одной части верно о неравенства перенести в дру ую а ое-либо сла аемое, изменив е о зна на противоположный, то получится верное неравенство, т. е. если a + b > c, то a – c > –b.
5°. Если обе части верно о неравенства умножить на одно и то же положительное число, то получится верное неравенство. Например, если a > b, то 5a > 5b.
6°. Если обе части верно о неравенства умножить на одно и то же отрицательное число и изменить зна неравенства на противоположный, то получится верное неравенство. Например, если a > b, то a · (–1) < b · (–1), т. е. –a < –b.
7°. Та а деление можно заменить умножением на число, обратное делителю, то анало'ичные правила справедливы и для
деления. Например, если a > b, то 1 a >
--
3
1 b и –1 a < –1 b.
-- -- --
3 5 5
123
3. Действия с неравенствами
1°. Неравенства одина ово'о смысла можно почленно с ладывать. Например,
+ |
a > b |
|
+ |
a < m |
|
|||
c > d |
или |
b < n |
|
. |
||||
|
|
|
|
|
||||
a + c > b + d |
|
a + b < m + n |
|
|||||
2°. Неравенства противоположно'о смысла можно почленно вычитать, оставляя зна то'о неравенства, из оторо'о производится вычитание. Например,
– |
a > b |
||
c < d |
. |
||
|
|||
a – c > b – d
3°. Неравенства одина ово'о смысла с положительными членами можно почленно умножать. Например, если a > b > 0 и c > d > 0, то ac > bd.
4°. Обе части неравенства с положительными членами можно возводить в одну и ту же натуральную степень. Например, если a > b, то ak > bk, 'де a > 0, b > 0, k Ý N.
Верно и обратное утверждение: если ak > bk, a > 0, b > 0, k Ý N, то a > b.
4. Доказательство неравенств
У ажем не оторые приемы до азательства неравенств.
1°. Использование определения понятия «больше» или «меньше» (т. е. рассмотрение разности между левой и правой частями неравенства).
Пример. До азать, что |
a-----+------b- |
l |
ab , если a l 0, b l 0. |
|
2 |
|
|
Р е ш е н и е. Рассмотрим разность
a-----+------b- |
– |
ab = a------+-----b-----–-----2--------ab----- |
= |
|
2 |
|
|
2 |
|
|
|
a + b |
l ab . |
|
Следовательно, ------------ |
|
|||
|
|
2 |
|
|
(-------a-----–----------b---)--2- |
l 0. |
2 |
|
Это неравенство означает, что среднее арифметичес ое двух
неотрицательных чисел не меньше их средне о еометричес о-о, причем равенство дости ается толь о в том случае, о - да a = b.
124

2°. Использование известных неравенств.
a |
b |
l 2, если a > 0, b > 0. |
|
Пример. До азать, что -- |
+ -- |
||
b |
a |
|
|
|
a |
b |
положительны, то их сред- |
Р е ш е н и е. Та а числа -- |
и -- |
||
|
b |
a |
|
нее арифметичес ое не меньше средне'о 'еометричес о'о, т. е.
a |
b |
l 2 |
a |
b |
, или |
a |
b |
l 2. |
-- |
+ -- |
-- |
-- |
-- |
+ -- |
|||
b |
a |
|
b |
a |
|
b |
a |
|
Ита , сумма двух взаимно обратных положительных чисел не меньше 2.
3°. Использование действий с неравенствами (почленное сложение, вычитание, умножение и др.).
Примеры. 1. До азать, что
a + b + c l 
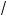 ab +
ab + 
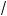 bc +
bc + 
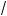 ac , если a l 0, b l 0, c l 0.
ac , если a l 0, b l 0, c l 0.
Р е ш е н и е. Для неотрицательных чисел a, b и c верны неравенства
a + b |
l ab ; |
b + c |
l bc ; |
a + c |
l ac . |
------------ |
------------ |
------------ |
|||
2 |
|
2 |
|
2 |
|
С ладывая эти неравенства почленно, после упрощения получим
a + b + c l 
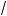 ab +
ab + 
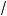 bc +
bc + 
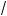 ac .
ac .
2. До азать, что
(a + b)(b + c)(a + c) l 8abc, если a l 0, b l 0, c l 0.
Р е ш е н и е. Имеем
a + b l 2
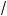 ab ; b + c l 2
ab ; b + c l 2
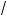 bc ; a + c l 2
bc ; a + c l 2
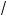 ac .
ac .
Все эти неравенства одина ово'о смысла с неотрицательными членами можно перемножить:
(a + b)(b + c)(a + c) l 2
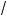 ab · 2
ab · 2
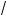 bc · 2
bc · 2
 ac ,
ac ,
или
(a + b)(b + c)(a + c) l 8abc.
3. До азать, что при любых значениях x и y верно неравенство
5x2 + 4xy + y2 + 2x > –5. (*)
125

Р е ш е н и е. Из данно'о неравенства следует: |
|
5x2 + 4xy + y2 + 2x + 5 > 0; |
|
(4x2 + 4xy + y2) + (x2 + 2x + 1) + 4 > 0; |
|
(2x + y)2 + (x + 1)2 + 4 > 0. |
(**) |
Полученное неравенство (**) верно, пос оль у (2x + y)2 l 0, (x + 1)2 l 0 и 4 > 0. Та а неравенство (**) верно, то и неравенство, из оторо'о оно получено, та же верно (на основании свойств неравенств); следовательно, верно и предшествующее неравенство, а значит, и данное неравенство (*), что и требовалось до азать.
5. Неравенства, содержащие переменную
1°. Решить неравенство, содержащее переменную, — значит найти множество значений переменной, при оторых данное неравенство является верным. Элементы это'о множества называют решениями неравенства.
2°. Два неравенства, содержащие одну и ту же переменную, называют равносильными, если они имеют общее множество решений, удовлетворяющих этим неравенствам (множества решений этих неравенств совпадают).
3°. Решение неравенств основано на их свойствах (см. п. 2). Используя эти свойства, можно сформулировать теоремы о равносильности неравенств (анало'ичные теоремам о равносильности уравнений).
4°. Если обеим частям неравенства f1(x) > f2(x) прибавить
(или вычесть) любую фун цию ϕ(x), область определения оторой принадлежит области определения данно о неравенства*, то получится новое неравенство, равносильное данному.
5°. Любое сла аемое, определенное для всех значений переменной, можно перенести из одной части неравенства в дру-ую, изменив зна это о сла аемо о на противоположный.
6°. Если обе части неравенства f1(x) > f2(x) умножить
(или разделить) на любую фун цию ϕ(x), определенную для всех значений переменной x из области определения данно о неравенства, сохраняющую постоянный зна и отличную от ну-
* Здесь и далее под областью определения неравенства будем понимать пересечение множеств, на оторых определена аждая из фун ций f1 и f2, входящих в неравенство.
126
ля, то при ϕ(x) > 0 получится неравенство, равносильное данному, а при ϕ(x) < 0 равносильным данному является неравенство противоположно о смысла.
6. Решение линейных и квадратных неравенств
1°. Линейным неравенством называют неравенство вида
ax + b > 0 (или ax + b < 0).
Если a > 0, то ax + b > 0 _ x > – b ;
--
a
если a < 0, то ax + b > 0 _ x < – b .
--
a
Пример. Решить неравенство 15 – 3x l 0.
Р е ш е н и е. Перенеся 15 в правую часть неравенства с противоположным зна ом, получим –3x l –15. Теперь разделим обе части последне'о неравенства на отрицательное число (–3) и изменим зна неравенства на противоположный: x m 5. Та-им образом, множеством решений данно'о неравенства служит луч (–×; 5].
2°. Квадратным неравенством называют неравенство вида
ax2 + bx + c > 0 (или ax2 + bx + c < 0).
Пусть требуется решить неравенство ax2 + bx + c > 0. В зависимости от зна а дис риминанта D = b2 – 4ac имеются три возможности.
1.Если D < 0, то 'рафи вадратно'о трехчлена f(x) = ax2 +
+bx + c не пересе ает ось Ox и лежит выше этой оси при a > 0 и ниже ее при a < 0. В первом случае множество решений неравенства есть вся числовая прямая (рис. 46, а), а во втором оно является пустым (рис. 46, б).
Рис. 46
127

Рис. 47
2. Если D > 0, то 'рафи вадратно'о трехчлена пересе ает ось Ox в точ ах x1 и x2 (x1 < x2), служащих орнями уравнения
ax2 + bx + c = 0. Эти точ и разбивают числовую прямую на три промежут а: (–×; x1), (x1; x2) и (x2; +×).
При этом зна вадратно'о трехчлена совпадает со зна омоэффициента a во всех точ ах промежут ов (–×; x1) и (x2; +×)
и противоположен зна у оэффициента a во всех точ ах промежут а (x1; x2) (рис. 47, а и б).
3. Если D = 0, то 'рафи вадратно'о трехчлена асается оси Ox точ е x1, являющейся единственным орнем уравнения ax2 + + bx + c = 0. Точ а x1 разбивает числовую прямую на два промежут а: (–×; x1) и (x1; +×). Зна вадратно'о трехчлена совпадает со зна ом оэффициента a при всех x − x1 (рис. 48, а и б).
Пример. Решить неравенство:
а) 2x2 – x – 1 > 0; б) x2 + 3x + 8 l 0; в) –3x2 + 10x – 3 > 0; ') 4x2 + 4x + 1 > 0.
Рис. 48
128

Ре ш е н и е. а) Здесь f(x) = 2x2 – x – 1, D = 1 – 4 · 2(–1) =
=9 > 0; (2x2 – x – 1 = 0) _ (x1 = –0,5, x2 = 1). В результате по-
лучаем три промежут а: (–×; –0,5), (–0,5; 1) и (1; +×). Таа a = 2 > 0, то f(x) > 0 в промежут ах (–×; –0,5) и (1; +×). Значит, решением данно'о неравенства служит объединение этих промежут ов: (–×; –0,5) (1; +×).
б) Здесь f(x) = x2 + 3x + 8, D = 9 – 32 = –21 < 0. Та а a = 1 > 0, то f(x) > 0 для всех x Ý R, т. е. неравенство справедливо на промежут е (–×; +×).
в) Здесь f(x) = –3x2 + 10x – 3, D = 100 – 4 · 9 = 64 > 0. Имеем
2 |
+ 10x – 3) = 0 |
_ |
|
x1 |
|
1 |
|
|
= 3 |
|
. Следовательно, получаем |
||
(–3x |
|
= -- ; x2 |
|
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
||
три промежут а: |
|
–×; |
1 |
, |
1 |
; 3 |
|
и (3; +×). Та а a = –3 < 0, |
|||||
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
то f(x) > 0 в промежут е |
1 |
; 3 |
|
. Ита , |
1 |
; 3 |
|
— решение дан- |
-- |
|
-- |
|
|||||
|
3 |
|
|
3 |
|
|
но'о неравенства.
') Здесь f(x) = 4x2 + 4x + 1, D = 16 – 16 = 0, (4x2 + 4x + 1 = = 0) _ (x1 = –0,5). Та а a = 4 > 0, то f(x) > 0 при всех x − 0,5. Значит, решением неравенства служит объединение промежут-ов: (–×; –0,5) (–0,5; +×).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Дайте определение неравенства.
2.Ка ие виды неравенств вы знаете?
3.Истинно ли выс азывание: а) 11 m 12; б) 11 m 11; в) x l y?
4.Запишите в виде двойно)о неравенства ((b < a) (b = a)) ∩
∩(a < c).
5.Сформулируйте свойства неравенств.
6.До ажите, что если a > b, то
ak > bk для любо)о натурально)о k.
7.До ажите, что 
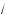 5 +
5 + 
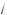 6 >
6 >
>
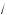 3 +
3 + 
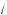 8 .
8 .
8. Можно ли неравенства 3 > –10 и –2 > –7 почленно: а) сложить; б) вычесть; в) умножить?
9. Дано числовое неравенство
12 > 5. Является ли верным неравенство: а) (a2 + 1) · 12 > 5(a2 + 1); б) 12a > 5a, если a < 0; в) 12|a| > > 5|a|; )) 12(1 – 2a + a2) > 5(1 – 2a +
+a2), если a − 1?
10.Что значит решить неравенство, содержащее переменную?
11.Ка ие неравенства называют равносильными?
12.Сформулируйте теоремы о равносильности неравенств.
129

|
13. Найдите множество реше- |
16. При а их значениях a |
||||||
ний неравенства: а) 6x – 5 l 7; |
уравнение ax2 – 6x + 1 = 0 имеет |
|||||||
|
3 |
|
x2 + 1 |
|
два различных действительных |
|||
б) |
1-----–------2----x-- |
< 0; в) |
--4-----–------x--- |
> 0; ) (2x – |
орня? |
|
|
|
|
|
|
17. Найдите множество зна- |
|||||
|
|
|
|
|
||||
– 1)2 + 2(x – 2)2 < (x – 2)(2x + 3) + |
чений k, при оторых уравнение |
|||||||
+ (2x + 1)2. |
|
|
4x2 + kx + 1 = 0 не имеет дейст- |
|||||
|
14. Решите )рафичес и нера- |
вительных орней. |
||||||
|
18. Найдите множество зна- |
|||||||
венство ax > 5. |
|
|
||||||
|
|
чений n, при оторых уравнение |
||||||
|
15. Решите )рафичес и нера- |
|||||||
|
6x – 1 |
|
x |
3 |
||||
|
|
|
|
|
|
|||
венство: а) x2 > 2x – 1; б) x2 < 6 – |
--n------–-----2---- |
+ |
n------+-----2-- |
= n------+------2- имеет ре- |
||||
– 5x. |
|
|
|
шение x > –2. |
|
|||
УПРАЖНЕНИЯ
1. Решите неравенство:
а) ax – 3 < 2x + 1; б) x + 4 > nx – 7; в) 3 – ax < 2x + 1. 2. Решите неравенство:
а) (---76-------x-----–------532-----------)--3---(--1-----–-----x-----)--2- |
< 0; |
б) (---3-----–-----x----)--2---(---2-----–-----x----)--2- |
> 0. |
(3x – 20)2 |
|
( 5x – 8)3 |
|
3. До ажите, что:
а) (x + y)2 l 4xy; б) x3 + y3 l x2y + xy2 (x > 0, y > 0);
в) -----2----a------- |
m 1; ') |
ab l |
----2----a---- |
(a > 0, b > 0); |
|||
a2 + 1 |
|
|
|
|
a + b |
|
|
2 |
|
2 |
l |
12ab; е) |
a2 + 1 |
l 2; |
|
д) 3a + 12b |
|
------a----2----- |
- |
||||
|
|
|
|
|
|
|
|
ж) (a + 1)(b + 1)(a + c)(b + c) > 16abc, 'де a > 1, b > 1, c > 1; з) 5x2 + 4xy + y2 + 2x > –5; и) x2 + 2y2 + 2xy + 6y + 10 l 0. 4. Решите неравенство:
а) (---x-----–-----3----)---(--x----2----+------3----x-----+------9----) m 0; б) -------- |
-----x-----2---+-----3----x-----+------9----- |
-------- l 0; |
|
|
||
x2 – 2x + 4 |
(x |
+ 2)( x2 – 2x + 4) |
|
|
||
в) x-----2----+-----4----x-----+------4-- m 0; ') x-----2----–-----6----x-----+-----9-- |
> 0; д) (---x-----+------3----)--4---(--x------–-----4----) |
< 0. |
||||
x2 + 5x + 7 |
x2 + 3 |
|
(2 – x)2 |
|
|
|
5. Решите неравенство: |
|
|
|
|
|
|
а) ---2----x----2----+------x-----–-----1---- > 0; б) |
--x----4----+-----x----2----+------3--- |
l 0; в) x------4---–-----3----x----3----+-----2----x----2- |
m 0. |
|||
– x2 + 5x – 7 |
– x2 + x + 2 |
|
x2 – x + 20 |
|
|
|
6. Найдите наименьшее целое числа, принадлежащее области определения фун ции:
а) y = x + ----15--------- |
; б) y = |
4 – --3--- ; в) y = (9 – x2)–1 . |
x + 2 |
|
x2 |
130
