Готовимся к экзамену по математике_Крамор В.С_2008 -544с

12. Наименьшее общее кратное

1°. Рассмотрим множество A чисел, ратных 4, и множество B чисел, ратных 6, т. е. A = {4; 8; 12; 16; 20; ...}; B = {6; 12; 18; 24; ...}. Числа 12, 24, 36, ... являются ратными чисел 4 и 6. Их называют общими ратными чисел 4 и 6. Множество C общих ратных есть пересечение множеств A и B, т. е. C = A ∩ B.

2°. Наименьший элемент множества C называют наимень-

11

УПРАЖНЕНИЯ

1.До ажите, что одно из двух последовательных четных чисел делится на 4 нацело.

2.До ажите, что разность ab – ba ратна 9.

3.До ажите, что вся ое трехзначное число, записанное одина овыми цифрами, делится нацело на 37.

4.Ка ой цифрой о анчивается произведение

51 · 52 · 53 ... 58 · 59?

5. До ажите, что сумма двузначно о числа и числа, записанно о теми же цифрами, но в обратном поряд е, ратна 11.

12

6.Сумма цифр двузначно о числа равна 6. Если этому числу прибавить 18, то получится число, записанное теми же цифрами, но в обратном поряд е. Найдите исходное число.

7.Найдите двузначное число, равное сумме вадрата числа единиц и числа десят ов.

8.Остато от деления натурально о числа k на 12 равен 5, а остато от деления числа k на 16 равен 9. Чему равен остато от деления наименьше о из возможных значений k на 24?

9.Найдите двузначное число, равное утроенной сумме е о цифр.

О Т В Е Т Ы

4. 0. 6. 24. 7. 89. 8. 17. 9. 27.

Решения и методичес ие у азания

К упражнению 1

1.Ка известно, число называется четным, если оно делится на 2 нацело.

2.Формула четно"о числа имеет следующий вид: а) 2n; б) 2n – 2; в) 2n + 2.

3.Пусть n Ý N. То"да 2n — четное число, а 2n + 2 — следующее четное число.

4.Если n = 2k, "де k Ý N, то число 2n = 2 · 2k = 4k делится на 4 на-

цело.

5.Если n = 2k – 1 (нечетное), "де k Ý N, то число 2n + 2 = 2(2k – 1) +

+2 = 4k – 2 + 2 = 4k делится на 4 нацело.

К упражнению 2

1. Имеем ab = 10a + b (двузначное число, "де a — цифра десят ов,

b — цифра единиц); анало"ично ba = 10b + a. 2. Следовательно,

ab – ba = 10a + b – (10b + a) = 9a – 9b = 9(a – b). 3. Число 9(a – b) делится на 9 нацело.

К упражнению 3

1. Трехзначное число, записанное одина овыми цифрами, имеет вид aaa .

13

2.Имеем aaa = 100a + 10a + a = 111a.

3.Число 111 делится на 37 нацело; следовательно, и число 111a делится на 37.

К упражнению 4

1.Среди данных множителей выделим две пары множителей: 52 и 55; 55 и 56.

2.Если мы умножим 52 на 55 или 55 на 56, то произведение будет о анчиваться нулем.

3.Та им образом, произведение остальных множителей на 52 · 55 или 55 · 56 будет о анчиваться нулем.

К упражнению 5

1.Имеем ab = 10a + b; анало"ично ba = 10b + a.

2.Следовательно, сумма

ab + ba = 10a + b + 10b + a = 11a + 11b = 11(a + b)

делится на 11 нацело.

К упражнению 6

1.Пусть x — цифра десят ов, а y — цифра единиц исходно"о числа.

2.Поэтому исходное число можно записать в виде 10x + y.

3.То"да задача сводится решению системы уравнений

x + y = 6,

10x + y + 18 = 10y + x.

4. Решив эту систему, получим x = 2, y = 4. Ита , исходное число есть 24.

К упражнению 7

1.Пусть ис омое число имеет вид 10a + b.

2.То"да в силу условия имеем

10a + b = a + b2,

от уда 9a = (b – 1)b.

3.Ясно, что произведение b(b – 1) должно быть ратно 9.

4.Та а b m 9, а b – 1 m 8, то b(b – 1) делится на 9 лишь то"да,о"да b = 9.

5.Следовательно, 9a = 9 · 8, от уда a = 8. Ита , ис омое число есть 89.

14

К упражнению 8

1.Пусть k — натуральное число, p и q — целые части от деления k на 12 и 16 соответственно.

2.То"да, со"ласно условию, имеем систему

k = 12p + 5, k = 16q + 9.

3. Левые части этих соотношений равны, поэтому равны и правые части, т. е.

5.Та а в равенстве (2) p и q — целые положительные числа, то

спомощью перебора устанавливаем, что наименьшему значению q = 2 соответствует целое p = 3.

6.Та им образом, наименьшее значение k = 41, а остато от деления 41 на 24 равен 17.

4.Та а в равенстве (2) a и b — натуральные числа, меньшие 10, то перебором устанавливаем, что наименьшему значению b = 7 соответствует целое a = 2.

5.Та им образом, ис омое число есть 27.

15

Т е м а 2

À

Обыкновенные дроби. Правильные и неправильные дроби. Основное свойство дроби. Сравнение дробей.

Сокращение дроби. Сложение и вычитание дробей. Умножение дробей. Деление дробей. Десятичные дроби. Обращение десятичной дроби в обыкновенную

и обыкновенной в десятичную. Периодические дроби. Отношение. Пропорция. Свойства пропорций.

Свойства отношений. Процент.

Основные задачи на проценты. Деление числа на части, прямо и обратно пропорциональные данным числам

Теоретичес ие сведения

1. Обыкновенные дроби

1°. Одну или нес оль о равных частей единицы называют

обы новенной дробью.

1

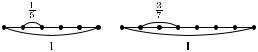
Например, дробь -- означает, что единица разделена на

5

2

5 равных частей и взята та ая одна часть; дробь -- означает,

7

что единица разделена на 7 равных частей и взяты две та ие части (рис. 3).

2°. Обы новенная дробь записывается с помощью черты и двух натуральных чисел. Число, записанное под чертой и по-азывающее, на с оль о равных частей разделена единица, называют знаменателем дроби. Число, записанное над чертой и по азывающее, с оль о взято та их равных частей, называют числителем дроби.

Рис. 3

16

3°. Из определения дроби следует что дробную черту можно

2

рассматривать а зна деления. Например, -- = 2 : 7.

7

Та им образом, дробь, у оторой числитель равен знамена-

5

телю, равна единице. Например, -- = 1.

5

2. Правильные и неправильные дроби

1°. Дробь, в оторой числитель меньше знаменателя, назы-

3

вают правильной. Например, -- — правильная дробь.

8

2°. Дробь, в оторой числитель равен знаменателю или

3 5

больше е$о, называют неправильной. Например, -- , -- — не-

3 2

правильные дроби.

3°. Число, состоящее из натурально$о числа и дроби, назы-

2°. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной. Это свойство называют основным свой-

17

4. Сравнение дробей. Сокращение дроби

3°. Для сравнения дробей с разными числителями и знаменателями их предварительно приводят общему знаменателю или общему числителю.

4°. Деление числителя и знаменателя на их общий делитель называют со ращением дроби. При этом получается дробь, равная данной.

5. Сложение и вычитание дробей

1°. При сложении дробей с одина овыми знаменателями числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель. Полученную дробь, если это возможно, со ращают. Например,

2°. Наименьшим общим знаменателем двух или нес оль-их дробей является наименьшее общее ратное знаменателей этих дробей.

При сложении дробей с различными знаменателями нужно предварительно привести их наименьшему общему знаменателю. Например,

3°. При вычитании смешанных чисел из целой части уменьшаемо$о вычитают целую часть вычитаемо$о, а из дробной части уменьшаемо$о — дробную часть вычитаемо$о. Например,

18

4°. Если дробная часть вычитаемо$о больше дробной части уменьшаемо$о, то одну из единиц целой части уменьшаемо$о нужно заменить равной ей дробью. Например,

Анало$ично выполняется сложение смешанных чисел. Заметим, что вычитание дробей может привести понятию

отрицательной дроби. Этот случай будет рассмотрен в теме 3.

6. Умножение дробей

оторой равен произведению числителей, а знаменатель — про-

но$о числа, разделив числитель на знаменатель и выделив це-

ными, та а их произведение равно 1.

7. Деление дробей

1°. При делении дроби на дробь числитель делимо$о умножают на знаменатель делителя, а знаменатель делимо$о — на числитель делителя. Первое произведение служит числителем,

19

а второе — знаменателем частно$о. Например,

2°. При делении смешанных чисел нужно предварительно представить их в виде дробей и применить правило деления дроби на дробь. Например,

ние и деление цело$о числа на дробь (или наоборот). Например,

8. Десятичные дроби

1°. Обы новенную дробь, знаменатель оторой равен 10, 100, 1000 и т. д. (т. е. изображен единицей с нулями), называют де-

и т. д.

2°. Сложение и вычитание десятичных дробей. При сложении (вычитании) десятичных дробей числа записывают та , чтобы одина овые разряды были помещены один под дру$им, а запятая — под запятой, и с ладывают (вычитают) а натуральные числа.

В ответе а при сложении, та и при вычитании ставят запятую под запятой соответственно в сла$аемых и в уменьшаемом и вычитаемом. Например:

3°. Умножение десятичных дробей. Чтобы умножить одну десятичную дробь на дру$ую, надо выполнить умножение, не обращая внимания на запятые, и в полученном произведении

20