
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
4.При а ом значении ар'умента x фун ция y = x2 – 2x – 15 принимает наименьшее значение?
5.До ажите, что фун ция, заданная формулой y(x) = 3x2, 'де x m 0, — убывающая.
6.При а ом значении ар'умента x фун ция y = x2 – 4x + 4 принимает наименьшее значение?
7.Решите уравнение:
а) 2(x – 3) + |x + 2| = 1; б) |2x + 5| – |3x – 4| = 3 – 2x;
в) x – 2 + |
x – 1 + |
x – 3 + 1 = 0; ') a------+-----5-- |
= a; |
|||||
|
|
|
|
|
|
|
x – 3 |
|
д) |
------b------- |
= 2; |
е) a2x – a = 4x + 2; |
ж) x + --3--- = --1--- (9x + 1); |
||||
|
x + 1 |
|
|
|
|
|
a3 |
a2 |
з) |2x – 5| – |3x – 4| = 3 – 2x; и) x – 2 + 1 – x = 2. |
||||||||
8. Установите, равносильны ли уравнения: |
|
|||||||
а) (x – 2)2 = 3(x – 2) и x – 2 = 3; |
|
|
||||||
б) x------+-----3-- |
= 2----x------–-----1- |
и x + 3 = 2x – 1; |
|
|
||||
|
x + 1 |
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
в) x – 2 = 2 – x и x – 2 + x-----2----+-----1-- = 2 – x + x-----2----+-----1-- |
; |
|||||||
') 5 – 3x – ------ |
1------- |
= 2x – |
------1------- |
и 5 – 3x = 2x; |
|
|||
|
|
x |
– 1 |
|
x – 1 |
|
|
|
д) (x + 3)(x – 3) = 0 и x + 3 = 0;
е) x2 = 2x – 1 и x2(x4 + 1) = (2x – 1)(x4 + 1).
Задания для повторения
9.Имеется усо сплава меди с оловом массой 12 ', содержащий 45% меди. С оль о чисто'о олова надо прибавить
этому сплаву, чтобы получившийся новый сплав содержал 40% меди?
10.Свежие 'рибы содержат 90% воды, а сухие — 12%. Из а о'о оличества свежих 'рибов можно получить 450 ' сухих?
11.Первый турист, проехав 1,5 ч на велосипеде со с оростью 16 м/ч, делает останов у на 1,5 ч, а затем продолжает ехать с первоначальной с оростью. Через 4 ч после отправления в доро'у перво'о туриста вдо'он у ему выезжает на мотоци ле второй турист со с оростью 56 м/ч. Ка ое расстояние они проедут, прежде чем второй турист до'онит перво'о?
81

12. Трое мальчи ов получили за свою работу возна'ражде-
ние в размере 1410 р., причем второй получил 1 то'о, что по-
--
3
лучил первый, и еще 60 р., а третий получил |
1 |
дене' второ'о |
-- |
||
|
3 |
|
и еще 30 р. С оль о дене' получил аждый? |
|
|
О Т В Е Т Ы
1. а) Четная; б) нечетная; в) ни четная, ни нечетная; >) ни четная, ни нечетная. 2. а) Четная; б) нечетная; в) нечетная; >) четная; д) ни четная, ни нечетная; е) нечетная; ж) ни четная, ни нечетная; з) четная; и) нечетная; ) ни четная, ни нечетная; л) ни четная, ни нечетная.
4. При x = 1. |
6. При x = 2. |
5 |
2 |
; в) нет орней; >) единствен- |
7. а) x = -- |
; б) -- |
|||
|
|
3 |
7 |
|
ный орень x = 4a + 5 , если a − 0, a − –5; нет орней, если a = 0, a = –5;
-----------------
a
д) единственный орень x = b-----–-------2 , если b − 0; нет орней, если b = 0; |
||
|
2 |
|
е) единственный орень x = |
------1------ |
, если a − –2, a − 2; x Ý R, если a = –2; |
|
a – 2 |
|
|
|
1 |
нет орней, если a = 2; ж) единственный орень x = a----(----a----+------3----) , если a − 0, |
||
a − –3, a − 3; x Ý R, если a = 3; нет орней, если a = 0, a = –3;
з) x Ý |
2 |
; 2 |
|
; и) нет орней. 8. |
а) Нет; б) да; в) да; >) нет; д) нет; е) да. |
-- |
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
9. 1,5 >. 10. 3960 >. 11. 56 м. 12. 900 р; 360 р.; 150 р.
Решения и методичес ие у азания
К упражнению 1а
1.Напомним, что фун цию y = f(x), x Ý X, называют четной, если: а) X — симметричное множество;
б) для любо>о x Ý X выполняется равенство f(–x) = f(x).
2.Областью определения фун ции y = x6 служит вся числовая прямая (–×; +×) — симметричное множество.
3.Имеем f(x) = x6, f(–x) = (–x)6 = x6. Та им образом, f(–x) = f(x),
т.е. фун ция y = x6 является четной.
К упражнению 1б
1. Напомним, что фун ция y = f(x), x Ý X, называют нечетной, если: а) X — симметричное множество;
б) для любо>о x Ý X выполняется равенство f(–x) = –f(x).
82

2.Областью определения фун ции y = x7 является вся числовая прямая (–×; +×) — симметричное множество.
3.Имеем f(x) = x7, f(–x) = (–x)7 = –x7. Значит, f(–x) = –f(x), т. е. фун ция y = x7 является нечетной.
К упражнению 1в
1. Фун ция y = x – 2 не определена при тех значениях x, для о-
----------------
x2 – 9
торых знаменатель x2 – 9 обращается в нуль, т. е. в точ ах ä3. Значит, область определения фун ции — симметричное множество.
2. |
Имеем |
|
|
|
f(x) = --x-----–-----2---- , f(–x) = |
--(--–----x----)----–-----2--- = –--x-----+-----2---- . |
|
|
x2 – 9 |
(–x)2 – 9 |
x2 – 9 |
3. |
Та а f(–x) − f(x) и f(x) − –f(x), то фун ция не является ни |
||
четной, ни нечетной. |
|
|
|
К упражнению 1 |
|
|
|
1. |
Область определения фун ции y = |
x – 3 есть луч [3; +×) — |
|
несимметричное множество. |
|
|
|
2. |
Следовательно, фун ция не является ни четной, ни нечетной. |
||
К упражнению 3 |
|
|
|
1. |
Пусть x2 > x1, >де x2 > 0, x1 l 0. То>да |
||
|
f(x2) – f(x1) = 3x22 – 3x12 = 3(x22 – x12 ) = |
||
=3(x2 – x1)(x2 + x1) > 0.
2.Следовательно, x2 > x1 l 0 ^ f(x2) > f(x1), т. е. большему значе-
нию ар>умента x Ý D(f) соответствует большее значение фун ции. 3. Ита , фун ции f(x) — возрастающая.
К упражнению 4
1. Преобразуем данный вадратный трехчлен:
x2 – 2x – 15 = (x2 – 2x + 1) – 1 – 15 = (x – 1)2 – 16.
2.Выражение (x – 1)2 – 16 принимает наименьшее значение при том же значении x, что и (x – 1)2.
3.Та а (x – 1)2 l 0 при любом x, то наименьшее значение фун ция (x – 1)2, а значит, и данная фун ция принимает при x = 1.
83

К упражнению 7б
1. Найдем орни двучленов, записанных под зна ом модуля:
2x + 5 = 0 |
5 |
; 3x – 4 = 0 |
4 |
^ x = –-- |
^ x = -- . |
||
|
2 |
|
3 |
2. Изобразим эти орни на оординатной прямой (рис. 16) и рассмотрим данное уравнение на аждом из трех промежут ов:
Рис. 16 |
5 |
5 |
4 |
4 |
|
x < –-- |
, –-- |
m x < -- |
, x l -- . |
|
2 |
2 |
3 |
3 |
3. В первом промежут е получаем систему
5 |
, |
|
5 |
, |
x < –-- |
|
x < –-- |
||
2 |
|
или |
2 |
|
|
|
|
|
|
–(2x + 5) + (3x – 4) = 3 – 2x, |
|
x = 4. |
|
|
Эта система не имеет решений.
4. Далее, во втором промежут е получаем систему
|
|
|
|
|
|
|
5 |
|
m x < |
4 |
, |
|||
|
5 |
|
4 |
|
|
–-- |
|
-- |
||||||
|
–-- |
m x < |
-- |
, |
|
2 |
|
|
|
|
3 |
|
||
2 |
|
3 |
или |
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2x + 5 + (3x – 4) = 3 – 2x, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
-- |
|
|
|
|
|||||
|
|
|
|
|
2 |
|
x = |
7 . |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решением этой системы является x = -- . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
5. На онец, в третьем промежут е получаем систему |
|
|||||||||||||
|
|
|
4 |
|
|
|
|
|
x l |
4 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x l -- , |
|
|
|
|
|
-- |
|
|
|||
|
|
|
3 |
|
или |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2x + 5 – (3x – 4) = 3 – 2x, |
|
|
x = –6, |
|
|
||||||
оторая не имеет решений.
6. Ита , x = 2 — орень данно>о уравнения.
--
7
К упражнению 7в
1. Найдем область определения уравнения:
 x – 2 l 0,
x – 2 l 0,

 x – 1 l 0, ^ x l 3. x – 3 l 0
x – 1 l 0, ^ x l 3. x – 3 l 0
2.Если x = 3, то 
 1 +
1 + 
 2 +
2 + 
 0 + 1 > 0.
0 + 1 > 0.
3.Если x > 3, то выражение, получающееся в левой части уравнения, подавно больше нуля.
4.Ита , множество решений данно>о уравнения является пустым.
84

К упражнению 7 |
|
|
|
|
|
1. Имеем |
|
|
|
|
|
a-----+------5-- – a = 0, или |
4----a-----–------ax---------+-----5-- |
= 0, >де x − 3. |
|
||
x – 3 |
|
|
x – 3 |
|
|
2. Решим систему |
|
ax = 4a + 5, |
|
|
|
|
|
|
|||
|
|
|
|||
|
x − 3. |
|
|
|
|
|
|
|
|
||
а) Если a − 0, то x = 4a + 5 ;----------------- |
|
|
|
||
|
|
a |
|
|
|
б) если a = 0, то получаем 0 · x = 5, что ложно. |
|
||||
3. Найдем, на онец, значение a, при отором x = 3; имеем 4----a-----+------5-- |
= 3, |
||||
|
|
|
|
a |
|
от уда a = –5.
Ита , получаем ответ: уравнение имеет единственный орень x =
= 4a + 5 , если a − 0, a − –5; уравнение не имеет орней, если a = 0,
-----------------
a a = –5.
К упражнению 9
1.Исходный сплав массой 12 > содержал 45% меди, т. е. в нем было 0,45 · 12 > меди.
2.Пусть x ( >) — масса олова, добавленно>о данному сплаву. То>да получится сплав массой 12 + x ( >), содержащий 40% меди.
3.Значит, в новом сплаве имеется 0,4(12 + x) > меди.
4.Та а масса меди и в первоначальном, и в новом сплаве одна
ита же, то приходим уравнению
0,4(12 + x) = 0,45 · 12.
5. Решив это уравнение, находим x = 1,5. Ита , первоначальному сплаву надо добавить 1,5 > олова.
К упражнению 10
1.В 450 > сухих >рибов содержится 12% воды и 88% сухой массы.
2.Значит, сухая масса равна 88%(450 >) = 396 >.
3.Эту же сухую массу должны иметь и положенные на суш у свежие >рибы, массу оторых обозначим через x.
4.Следовательно, получаем уравнение
10%(x) = 396, т. е. 0,1x = 396,
от уда x = 3960 >.
85
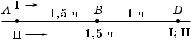
К упражнению 11
1.Со>ласно условию, первый турист выехал на 4 ч раньше второ>о.
2.В точ е B (рис. 17) он сделал останов у на 1,5 ч.
Рис. 17
3.Второй турист до>нал перво>о в точ е D.
4.Чтобы преодолеть расстояние AD, первый турист затратил на 2,5 ч больше, чем второй (та а 4 – 1,5 = 2,5).
5.Пусть s ( м) — расстояние от точ и A до точ и D.
6. То>да t1 = |
s |
(ч) — время, за оторое первый турист проехал |
|
------ |
|||
|
16 |
|
|
расстояние AD; t2 = |
s |
(ч) — время, за оторое второй турист проехал |
|
------ |
|||
|
|
56 |
|
расстояние AD. Ка мы установили, t1 – t2 = 2,5 (ч). 7. Та им образом, получаем уравнение
s |
– |
s |
= 2,5, |
------ |
------ |
||
16 |
|
56 |
|
от уда находим s = 56 ( м). |
|
|
|
|
||
К упражнению 12 |
|
|
|
|
||
1. |
Пусть первый мальчи получил x р. |
|||||
2. |
То>да второй получил |
1 |
x + 60 |
р., а третий получил |
||
-- |
||||||
|
|
|
3 |
|
|
|
+ 60 + 30 = -- |
x + 50 р. |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
9 |
|
|
|
|
|
3. |
Из условия следует, что |
|
|
|
|
|
|
|
1 |
|
1 |
x + 50 = 1410, |
|
|
|
x + -- x + 60 + -- |
||||
|
|
3 |
|
9 |
|
|
1 1 x +
-- --
3 3
от уда x = 900.
Ответ: 900 р.; 360 р.; 150 р.
86
Т е м а 7
À
Линейная функция и ее график. Квадратичная функция и ее график.
k
Функция y = -- и ее график. x
Дробно/линейная функция и ее график. Квадратные уравнения. Теорема Виета. Графический способ решения квадратных уравнений. Уравнения с несколькими переменными.
Системы уравнений
Теоретичес ие сведения
1. Линейная функция и ее график
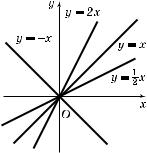
1°. Фун цию, заданную формулой y = kx + b, 'де k и b — не-оторые числа, называют линейной.
2°. Областью определения линейной фун ции служит множество R всех действительных чисел, та а выражение kx + b имеет смысл при любых значениях x.
3°. Графи линейной фун ции y = kx + b есть прямая. Для построения 'рафи а, очевидно, достаточно знать две е'о точ и,
например A(0; b) и B |
|
b |
; 0 |
|
. |
|
–-- |
|
|||
|
k |
|
|
4°. Коэффициент k хара теризует у'ол, оторый образует прямая с положительным направлением оси Ox (рис. 18); поэтому k называют ловым оэффициентом. Если k > 0, то этот у'ол — острый, если k < 0 — тупой; если k = 0, то прямая параллельна оси Ox.
5°. Графи фун ции y = kx + b можно та же построить с помощью параллельно'о переноса 'рафи а фун - ции y = kx.
Рис. 18 |
87
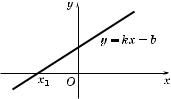
Рис. 19 |
6°. Уравнение вида kx + b = 0 называют линейным. Для то'о чтобы решить линейное уравнение 'рафичес и, достаточно построить 'рафи фун ции y = kx + b и найти точ у е'о пересечения с осью Ox (на рис. 19 точ а x1 — орень
уравнения).
2. Квадратичная функция и ее график
1°. Фун цию, заданную формулой y = ax2 + bx + c, 'де x, y — переменные, a, b и c — не оторые числа, причем a − 0, называют вадратичной.
2°. Областью определения вадратичной фун ции является множество R.
3°. Графи ом фун ции y = ax2 + bx + c является парабола —
ривая, симметричная относительно прямой x = – b , прохо-
------
2a
дящей через вершину параболы (вершиной параболы называют точ у пересечения параболы с ее осью симметрии).
4°. Координаты вершины параболы определяются по формулам
x0 = – |
---b--- |
; y0 = f(x0) = |
4----ac---------–-----b---2- . |
|
2a |
|
4a |
5°. Квадратичную фун цию y = ax2 + bx + c все'да можно привести виду y = a(x + k)2 + p, а затем построить ее 'рафи с помощью 'еометричес их преобразований.
6°. При a > 0 ветви параболы направлены вверх, а при a < 0 — вниз.
Пример. Построить 'рафи фун ции y = 3x2 + 12x + 10.
Р е ш е н и е. Выделив из вадратно'о трехчлена вадрат двучлена, получим
3x2 + 12x + 10 = 3(x2 + 4x) + 10 =
= 3(x2 + 4x + 4) – 12 + 10 = 3(x + 2)2 – 2.
Строим сначала 'рафи фун ции 3x2, а затем, используя параллельный перенос, получим ис омый 'рафи — параболу с вершиной в точ е (–2; –2) (рис. 20).
88
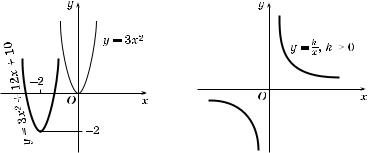
Заметим, что параболу можно построить и по та называемым хара теристичес им точ ам, т. е. по оординатам вершины и точ ам пересечения с осями оординат, о чем будет с азано в дальнейшем.
k
3. Функция y = -- и ее график x
1°. Если переменная y пропорциональна переменной x, то та-ая зависимость выражается формулой y = kx, 'де k − 0 — оэффициент пропорциональности. Графи этой фун ции мы рассмотрели в п. 1.
2°. Если переменная y обратно пропорциональна переменной
x, то та ая зависимость выражается формулой y = k , 'де k − 0 —
--
x
оэффициент обратной пропорциональности.
3°. Область определения фун ции y = k есть множество
--
x
всех чисел, отличных от нуля, т. е. (–×; 0) (0; +×).
4°. Графи ом обратной пропорциональности y = k является
--
x
ривая, состоящая из двух ветвей, симметричных относительно оординат. Та ую ривую называют иперболой (рис. 21). Если k > 0, то ветви 'иперболы расположены в I и III оординатных четвертях; если же k < 0 — во II и IV четвертях.
5°. Заметим, что 'ипербола не имеет общих точе с осямиоординат, а лишь нео'раниченно ним приближается (объясните, почему).
Рис. 20 |
Рис. 21 |
89
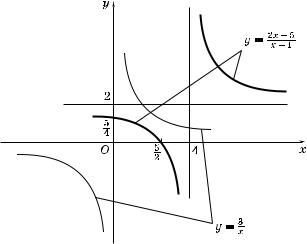
4. Дробно;линейная функция и ее график
1 |
° |
. Фун цию вида y = |
ax + b |
|
'де a |
− 0, c |
− 0, |
b |
− |
d |
назы- |
||||
|
cx---------+------d- |
|
-- |
-c- |
|||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
||||
вают дробно-линейной. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2°. Преобразуем эту фун цию следующим образом: |
|
||||||||||||||
|
|
a |
(cx + d) + b – |
ad |
|
|
|
b – |
ad |
|
|
bc – ad |
|||
|
|
-- |
------ |
|
|
|
------ |
|
|
------------------- |
|||||
---------------- -----y = ax + b = c |
---------------------------- |
----------- |
--c---- |
= a-- |
+ |
----------- |
--c--- |
= a-- |
+ |
------- |
-c---2-------- . |
||||
|
|
cx + d |
cx + d |
|
|
c |
|
cx + d |
c |
|
x + d-- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
С помощью 'еометричес их преобразований 'рафи дробно-
линейной фун ции можно получить из 'рафи а фун ции y = -k- . |
||||
|
|
|
|
x |
Пример. Построить 'рафи фун ции y = |
2----x------–-----5- . |
|||
|
|
|
x – 4 |
|
Р е ш е н и е. Преобразуем заданную фун цию та : |
||||
y = 2----x-----–------5- |
= 2----(---x-----–-----4----)----–-----5-----+------8- |
= 2 + |
------3------- |
. |
x – 4 |
x – 4 |
|
x – 4 |
|
Сначала строим 'рафи фун ции y = |
-3- ; затем смещаем е'о на |
|||
|
|
x |
|
|
4 ед. вправо вдоль оси Ox и на 2 ед. вверх вдоль оси Oy (рис. 22).
Рис. 22 |
90
