
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
Примеры. 1. Решить систему уравнений
 2x · 3y = 24,
2x · 3y = 24,
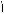 2y · 3x = 54.
2y · 3x = 54.
Р е ш е н и е. Запишем данную систему в виде
|
2x · 3y = 23 · 3, |
(*) |
|
||
|
||
|
2y · 3x = 2 · 33. |
(**) |
|
||
|
||
Перемножив уравнения (*) и (**), получим |
|
|
2x + y · 3x + y = 24 · 34 _ 6x + y = 64 _ x + y = 4.
Разделим почленно уравнение (*) на уравнение (**):
|
|
|
|
2x – y |
22 |
2x – y · 3y – x = 22 · 3–2 _ ------------- = |
----- _ |
||||
|
|
|
|
3x – y |
32 |
2 x – y |
|
2 |
2 |
|
|
_ 3-- - |
= |
3-- |
_ x – y = 2. |
||
Решив теперь систему x + y = 4, x – y = 2, получаем ответ: |
|||||
x = 3, y = 1. |
|
|
|
|
|
2. Решить систему уравнений |
|
|
|||
|
(x – y)0,5y – x = 5 · 2x – y, |
|
|||
|
|
||||
|
|
x + y |
|
|
|
|
(x – y ) |
------------- |
|
|
|
|
7 |
= 125. |
|
||
|
|
|
|
|
|
Р е ш е н и е. Перепишем первое уравнение системы в виде (x – y)2x – y = 5 · 2x – y; разделив обе части это о уравнения на 2x – y − 0, получим x – y = 5.
Подставив теперь во второе уравнение системы вместо разности x – y ее значение, равное 5:
x + y |
= 125 _ 5 |
x + y |
= 53 _ x + y = 3 _ x + y = 21. |
5 7 |
7 |
||
------------- |
|
------------- |
|
|
|
|
7 |
Остается решить систему уравнений x – y = 5, x + y = 21;
врезультате получаем ответ: x = 13, y = 8.
3.Решить систему неравенств
2 |
x |
· |
8 |
–x |
27 |
, |
3 |
|
9 |
|
64 |
||
-- |
|
-- |
|
> ------ |
2x2 – 6 x – 3,5 < 8 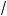 2 .
2 .
191

Р е ш е н и е. Имеем
|
|
|
|
2 |
|
x |
· |
8 |
|
–x |
27 |
, |
|
|
3 |
|
x |
> |
3 |
|
3 |
|||
|
|
|
-- |
|
-- |
> |
------ |
|
-- |
|
-- |
, |
||||||||||||
|
|
|
|
3 |
|
|
|
9 |
|
|
64 |
_ |
|
|
4 |
|
|
|
4 |
|
_ |
|||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2x2 – 6 x – 3,5 |
< 8 |
2 |
|
|
2x2 – 6 x – 3,5 |
< 23,5 |
|||||||||||||||
_ |
|
x < 3, |
|
|
|
|
|
|
|
|
|
x < 3, |
|
|
|
|
|
|
|
|
|
x < 3, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x2 – 6x – 3,5 < 3,5 _ |
|
x2 – 6x – 7 < 0 _ |
|
|
(x + 1)(x – 7) < 0. |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
Ита , интервал (–1; 3) — решение данной системы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Ка ую фун цию называют по азательной?
2.Что является областью определения и множеством значений по азательной фун ции?
3.Что понимают под степенью с иррациональным по азателем? Приведите примеры.
4.Перечислите свойства
фун ции y = ax при a > 1.
5.Перечислите свойства фун ции y = ax при 0 < a < 1.
6.До ажите, что фун ция
y = 2x является возрастающей. 7. Постройте )рафи и фун -
ций: а) y = |
|
2 |
|
x |
|
и |
|
y = 1,5x; |
-- |
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
б) y = 0,75x и y = |
|
4 |
|
x |
||||
-- |
. Ка ово |
|||||||
|
|
|
|
|
|
3 |
|
|
их взаимное расположение?
8. С помощью а о)о преобразования плос ости можно получить )рафи фун ции y = 0,5x из )рафи а фун ции y = 2x?
9. С оль о точе пересечения имеют )рафи и фун ций y = 2x и y = 0,28x?
10. Ка ое за лючение можно сделать о зна е числа x, если 3x = 0,9?
11.Ка ое уравнение называют по азательным?
12.Почему при решении по-азательных уравнений пола)а- ют, что a > 0, a − 1?
13.Дано уравнение вида
af(x) = 1. Можно ли утверждать, что f(x) = 0?
14.Дано уравнение вида af(x) = ak. Ко)да можно утверждать, что f(x) = k?
15.Дано уравнение вида
Aa2x + Bax + C = 0. С помощьюа ой подстанов и оно сведетсявадратному уравнению?
16. Уравнение вида Aax + + Bax/ 2 · bx/ 2 + Cbx = 0 преобразуйте вадратному уравнению.
17. Решите )рафичес и уравнение: а) 2x = 6; б) 2x = 3x; в) 0,2x = 0,7x.
18.Ка ое неравенство называют по азательным?
19.Дано неравенство вида
af(x) < ag(x). Можно ли утверждать, что: а) f(x) < g(x); б) f(x) > g(x)?
20. Ка ие свойства по азательной фун ции применяются
192

при решении неравенства: а) 2x >
> 2 |
m |
; б) |
1 |
x |
< |
1 |
n |
? |
|
-- |
|
-- |
|
||||
|
|
|
3 |
|
3 |
|
|
|
|
21. Используя свойства по а- |
|||||||
зательной фун ции: |
|
|||||||||
|
|
|
а) сравните |
|
с |
единицей: |
||||
|
1 |
|
3 |
; ( |
|
3) |
1 / 2 |
; |
(0,9)– 5 ; n–2/3; |
|
|
|
|||||||||
-- |
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
2 |
n |
1 |
|
1/4 |
|
|
|
|||
|
-- |
|
; |
-- |
|
|
; |
|
|
|
5 |
|
4 |
|
|
|
|
|
|||
|
б) сравните |
|
значения |
выра- |
||||||||||
жений: n– |
|
3 и |
|
1 |
|
– |
3 |
; |
n |
- |
1 + 3 |
|||
|
--- |
|
|
--- |
|
|||||||||
|
|
|
|
|
|
n |
|
|
|
|
4 |
|
|
|
и |
n 2 |
; |
2 1 + 6 |
и |
2 12 + 5 |
|||||||||
--- |
-- |
- |
|
|
|
-- |
|
|
|
; |
||||
|
4 |
|
3 |
|
|
|
|
3 |
|
|
|
|||
в) установите, равносильны ли неравенства: ax > a4 и x > 4;
5 |
x2 |
x |
2 |
< x; |
1 |
x |
> |
1 x – 1 |
|
|
< 5 |
и x |
------ |
|
-- |
|
|||
|
|
|
|
|
16 |
|
4 |
||
и 2x < x – 1.
УПРАЖНЕНИЯ
1. Постройте рафи фун ции (схематичес и):
а) y = –2 · 2|x|; б) y = 2|x + 3|; в) y = 2|x| + 1; ) y = –2|x| + 1; д) y = 21 – x2 ; е) y = 21 / x .
2. Решите уравнение:
а) 52x – 1 + 5x + 1 = 250; б) 6x + 6x + 1 = 2x + 2x + 1 + 2x + 2; в) 9x + 6x = 2 · 4x; ) 22x + 1 + 32x + 1 = 5 · 6x;
д) 54
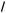 x – 14 · 52
x – 14 · 52
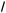 x = 275; е) (
x = 275; е) (
 4 –
4 – 
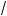 15)x + (
15)x + (
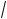 4 +
4 + 
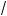 15)x = 8; ж) (
15)x = 8; ж) (
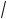 2 –
2 – 
 3)x + (
3)x + (
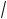 2 +
2 + 
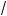 3)x = 4; з) (x – 3)3 – x2 = (x – 3)2x; и) (x + 3)x2 – 3 = (x + 3)2x; ) (x2 – x – 1)x2 – 1 = 1.
3)x = 4; з) (x – 3)3 – x2 = (x – 3)2x; и) (x + 3)x2 – 3 = (x + 3)2x; ) (x2 – x – 1)x2 – 1 = 1.
3. Решите уравнение:
а) 8x · 7x – 4 = 24 + 2x; б) 6x · 5x – 2 = 9 · 2x; в) 27 · 7x + 3 = 147x;) 625 · 9x – 2 = 15x; д) 7 · 16x = 2 · 56x; е) 125 · 8x = 50x + 1.
4. Решите уравнение:
|
|
|
|
2x – 1 |
x |
3x – 1 |
|
x |
||
а) |
|
42 – 6 |
----------------- |
------------- |
----------------- |
|
----------------- |
|||
x |
x + 1 |
= 6; б) 100 + 5 |
x |
|
2x + 1 = 5; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 1 |
|
x |
|
|
|
|
|
|
в) |
|
------------- |
– 12 |
----------------- |
= 4; ) 4 · 3x + 3 6x – 27 · 2x – 1 = 0; |
|||||
4 x |
|
2x – 1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
д) 8x + 2 · 50x = 3 · 125x; е) 24x + 6x = 10 · 3x; |
||||||||||
ж) 62x + 1 – 6x · 3x + 2 + 32x + 1 = 0. |
|
|
|
|
||||||
5. Решите уравнение: |
|
|
|
|
||||||
|
|
x + 6 |
|
x + 4 |
x + 1 |
x – 1 |
|
|||
а) |
|
------------- |
|
------------- |
------------- |
------------- |
|
|||
3x + 2 |
– 3x + 2 = 18; б) 5x – 3 – 23 · 5x |
– 3 = 250; |
||||||||
|
|
x + 1 |
|
|
x |
4x |
|
|
|
4x – 1 |
в) |
|
------------- |
|
------------- |
----------------- |
– 6 · |
----------------- |
|||
2x – 1 |
– 6 · 2x – 1 + 16 = 0; ) 32x – 1 |
32x – 1 = 243. |
||||||||
193

6. |
Решите систему уравнений: |
|
||||||
|
|
|
22x – 3y = –17, |
|
|
32x – 5y = –16, |
||
|
|
|
|
|||||
а) |
|
б) |
||||||
|
|
2x – 3y/ 2 = –1; |
3x – 5y/ 2 = –2; |
|||||
|
|
|
|
|
||||
в) |
|
|
2x + 1 |
· 3y + 2 = 2, |
) |
|
xx + y = y12, |
|
|
|
|||||||
|
|
|||||||
|
|
x – y |
= 2; |
|
yx + y |
= x3; |
||
|
|
|
|
|
||||
|
|
|
xy2 – 15 y + 56 = 1, |
|
|
642x |
+ 642y = 12, |
|
|
|
|
|
|
||||
д) |
|
е) |
||||||
|
|
y – x |
= 5; |
64x + y = 4 2 ; |
||||
|
|
|
|
|
||||
ж) |
|
3 · 2x – 2x + y + 2 = 0, |
|
|
||||
|
|
|
||||||
|
|
|
||||||
|
5 · 2x + 1 – 2x + y – 1 = 16. |
|
|
|||||
|
|
|
|
|
||||
7. |
Найдите множество значений a, при оторых система |
|||||||
уравнений:
а) 
 3 · 5y2 + 2|x| = 21 – a,
3 · 5y2 + 2|x| = 21 – a,  51 + y2 – 3|x| = 11a + 16
51 + y2 – 3|x| = 11a + 16
не имеет решений (в ответе запишите сумму целых значений a, не входящих в это множество);
б) |
|
7x + 1 |
+ 2y2 = 3a + 31, |
|
|||
|
|||
|
2 · 7x |
– 7y2 = 16a – 29 |
|
|
|
совместна (в ответе запишите наибольшее значение a из это о множества);
в) |
31 – |x| + 21 + y = 3a + 4, |
|
2 · 3–|x| + 2y = 2a |
||
|
не имеет решений (в ответе запишите целое значение a, не входящее в это множество);
) x2 + 21 – 
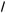 y = 5,
y = 5,
 3x2 – 22 –
3x2 – 22 – 
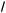 y = 2a + 9
y = 2a + 9
совместна (в ответе запишите наименьшее значение a из это о множества);
д) |
|
31 – x2 |
+ 2 y = 7a + 12, |
|
|||
|
|
|
 2 · 3–x2 – 3
2 · 3–x2 – 3
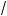 y = –4a – 5
y = –4a – 5
совместна (в ответе запишите наибольшее значение a из это о множества).
194

8. Найдите xy, если x и y — решение системы
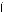 (x + 2)2 + 2 · 3|y – 2| = a – 1,
(x + 2)2 + 2 · 3|y – 2| = a – 1,  31 + |y – 2| – (x + 2)2 = 4a – 9.
31 + |y – 2| – (x + 2)2 = 4a – 9.
9. Найдите x2 – y2, если x и y — решение системы
41 + 
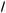 x + 3 + 2(y – 4)2 = 2a – 4,
x + 3 + 2(y – 4)2 = 2a – 4,  (y – 4)2 – 4
(y – 4)2 – 4
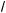 x + 3 = 7 – 2a.
x + 3 = 7 – 2a.
10. Решите неравенство: |
|
|
|
|
||||
а) |
24------------5----x- |
+ |
-------5----x-------- |
m 25; |
б) |
--7--------2---x--- + |
--5--------2---x--- |
l 12; |
|
5x – 5 |
|
5x – 30 |
|
|
2x – 1 |
2x – 7 |
|
в) 5
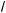 x – 2 > 51 –
x – 2 > 51 – 
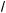 x – 2 + 4; ) 2 · 7
x – 2 + 4; ) 2 · 7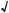 2x – 5 > 71 –
2x – 5 > 71 – 
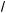 2x – 5 ;
2x – 5 ;
д) 5(x + 1)2 |
+ 625 m 5x2 + 2 + 52x + 3; |
||||||||||
е) 3 |
(x + 2)2 |
+ 1 l 3 |
x2 |
– 1 |
+ 3 · 81 |
x + 1 |
|||||
|
|
|
|
|
|
|
; |
||||
|
|
|
|
x3 – 2x + 5 |
|
|
|
|
|
x3 – x – 4 |
|
ж) |
1 |
|
------------------------------ |
|
|
|
|
|
-------------------------- |
||
|
x – 3 |
l 9; |
з) 5 |
x – 4 l 0,2; |
|||||||
-- |
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
и) (x + 3)x2 – 5 x + 6 > 1; |
|
|
|
||||||||
) 15x – 625 · 3x – |
|
3 · 5x + 25 |
|
1875 m 0. |
|||||||
11.При а их значениях k уравнение 25x – 5x + 1 – 5k – k2 = 0 имеет два решения?
12.Определите все значения параметра c, при оторых урав-
нения 4x + 2 · 2x – 3 = 0 и c · 49x + |c – 7| · 7x – 7 = 0 имеют одина-овые орни.
13. При а их значениях a уравнение 4x – 2x + 2 – 4a – a2 = 0 имеет два решения? В ответе у ажите сумму целых значений a.
Задания для повторения
14.Товарный поезд был задержан в пути на 12 мин, а затем на расстоянии 60 м наверстал потерянное время, увеличив с о- рость на 15 м/ч. Найдите первоначальную с орость поезда.
15.Пассажир поезда знает, что на данном участ е пути с о- рость это о поезда равна 40 м/ч. Ка толь о мимо о на начал проходить встречный поезд, пассажир в лючил се ундомер и заметил, что встречный поезд проходил мимо о на в течение 3 с.
195

Определите с орость встречно о поезда, если известно, что е о длина равна 75 м.
16.Решите неравенство kx + 4 > 2x + k2.
17.При а их значениях k система уравнений
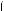 kx + 4y = 4,
kx + 4y = 4,
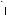 3x + y = 1
3x + y = 1
имеет решения?
О Т В Е Т Ы
2. а) x = 2; б) x = 0; в) x = 0; $) x1 = –1, x2 = 0; д) x = 1; е) x1 = –2, x2 = 2; ж) x1 = –2, x2 = 2; з) x1 = –1, x2 = 4; и) x1 = –2, x2 = –1, x3 = 3;) x1 = –1, x2 = 1, x3 = 2. 3. а) x = 4; б) x = 2; в) x = 3; $) x = 4; д) x = 1; е) x = 0,5. 4. а) x = 1; б) x = 1; в) x = 1; $) x = 2; д) x = 0; е) x = 1; ж) x1 = –1, x2 = 0. 5. а) x = 0; б) x = 4; в) x = 2; $) x = 0,75. 6. а) x = 3,
y = 4; б) x = 1, y = 2; в) x = 0, y = –2; $) x1 = 1, y1 = 1; x2 = 4, y2 = 2;
д) x |
|
= 1, y |
|
= 6; x |
|
= 2, y |
|
= 7; x |
|
= 3, y |
|
= 8; е) x |
|
1 |
, y |
|
1 |
; x |
|
1 |
, |
1 |
1 |
2 |
2 |
3 |
3 |
1 |
= -- |
1 |
= -- |
2 |
= -- |
||||||||||
|
|
|
|
|
|
|
4 |
|
6 |
|
6 |
|
y2 = 1 ; ж) x = 1, y = 2. 7. а) –9; б) a = 2; в) a = 4; $) a = 2; д) a = –1. 8. –4.
--
4
9. –7. 10. а) x < 1, 2 m x < log5 30; б) –log2 6 m x < 0, x > log2 7; в) x > 3;
$) x > 3; д) x m –
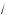 2 , 0,5 m x m
2 , 0,5 m x m 
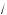 2 ; е) –1,25 m x < –1, x l 1; ж) 1 m x < 3; з) x m 2, x > 4; и) –2 < x < 2, x > 3; ) 0,5 m x m 4. 11. –5 < k < –2,5; –2,5 < k < 0. 12. 0 m c m 7, c = –7. 13. –4. 14. 60 м/ч. 15. 50 м/ч. 16. Если k = 0, то нет решений; если k < 2, то x < k + 2; если k > 2, то x > k + 2. 17. Система имеет решения при любых k.
2 ; е) –1,25 m x < –1, x l 1; ж) 1 m x < 3; з) x m 2, x > 4; и) –2 < x < 2, x > 3; ) 0,5 m x m 4. 11. –5 < k < –2,5; –2,5 < k < 0. 12. 0 m c m 7, c = –7. 13. –4. 14. 60 м/ч. 15. 50 м/ч. 16. Если k = 0, то нет решений; если k < 2, то x < k + 2; если k > 2, то x > k + 2. 17. Система имеет решения при любых k.
Решения и методичес ие у азания
К упражнению 1а
1.Фун ция y = –2 · 2|x| определена для любых значений ар$умента x. Та а 2|–x| = 2|x|, то фун ция четная, а ее $рафи симметричен относительно оси ординат.
2.При любых значениях x фун ция отрицательна, поэтому ее $рафи расположен под осью абсцисс.
3.Если x = 0, то y = –2 · 20 = –2.
4.Если x l 0, то y = –2 · 2x, а, значит, часть $рафи а, расположенная справа от оси ординат, получается симметричным отражением от
оси абсцисс части $рафи а фун ции y = 2 · 2x при x l 0 (рис. 111, а).
196
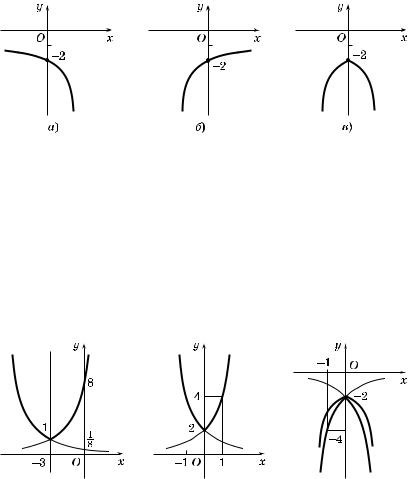
Рис. 111
–x |
= –2 · |
1 |
x |
и анало$ично получаем |
5. Если x < 0, то y = –2 · 2 |
-- |
|
||
|
|
2 |
|
часть $рафи а, расположенную слева от оси ординат (рис. 111, б).
6. Объединив построенные $рафи и, получим ис омый $рафи (рис. 111, в).
К упражнениям 1б—
См. соответственно рис. 112—114.
Рис. 112 |
Рис. 113 |
Рис. 114 |
К упражнению 1д
1. Областью определения фун ции y = 21 – x2 является вся число-
вая прямая. Та а 21 – (–x)2 = 21 – x2 , то фун ция четная, а ее $рафи симметричен относительно оси ординат.
2. Известно, что ax > 0 при любом значении x. Следовательно, $рафи фун ции цели ом расположен над осью абсцисс.
197

3. Запишем фун цию в виде
|
y = 2 |
1 – x |
2 |
= 21 · |
1 |
|
x2 |
= 2 · |
1 |
|
x2 |
|
|
|
-- |
|
-- |
. |
|||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
а) Если x º ä×, то y º 0, т. е. ось абс- |
|||||||
|
|
|
цисс является асимптотой $рафи а. |
|||||||||
|
|
|
|
|
б) Если x = ä1, то y = 1; следовательно, |
|||||||
|
|
|
точ и (1; 1) и (–1; 1) принадлежат $рафи у. |
|||||||||
|
|
|
|
|
в) При x = 0 фун ция дости$ает ма си- |
|||||||
|
|
|
мума, равно$о 2. |
|
|
|
||||||
|
|
|
|
|
$) При изменении x от –× до 0 фун ция |
|||||||
|
|
|
возрастает, а при изменении x от 0 до +× |
|||||||||
|
|
|
||||||||||
|
|
|
она убывает. |
|
|
|
|
|||||
|
|
|
|
|
4. Графи |
фун ции изображен на |
||||||
Рис. 115 |
рис. 115. |
|
|
|
|
|
|
|
||||
К упражнению 1е
1. Область определения фун ции y = 21/ x состоит из двух промежут ов: (–×; 0) и (0; +×). Следовательно, $рафи фун ции состоит из двух частей.
Рис. 116 |
2. Анализ фун ции y = 21/ x по азывает, что:
а) если x º 0 слева, то y º 0, причем y > 0; если x º 0 справа, то y º +×;
б) если x º –×, то y º 1, причем y < 1; если x º +×, то y º 1, причем y > 1;
в) значит, прямая y = 1 является асимптотой $рафи а при x º ä×.
3. Графи фун ции изображен на рис.
116.
К упражнению 2в
1. Та а x − 0, то обе части данно$о уравнения можно разделить на 4x:
9 x |
+ |
6 x |
– 2 = 0, или |
3 2x |
+ |
3 x |
– 2 = 0. |
(1) |
||||||
-- |
- |
-- |
- |
|
-- |
- |
-- |
- |
||||||
4 |
|
|
4 |
|
|
2 |
|
|
2 |
|
|
|
||
2. Положим |
3 |
- |
x |
= y (y > 0); то$да уравнение (1) запишется та : |
||||||||||
-- |
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y2 + y – 2 = 0, от уда y = 1, y = –2.
Одна о значение y = –2 не удовлетворяет условию y > 0. Следова-
тельно, |
3 |
x |
= 1, т. е. x = 0. |
-- |
- |
||
|
2 |
|
|
198

К упражнению 2е |
|
|
|
|
|
1. Упростим под оренное выражение: 4 – |
15 = (---4-----–---------15--------)--(---4-----+----------15-------) = |
||||
|
|
|
|
|
4 + 15 |
= ----------1----- |
------ , то$да ( 4 – 15)x = |
----------------1------ |
---------- |
- . |
|
4 + |
15 |
( 4 + |
15) |
x |
|
|
|
||||
|
|
|
|
||
2. Пола$ая ( 4 + 15)x = y, перепишем данное уравнение в виде |
|||||
|
1 |
+ y – 8 = 0. |
(1) |
||
|
-- |
||||
y
3. Решив уравнение (1), находим y1 = 4 – 15 , y2 = 4 + |
15 . |
|||||
Следовательно, |
|
|
|
|
||
|
|
y1 = 4 – |
15 = ( |
4 + |
15)x , |
(2) |
|
|
y2 = 4 + |
15 = ( |
4 + |
15)x . |
(3) |
4. Решим уравнение (2), для че$о преобразуем е$о левую часть, |
||||||
а в п. 1: |
|
|
|
|
|
|
4 – 15 = |
1 |
= (4 + |
15 )–1 = (4 + 15)x/ 2 , от уда x |
= –2. |
||
----- |
||||||
4 + |
|
15 |
|
|
|
|
5. На онец, из уравнения (3) следует, что 4 + 15 = ( 4 + |
15)x/ 2 , |
|||||
от уда x = 2. |
|
|
|
|
|
|
Ответ: x1 =–2, x2 = 2. |
|
|
|
|
||
К упражнению 2з
1.Выражение в левой части уравнения представляет собой фун - цию, оторая содержит переменную а в основании, та и в по азателе степени. Та ое уравнение называют по азательно-степенным.
2.При решении подобных уравнений нужно рассматривать четыре случая:
а) основание степени равно 1; б) основание степени равно 0; в) основание степени равно –1;
$) оно отлично от у азанных значений.
3.Если x – 3 = 1, т. е. x = 4, то получим 1–13 = 18 — верное равенство; поэтому x = 4 — орень уравнения.
4.Если x – 3 = 0, т. е. x = 3, то получим 0–6 = 06 — выражение, не имеющее смысла; значит, x = 3 не является орнем уравнения.
5.Если x – 3 = –1, т. е. x = 2, то получим (–1)–1 = (–1)4 — неверное равенство; следовательно, x = 2 не является орнем уравнения.
199
6. На онец, приравняв по азатели, имеем 3 – x2 = 2x, от уда x1 = –1, x2 = 3. Проверим найденные значения:
а) x1 = –1, (–4)3 – 1 = (–4)–2 — верное равенство;
б) x2 = 3 — это значение уже было рассмотрено в п. 4. Ответ: x1 = –1, x2 = 4.
К упражнению 3а
1. Упростим данное уравнение:
23x 7x |
= 24 · 22x, |
или 23x · 7x = 74 · 24 · 22x. |
(1) |
|
------------------- |
||||
7 |
4 |
|
|
|
2. Та а 22x − 0, то левую и правую части уравнения (1) можно |
||||
разделить на 22x: |
|
|
|
|
2x · 7x = 24 · 74, или |
(2 · 7)x = (2 · 7)4, т. е. x = 4. |
|
||
К упражнению 4а
1. Анализ данно$о уравнения по азывает, что, видимо, есть толь-
|
|
|
|
|
|
x |
— это возвес- |
|
о один способ освободиться от по азателя степени ------------- |
||||||||
|
|
|
|
|
|
x + 1 |
|
|
|
|
|
x + 1 |
. То$да получим равносильное |
||||
ти обе части уравнения в степень ------------- |
||||||||
|
|
|
x |
|
|
|
|
|
уравнение |
|
|
|
|
|
|
|
|
|
|
|
2x – 1 |
|
x + 1 |
|
|
|
|
|
42 – 6 |
----------------- |
= |
------------- |
. |
|
(1) |
|
|
x |
6 x |
|
||||
2. В аждом по азателе степени выделим целую часть: |
|
|||||||
2x – 1 |
1 |
x + 1 |
|
1 |
|
|
|
0. |
а) ----------------- |
= 2 – -- |
; б) ------------- = 1 + |
-- , $де x − –1 и x − |
|||||
x |
x |
x |
|
x |
|
|
|
|
3. После это$о уравнение (1) примет вид |
|
|
|
|||||
|
|
42 – 36 · 6–1/ x = 6 · 61/ x . |
|
(2) |
||||
4. Пола$ая t = 61/ x , получим вадратное уравнение t2 – 7t + 6 = 0, имеющее орни t1 = 1; t2 = 6.
5. Далее имеем 61/ x = 1, т. е. 1 = 0, — решений нет; 61/ x = 6, т. е.
--
x
1 = 1, от уда x = 1.
--
x
К упражнению 4е
1. Та а все члены уравнения содержат множитель 3x, а 3x − 0, то, разделив на 3x обе части уравнения, получим
|
24 |
|
x |
+ |
6 |
|
x |
(1) |
------ |
|
-- |
– 10 = 0, или 8x + 2x – 10 = 0. |
|||||
|
3 |
|
|
|
3 |
|
|
|
200
