Готовимся к экзамену по математике_Крамор В.С_2008 -544с

3.Решив уравнение (2), найдем y1 = –1, y2 = 0.

4.Уравнение x2 – 2x = –1 имеет орни x1 = x2 = 1.

5.Уравнение x2 – 2x = 0 имеет орни x3 = 0, x4 = 2. Ответ: x1 = x2 = 1, x3 = 0, x4 = 2.

К упражнению 7а

1.Данное уравнение содержит параметр a (переменную, оторая

врассматриваемом примере сохраняет одно и то же значение).

2.Из условия следует, что a − 0, x − a.

3.Упрощая уравнение, получим

x2 – 2ax – a2 = 0,

от уда x = a ä a2 .

Ответ: x − a, a − 0, x = a(1 ä 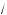2 ).

К упражнению 7б

1.Из условия следует, что x − 0, x − 1.

2.После упрощения данно)о уравнения имеем

2x2 – (2a + 1)x + a = 0.

3.Решив это уравнение, находим

=2a + 1 ± (2a – 1) . x ----------------------------------------------

4

б) если a = 0, a = 1, то x = 1 .

--

2

К упражнению 8в

1.Данное уравнение о ажется линейным, если k – 2 = 0, т. е. k = 2.

Вэтом случае уравнение имеет единственный орень.

2.Квадратное уравнение имеет единственный орень, если D = 0.

111

3. Найдем дис риминант данно)о уравнения и определим, при а-их значениях k он равен нулю:

а) D = 4k2 – 4(k – 2)(2k – 3) = –4k2 + 28k – 24; б) –4k2 + 28k – 24 = 0, k = 1 и k = 6.

Ответ: k1 = 2, k2 = 1, k3 = 6.

К упражнению 9

1.Пусть в лассе было x учащихся. По условию аждый из них получил по x – 1 от рыто .

2.Та а все)о было послано x(x – 1) от рыто , то получаем уравнение x(x – 1) = 1332, или

x2 – x – 1332 = 0, от уда x = 37.

К упражнению 10

1.Пусть x — число сторон данно)о выпу ло)о мно)оу)ольни а.

2.То)да число диа)оналей, проведенных из аждой вершины,

равно x – 3; та им образом, получаем уравнение x( x – 3) = 230, x2 – 3x –

----------------------

2

– 460 = 0, от уда x = 23.

К упражнению 11

1. Пусть было взято x л первой жид ости, то)да в ней содержится

--------------

x 85 л спирта.

100

2.Число литров второй жид ости есть 10 – x, а процентное содержание спирта в ней равно (10 – x + 66)%.

3.По условию

от уда x2 – x – 30 = 0, т. е. x = 6. Ответ: 6 и 4 л.

К упражнению 12

1. Пусть объем работы составляет A не оторых условных единиц и x — число дней, за оторое первый рабочий может выполнить все задание.

112

3. Следовательно, за 4 дня первый рабочий выполнит 4A все)о за-

---

x

дания, а второй выполнит 4 A все)о задания.

-------------

x + 5

4. Со)ласно условию, получаем уравнение

4A + 4 A = 2 A,

--- ------------- --

x x + 5 3

от уда находим x = 10. Ита , получаем ответ: 10 и 15 дней.

К упражнению 13

1.Пусть первый турист прошел расстояние от A до B за t ч, то)да второй прошел это расстояние за t – 5 ч.

2.Пусть s — расстояние от A до B. То)да с орости перво)о и второ-

от уда находим t = 10. Ответ: 10 и 5 ч.

К упражнению 17б

1. Требуется определить x31 + x32 , )де x1 и x2 — орни уравнения x2 + px + q = 0.

2.Из формул Виета следует, что x1 + x2 = –p, x1x2 = q.

3.Упростив сумму убов и выполнив подстанов у, получим

x31 + x32 = (x1 + x2)(x21 – x1x2 + x22 ) =

=(x1 + x2)((x1 + x2)2 – 3x1x2) = –p(p2 – 3q) = p(3q – p2).

Купражнению 18

1.По условию орни уравнения 3x2 + 2x – c = 0 имеют вид x1 = 2k

иx2 = 3k.

уда k = – 2 .

------

15

113

3. Найдем x1 и x2:

4. Используем дру)ую формулу Виета и найдем значение c:

К упражнению 19а

З а м е ч а н и е. Основными методами решения систем ал)ебраичес их уравнений являются метод подстанов и, метод сложения и метод введения новых переменных.

Далее на примерах мы по ажем, а используются эти методы применительно системам произвольных ал)ебраичес их уравнений.

1. Дана система уравнений

x2 + y2 + 2y = 9, 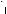3x – y – 1 = 0.

2.Из второ)о уравнения системы выразим y через x: y = 3x – 1.

3.Подставив выражение для y в первое уравнение, получим

x2 + (3x – 1)2 + 2(3x – 1) = 9.

4. Рас рыв с об и и приведя подобные члены, имеем x2 – 1 = 0. Следовательно, x1 = –1; x2 = 1. Этим значениям x соответствуют y1 = –4;

y2 = 2. Ита , x1 = –1, y1 = –4 и x2 = 1, y2 = 2 — решения системы.

К упражнению 20а

1. Дана система

x2 + xy + 2y2 = 11,

(1) 2x2 + 2xy + y2 = 10.

2. Почленное сложение уравнений системы (1) не приведет ис - лючению одной из переменных. Если же умножить все члены перво)о уравнения системы (1) на (–2), то оэффициенты при x2 в полученных уравнениях будут противоположными числами:

–2x2 – 2xy – 4y2 = –22,

(2) 2x2 + 2xy + y2 = 10.

3. Сложив почленно уравнения системы (2), получим уравнение y2 = 4, из оторо)о находим y1 = –2, y2 = 2.

114

4. Та а мы получили два значения y, то следует составить две системы уравнений, взяв одно из уравнений системы (1), и решить их. Имеем:

К упражнению 21а

З а м е ч а н и е. При решении подобных систем лучше все)о применять ис усственные приемы.

1. Дана система

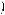x2 + y2 = 20, xy = 8.

2.Умножив второе уравнение системы на 2 и сложив результат с первым уравнением, получим (x + y)2 = 36, от уда x + y = ä6.

3.Та им образом, данная система равносильна сово упности двух систем:

4. Каждая система ле) о решается. Все)о получим четыре решения: x1 = –4, y1 = –2; x2 = –2, y2 = –4; x3 = 4, y3 = 2; x4 = 2, y4 = 4.

Эту систему можно решить дру)им способом.

1. Возведя второе уравнение системы в вадрат, получим

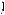x2 + y2 = 20, x2y2 = 64.

2. Пола)ая x2 = a, y2 = b, приходим системе

a + b = 20, ab = 64.

3. Решив последнюю систему, получим тот же ответ.

115

К упражнению 21б

1. Дана система

2x2 + 5xy – 18y2 = 0, xy + y2 = 12.

2.Первому уравнению системы удовлетворяют значения x = 0

иy = 0.

3.Одна о второе уравнение системы при y = 0 приводится неверному равенству: 12 = 0. Следовательно, обе части перво)о уравне-

ния можно разделить на y2, то)да получим

4. Пола)ая x = z, приходим вадратному уравнению

--

y

2z2 + 5z – 18 = 0,

орни оторо)о z = –9 и z = 2.

--

2

5. Та им образом, данная система равносильна сово упности двух систем:

6. Система а) не имеет действительных решений, система б) имеет два решения: x1 = –4, y1 = –2 и x2 = 4, y2 = 2.

К упражнению 21в

1. Дана система

x2 + 3xy = 18, 3y2 + xy = 6.

2.После анализа уравнений данной системы убеждаемся в том, что ни один из рассмотренных выше способов решения неприменим.

3.Освободимся от одночленов xy и 3xy. Умножим второе уравнение системы на (–3), то)да оэффициенты при xy в обоих уравнениях системы будут противоположными числами:

116

4. Составим новую систему из уравнения (1) и любо)о уравнения данной системы:

x2 – 9y2 = 0,

(2) 3y2 + xy = 6.

5. Система (2) равносильна сово упности двух систем:

6. Система б) не имеет действительных решений, система а) имеет два решения: x1 = –3, y1 = –1 и x2 = 3, y2 = 1.

К упражнению 21

1. Дана система

x + y = 72,

3x + 3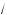y = 6.

2.Если из перво)о уравнения системы выразить x или y и сделать подстанов у во второе уравнение, то задача толь о усложнится.

3.Возведя второе уравнение системы в уб, получим

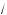x + y + 3 3xy (3x + 3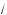y ) = 63, или 72 + 3 · 63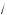xy = 63,

от уда 3xy = 8, а xy = 83 = 512. 4. Составим новую систему

xy = 512, x + y = 72,

от уда x1 = 64, y1 = 8 и x2 = 8, y2 = 64.

К упражнению 22а

1.Фун ция y = x2 + x – 2 — вадратичная; ее )рафи ом является парабола, ветви оторой направлены вверх, та а a = 1 > 0.

2.Найдем орни фун ции (если они имеются):

x2 + x – 2 = 0, x1 = –2; x2 = 1. 3. Найдем вершину параболы:

117

4.Определим точ у, в оторой )рафи фун ции пересе ает ось Oy: пола)ая x = 0, находим y = –2.

5.Используя полученные данные, изобразим схематичес и )рафи фун ции (рис. 43).

К упражнению 22б

1.Фун ция y = –x2 + 2x + 3 — вадратичная; ее )рафи ом является парабола, ветви оторой направлены вниз, та а a = –1 < 0.

2.Найдем орни фун ции: –x2 + 2x + 3 = 0, x1 = –1; x2 = 3.

3.Найдем вершину параболы: x0 = 1; y0 = 4.

4.Определим точ у, в оторой )рафи фун ции пересе ает ось Oy: при x = 0 имеем y = 3.

5.На основании полученных данных изобразим схематичес и )рафи фун ции (рис. 44).

З а м е ч а н и е. В дальнейшем при построении )рафи а фун ции

y = ax2 + bx + c мы не будем приводить столь подробных объяснений.

3. Построим часть ис омо)о )рафи а, определяемую системой (1): а) дис риминант вадратно)о трехчлена x2 – 2x + 2 отрицателен, поэтому )рафи фун ции (1) не пересе ает ось Oy и лежит выше этой

оси (та а a = 1 > 0);

118

Рис. 45

в) если x = 0, то y = 2;

)) )рафи фун ции (1) изображен на рис. 45, а.

4. Построим часть ис омо)о )рафи а, определяемую системой (2): а) дис риминант вадратно)о трехчлена x2 + 2x + 2 отрицателен, значит, )рафи фун ции (2) лежит выше оси Oy (пос оль у a = 1 > 0);

в) )рафи фун ции (2) изображен на рис. 45, б.

5. Объединив )рафи и фун ций (1) и (2), получим ис омый )рафи (рис. 45, в).

К упражнению 25а

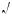1.Та а (402 )2 = 3200, а 572 = 3249, то 57 > 402 .

2.Отсюда следует, что под зна ом модуля в выражении |40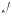2 – 57|

находится отрицательное число. Та им образом, 402 – 57 =

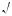=57 – 402 .

3.Обозначим ис омую разность ради алов через x:

одно из ис омых чисел.

5.Та а 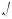57 + 40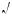2 > 57 – 40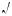2 , то ис омым является число x = –10.

119

К упражнению 26а

1. Если заданные уравнения имеют общий орень, то при не отором x выражения x2 – kx и x2 – x – 3k совпадают:

x2 – kx = x2 – x – 3k; –kx = –x – 3k; k = x .

-------------

x – 3

2. При найденном значении k = x любое из данных выражений

-------------

x – 3

должно обращаться в нуль, т. е.

x2 – x · x = 0, x2 1 – 1 = 0,

------------- -------------

x – 3 x – 3

от уда x1 = 0 или x2 = 4.

3. Возьмем любое из данных уравнений, например x2 – kx = 0. То)да:

а) если x = 0, то 0 – k · 0 = 0, т. е. k = 0; б) если x = 4, то 42 – k · 4 = 0, т. е. k = 4.

К упражнению 26б

1.Пусть x0 — общий орень данных уравнений.

2.Составим систему

x20 + kx0 + 2 = 0, x20 + 2x0 + k = 0,

из оторой следует, что (k – 2)(x0 – 1) = 0. 3. Рассмотрим два случая:

а) если k = 2, то уравнение x2 + 2x + 2 = 0 не имеет решений (таа D < 0);

б) если x0 = 1, то уравнение x2 + kx + 2 = 0 примет вид 1 + k + 2 = 0, от уда k = –3.

4. При k = –3 получаем уравнения x2 – 3x + 2 = 0 и x2 + 2x – 3 = 0,оторые имеют общий орень x = 1.

К упражнению 28

1. Масса патрона состоит из: а) массы снаряда; б) массы заряда; в) массы )ильзы.

2. Масса снаряда и )ильзы составляет 2 + 1 = 11 массы патрона.

-- -- ------

3 4 12

120