
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
2. а) Если a > 3, то a|a – 3| = a(a – 3) и, значит,
a a – 3
-------------------------------------
( a – 3) ( a + 2)
= |
a( a – 3) |
(----a----–-----3----)--(----a----+------2---)- |
= a .
-------------
a + 2
б) Если –× < a < –2 или –2 < a < 3, то a|a – 3| = –a(a – 3) и, следовательно,
a a – 3
-------------------------------------
( a – 3) ( a + 2)
= |
–a( a – 3) |
(----a----–-----3----)---(---a----+------2----) |
= – a .
-------------
a + 2
3. |
Ита , получаем ответ: |
|
||
|
------a------- |
при a > 3; – |
------a------- |
при –× < a < –2 или –2 < a < 3. |
|
a + 2 |
|
a + 2 |
|
К упражнению 10 |
|
|
||
1. |
Область определения дроби --x----2----–-----x------+-----1---- есть x Ý R. |
|||
|
|
|
|
x4 + x2 + 1 |
2. Знаменатель дроби представим в следующем виде:
x4 + x2 + 1 = (x2 + 1)2 – x2.
3.Это выражение представляет собой разность вадратов.
4.Возвращаясь данной дроби и со ратив ее, получим
--x----2----–-----x------+-----1---- = |
------x----2----–-----x-----+------1------- |
= |
--------------------x---2-----–-----x-----+------1--------------------- |
= |
-------------1-------------- |
. |
x4 + x2 + 1 |
( x2 + 1)2 – x2 |
|
( x2 + x + 1) ( x2 – x + 1) |
|
x2 + x + 1 |
|
К упражнению 12а
1.Разложим знаменатели дробей на множители: а) x2 – x – 6 = (x – 3)(x + 2);
б) 3x2 – 4x – 15 = (x – 3)(3x + 5); в) 3x2 + 11x + 10 = (x + 2)(3x + 5).
2.Найдем область определения данно"о выражения: x − 3; x − –2;
x − –5 ; x − ä1.
--
3
3. Та им образом, имеем
--------- |
---x-------------- |
– -------- |
---x-----–------1------------ |
|
: -----x----4----–-----2----x----2----+------1------ |
|
x2 – x – 6 |
3x |
2 – 4x + 5 |
|
3x2 + 11x + 10 |
||
= (---3------x---+------5----)---x----–-----(---x-----–------1---)---(--x-----+------2----) |
: |
----------(--x----2----–-----1----)--2----------- |
||||
|
( x – 3) (x + 2) ( 3x + 5) |
|
|
( x + 2)( 3x + 5) |
||
= |
-------------2----x------2--+------4----x-----+------2--------------- |
· |
-(--x------+-----2----)---(--3----x-----+------5----) = |
|||
|
( x – 3) ( x + 2) ( 3x + 5) |
|
( x2 – 1)( x2 – 1) |
|||
|
|
2( x + 1)2 |
|
|
2 |
|
= |
(---x-----–-----3------)-(--x-----–-----1----)---2---(--x-----+------1----)--2- |
= |
(---x-----–-----3----)---(--x-----–-----1----)---2- . |
|||
=
=
51
К упражнению 12д
1.Найдем область определения данно"о выражения: a − 0; b − 0;
a − b.
2.Выполнив действия в первых с об ах, получим
4----(---a-----+------b---)--2- |
– 16 = 4----a----2----–------8----ab--------+------4----b---2- |
= 4----(---a-----–-----b---)---2- . |
ab |
ab |
ab |
3. Выполнив действия во вторых с об ах, получим
(---a-----+------b---)--2----–------ab----- |
= a----2----+------2----ab--------+------b---2-----–-----ab----- |
= a----2----+------ab---------+-----b----2 . |
ab |
ab |
ab |
4. Используя равенства (1) и (2), находим
(1)
(2)
4----(---a-----–-----b----)--2- |
· a----2----+------b---2----+------ab----- |
· |
-------ab----------- |
= |
ab |
ab |
|
a3 – b3 |
|
4( a – b)2 ( a2 + b2 + ab)
-------------------------------------------------------------------
ab( a – b) ( a2 + b2 + ab)
= 4( a – b) .
---------------------
ab
К упражнению 14
Имеем
A = ----- |
----------25--------- |
---------- + |
----2----a---- |
– |
----------------a----3----+------25-------a----2--- |
-------------- · |
(---a-----–-----5----)--2----+------15---------a |
= |
|||
a2 + 5a + 25 |
a – 5 |
|
( a – 5) ( a2 + 5a + 25) |
a – 5 |
|
|
|
||||
= 25---------(-a-----–------5---)----+------2----a----(--a----2----+------5----a----+---------25-----)---–-----a----3----–-----25--------a----2 |
· a----2----–------10--------a----+------25--------+------15-------a-- |
= |
|
||||||||
|
|
( a – 5) ( a2 + 5a + 25) |
|
|
a – 5 |
|
|
|
|||
= |
25--------a-----–-------125----------+------2----a---3-----+-----10--------a-----2---+-----50--------a-----–-----a----3----–-----25-------a----2- · a----2-----+-----5----a-----+------25----- |
= |
|
|
|||||||
|
|
( a – 5) ( a2 + 5a + 25) |
|
|
a – 5 |
|
|
|
|||
|
|
= a----3----–------15-------a----2----+-----75--------a-----–-----125--------- |
· a----2----+------5----a-----+------25----- |
= |
|
|
|
||||
|
|
( a – 5) ( a2 + 5a + 25) |
|
a – 5 |
|
|
|
|
|||
|
|
( |
)3( 2 |
|
) |
|
|
|
|
|
|
|
|
a – 5 |
a |
+ 5a + 25 |
|
|
|
|
|
|
|
|
= (----a----–-----5----)--(---a----2----+-----5----a-----+------25-------)---(--a-----–------5----) |
= a |
– 5, "де a − 5. |
|
|
|
|||||
К упражнению 15
1.Пусть 5x — первое число; то"да 3x — второе число, 20x — третье, 20x · 0,15 = 3x — четвертое.
2.По условию
5x + 20x + 3x – 3x = 375,
от уда x = 15.
3. Значит, ис омые числа та овы: 5x = 5 · 15 = 75; 3x = 3 · 15 = 45; 20x = 20 · 15 = 300, 3x = 3 · 15 = 45.
К упражнению 16
1. Пусть a — цифра десят ов, а b — цифра единиц исходно"о числа. То"да это число равно 10a + b, а сумма е"о цифр равна a + b.
52
2. |
Со"ласно условию, имеем |
|
|
|
10--------a-----+------b- = 8 + |
------1------- . |
(1) |
|
a + b |
a + b |
|
3. |
Из равенства (1) следует, что |
|
|
|
2a = 7b + 1, или a = 7----b-----+------1- . |
(2) |
|
|
|
2 |
|
4.Та а a и b— натуральные числа, меньшие 10, то из равенства (2) перебором устанавливаем, что наименьшему значению b = 1 соответствует значение a = 4.
5.Запишем частное от деления исходно"о числа на произведение е"о цифр:
10--------a-----+------b- . |
(3) |
ab |
|
6. Подставив в выражение (3) найденные значения a = 4, b = 1, получим
10--------a-----+------b- |
= 10------------4-----+------1- |
= 41------ . |
ab |
4 1 |
4 |
7. Ита , ис омый остато равен остат у от деления 41 на 4, т. е. он равен 1.
К упражнению 17
З а м е ч а н и е. Если p% неизвестно"о числа x равны b, то само неизвестное число получается делением b на 0,01p.
Та им образом, если p%(x) = b, то
x = |
--------b-------- |
, или x = 100-----------b-- . |
|
0, 01p |
p |
1.Пусть размер в лада равен x (р.); то"да е"о 12% составляют 2700 р., т. е. 12%(x) = 2700, или 0,12x = 2700.
2.Отсюда
x = 2700 = 22 500 р.
-------------
0,12
К упражнению 18
1.В 800 " моло а содержится 5% жира, т. е. 0,05 · 800 = 40 "
жира.
2.Этот же жир сохраняется и в сметане.
3.Пусть из 800 " моло а можно получить x " сметаны, то"да
вней имеется 0,25x " жира.
4.Та им образом, 0,25x = 40, от уда x = 160 ( ").
53

Т е м а 5
À
Понятие об иррациональном числе. Множество действительных чисел.
Арифметические действия с действительными числами. Корень k/й степени из действительного числа.
Преобразования арифметических корней. Степени с целым и дробным показателями.
Примеры применения тождеств сокращенного умножения к действиям над степенями
Теоретичес ие сведения
1. Понятие об иррациональном числе
1°. При измерении отрез ов, несоизмеримых с единицей длины, получается число, оторое выражается бес онечной непериодичес ой десятичной дробью. Та ие числа называют иррациональными; например: 0,131331333125... . Известное в математи е число π, число e (основание натуральных ло а- рифмов) та же являются числами иррациональными.
2°. Дру ой пример, приводящий понятию иррационально-о числа, дает следующая теорема: не существует рационально-о числа, вадрат оторо о равен двум. Иными словами, решение уравнения x2 – 2 = 0 невозможно на множестве рациональных чисел. Корнями та о о уравнения являются иррациональные
числа 
 2 и –
2 и –
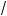 2 .
2 .
3°. Любое рациональное число вида m ( де n − 0) можно
----
n
представить в виде онечной или бес онечной периодичес ой десятичной дроби.
2. Множество действительных чисел
1°. Объединение множеств рациональных и иррациональных чисел образует множество действительных (или вещественных) чисел. Это множество принято обозначать через R.
54
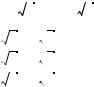
2°. Между множеством R и множеством точе оординатной прямой существует взаимно однозначное соответствие, т. е.аждому действительному числу соответствует единственная точ-а оординатной прямой и наоборот, аждой точ е оординатной прямой соответствует единственное действительное число.
Учитывая это взаимно однозначное соответствие, часто множество R действительных чисел и множество точе оординатной прямой объединяют общим термином — «числовая прямая».
3°. Действительные числа сравнивают по величине со ласно правилу сравнения рациональных чисел (см. тему 3, п. 6). Например, –0,17... < –0,15; 3,1... > –5,6... .
4°. Для числовых промежут ов вводят следующие обозначения:
[a; b] = {x Ý R | a m x m b} — зам н тый промеж то (или
отрезо ) с началом a и онцом b;
(a; b) = {x Ý R | a < x < b} — от рытый промеж то (или интервал);
(a; b] = {x Ý R | a < x m b}; [a; b) = {x Ý R | a m x < b} — пол - от рытые промеж т и;
[a; +×) = {x Ý R | x l a}; (–×; b] = {x Ý R | x m b} — л чи; (a; +×) = {x Ý R | x > a}; (–×; b) = {x Ý R | x < b} — от ры-
тые л чи;
(–×; +×) = R — числовая прямая.
3. Арифметические действия с действительными числами
1°. Пусть даны действительные числа a и b. Обозначим через ak–, ak+, bk–, bk+ приближенные значения этих чисел с недостат ом
1 |
, т. е. a– < a < a+ и b– < b < b+. |
||
и с избыт ом с точностью до --------- |
|||
10k |
k |
k k |
k |
2°. С ммой действительных чисел a и b называют та ое действительное число p, оторое при любом целом неотрица-
тельном k удовлетворяет неравенству a– + b– < p < a+ |
+ b+. |
||||||||
|
|
|
|
|
|
k |
k |
k |
k |
Например, для чисел a = |
2 и b = 3 имеем |
|
|||||||
1,4 |
+ 1,7 |
< |
2 |
+ |
3 |
< 1,5 |
|
+ 1,8; |
|
1,41 |
+ 1,73 |
< |
2 |
+ |
3 |
< 1,42 |
|
+ 1,74; |
|
1,414 |
+ 1,732 |
< |
2 |
+ |
3 |
< 1,415 |
+ 1,733; |
|
|
............................................................... |
|
||||||||
55

3°. Произведением действительных чисел a и b называют та ое действительное число q, оторое при любом целом неот-
рицательном k удовлетворяет неравенству ak–bk– < q < ak+bk+. Например, для чисел a = 
 2 и b =
2 и b = 
 3 имеем
3 имеем
1,4 |
· 1,7 |
< |
2 |
· |
3 |
< 1,5 |
· 1,8; |
1,41 |
· 1,73 |
< |
2 |
· |
3 |
< 1,42 |
· 1,74; |
1,414 |
· 1,732 |
< |
2 |
· |
3 |
< 1,415 |
· 1,733; |
.............................................................
4°. Известные для рациональных чисел за оны арифметиче- с их действий (переместительный, сочетательный, распределительный) сохраняются и для любых действительных чисел.
4. Корень k/й степени из действительного числа
1°. Корнем k-й степени ( де k Ý N и k − 1) из действительно о числа a называют действительное число x, k-я степень о- торо о равна a.
2°. Корень k-й степени из числа a обозначают символом k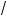 a . Со ласно определению, (k
a . Со ласно определению, (k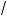 a )k = a.
a )k = a.
3°. Нахождение орня k-й степени из числа a называют извлечением орня. Число k называют по азателем орня, число a — под оренным выражением.
4°. Заметим, что 2n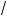 a , де n Ý N и a < 0, не существует. На-
a , де n Ý N и a < 0, не существует. На-
пример, выражения 
 –4 ; 4
–4 ; 4 –16 не имеют смысла.
–16 не имеют смысла.
5°. Чтобы устранить двузначность орня k-й степени из числа a, вводят понятие арифметичес о о орня. Арифметичес иморнем k-й степени из числа a (a l 0) называют неотрицательное число b, k-я степень оторо о равна a, де k > 1 — натуральное число.
Например: а) k ak = |a|; б)
ak = |a|; б) 
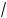 x2 + 2x + 1 +
x2 + 2x + 1 + 
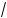 x2 – 2x + 1 = = |x + 1| + |x – 1|; в) 4 (–3)4 = |–3| = 3; )
x2 – 2x + 1 = = |x + 1| + |x – 1|; в) 4 (–3)4 = |–3| = 3; ) 
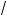 9 = 3 (но не ä3).
9 = 3 (но не ä3).
З а м е ч а н и е. В ш ольном урсе рассматривается толь о ариф-
метичес ое значение орня, т. е. k a имеет смысл лишь при a l 0 и принимает толь о неотрицательные значения.
a имеет смысл лишь при a l 0 и принимает толь о неотрицательные значения.
56

5. Преобразования арифметических корней
1°. Корень k-й степени из произведения неотрицательных чисел равен произведению орней той же степени из сомножителей:
k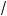 ab = k
ab = k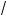 a · k
a · k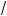 b
b
(правило извлечения орня из произведения). 2°. Если a l 0, b > 0, то
a |
k a |
k -- |
= ------- |
b |
k b |
(правило извлечения орня из дроби). 3°. Если a l 0, k, c Ý N, k, c > 1, то
k c
c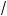 a = kc
a = kc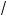 a
a
(правило извлечения орня из орня). 4°. Если a l 0, то
(k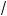 a )m = k
a )m = k am
am
(правило возведения орня в степень). 5°. Если a l 0, то
k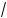 am = nk
am = nk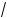 anm ( де m, n Ý N),
anm ( де m, n Ý N),
т. е. по азатель орня и по азатель под оренно о выражения можно умножить на одно и то же число.
6°. Если a1 > a2 > 0, то k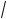 a1 > k
a1 > k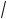 a2 > 0, т. е. большему поло-
a2 > 0, т. е. большему поло-
жительному под оренному выражению соответствует и большее значение орня.
7°. Все у азанные выше формулы часто применяются в обратном поряд е (т. е. справа налево). Например:
а) 
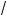 3 ·
3 · 
 2 =
2 = 
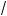 3 2 =
3 2 = 
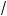 6 (правило умножения орней);
6 (правило умножения орней);
10 |
= |
10 |
= |
2 (правило деления орней); |
б) ---------- |
------ |
|||
5 |
|
5 |
|
|
в) 6 5 |
= 3 |
5 . |
|
|
57

8°. Правило вынесения множителя из-под зна а орня:
k ak b = |a|k
ak b = |a|k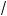 b .
b .
Например, 
 27a2 = 3 · |a|
27a2 = 3 · |a|
 3 .
3 .
9°. Обратная задача — внесение множителя под зна орня. Например,

 3b2 , если b l 0, b
3b2 , если b l 0, b 3 =
3 = 

– 3b2 , если b < 0.
3b2 , если b < 0.
10°. Уничтожение иррациональности в знаменателе дроби. Если знаменатель дроби содержит иррациональное выражение (т. е. выражение, в отором имеются действия с орнями), то целесообразно избавиться от последне о.
Рассмотрим не оторые типичные случаи.
а) ---A----- = -----A----n------a---n----–----1----- = ---A--n-----a----n----–----1- = |
A-----n-----a----n----–----1- |
, та а a > 0. |
|||||||||||||
|
n a n a n an – 1 |
|
|
n an |
|
|
|
a |
|
|
|
|
|||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
5 |
= |
5 3 32 |
= |
5 |
3 9 |
= |
53 |
9 |
. |
|||
|
|
|
3------3- |
------- |
------------- |
---- |
------- |
----- |
3---- |
-- |
|||||
|
|
|
|
3 3 3 32 |
|
3 33 |
|
|
|
|
|||||
б) A |
= |
A( |
|
− |
b) |
= |
A( |
− |
b) . |
||||||
--a---- |
-+------ |
---a-----+------- |
|||||||||||||
|
a ± b |
( |
a ± |
b)( |
− |
|
|
|
a – b |
|
|
|
|||
|
a + b) |
|
|
|
|
|
|
|
|||||||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
--- |
-------3----------- |
= ------- |
-----3-----(------5-----+----------2----)------------ |
|
= |
3----(-------5-------+--------2----) = 5 + 2 . |
|||||||||
|
5 – 2 |
( 5 – 2)( 5 + 2) |
|
|
5 – 2 |
|
|
||||||||
в) |
A |
|
= |
|
|
|
A(( a + b) + c) |
|
|
и т. д. |
|||||
----------------------- |
------------ |
------ |
------ |
------- |
------------------ |
----- |
------- |
--------- |
---------- |
---- |
---- |
----- |
|||
|
a + b – c |
|
(( a + b) – c)(( a + b) + c) |
||||||||||||
11°. Применение тождеств со ращенно о умножения действиям с арифметичес ими орнями:
1)(
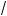 a –
a – 
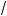 b )(
b )(
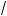 a +
a + 
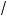 b ) = a – b;
b ) = a – b;
2)(3 a å 3
a å 3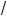 b )(3
b )(3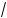 a2 ä 3
a2 ä 3 ab + 3
ab + 3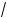 b2 ) = a å b;
b2 ) = a å b;
3)a
 a ä b
a ä b
 b = (
b = (
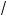 a )3 ä (
a )3 ä (
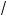 b )3 = (
b )3 = (
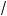 a ä
a ä 
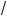 b )(a å
b )(a å 
 ab + b).
ab + b).
58

6. Степени с целым и дробным показателями
Рассмотрим степень ap, де p Ý Z.
1°. Если p = 0, то по определению a0 = 1 (при a − 0). Например, 50 = 1.
2°. Если p < 0, то по определению ap = |
1 |
(при a − 0). На- |
||||||||||
-------- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a–p |
|
пример, 2 |
–1 |
1 |
–2 |
1 |
; (–3) |
–1 |
|
1 |
; |
2 |
–1 |
3 |
|
=-- ; 2 |
|
= ----- |
|
= –-- |
-- |
|
= -- . |
||||
|
|
2 |
|
22 |
|
|
|
3 |
|
3 |
2 |
|
3°. Рассмотрим степень ap/q, де |
p |
— рациональное число. |
||||||||||
-- |
||||||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
Выражение ap/q имеет в общем виде смысл толь о при a > 0. Если a > 0, p Ý Z, q Ý N, то по определению ap/q = q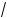 ap . На-
ap . На-
пример, 22/3 = 3 22 . Выражение (–8)1/2 или (–8)3/4 смысла не имеет.
22 . Выражение (–8)1/2 или (–8)3/4 смысла не имеет.
4°. Степень с рациональным по азателем обладает теми же свойствами, что и степень с натуральным по азателем, а именно, если a > 0 и n Ý Q, m Ý Q, то:
а) am · an = am + n; б) am : an = am – n; в) (an)m = anm;
) (ab...k) |
n |
n |
· b |
n |
... k |
n |
; |
д) |
a n |
an |
|
|
= a |
|
|
-- |
|
= ----- . |
|||||
|
|
|
|
|
|
|
|
|
b |
bn |
|
7. Примеры применения тождеств сокращенного умножения
кдействиям над степенями
1.(a1/2 – b1/2)(a1/2 + b1/2) = a – b.
2.(a1/3 ä b1/3)(a2/3 å a1/3b1/3 + b2/3) = a ä b.
3.a3/2 å b3/2 = (a1/2)3 å (b1/2)3 = (a1/2 å b1/2)(a ä a1/2b1/2 + b).
4.a2/3 – b2/3 = (a1/3)2 – (b1/3)2 = (a1/3 – b1/3)(a1/3 + b1/3).
|
|
2x–1/ 3 |
|
x2/ 3 |
5. |
x-------2-/-3----–------3----x---–1-------/-3- |
|
– x-----5---/-3----–------x----2---/--3 |
|
|
|
x2/ 3 |
|
x + 1 |
|
–---x--2---/-3---(---x-----–-----1----) |
– |
(----x----–-----1----)---(---x----–-----3----) |
|
|
= |
2----(---x-----–-----1-----)---–-----(--x-----–------3---)----–-----(---x-----+------1----) |
||
|
|
(x – 1)(x – 3) |
||
– |
x + 1 |
= |
2x–1/ 3 |
||
x----2-----–------4---x-----+-----3-- |
x-----–1------/-3---(---x-----–-----3----) |
||||
= |
------2------- |
– |
------1------- |
– |
------------x-----+------1------------- |
|
x – 3 |
|
x – 1 |
|
(x – 1)(x – 3) |
= |
2----x------–-----2-----–------x----+------3------–----x-----–-----1-- = 0. |
||||
|
(x – 1)(x – 3) |
|
|||
–
=
59

6. x---------x-----+-----y--------y-- : (x – y) + --- |
---------y----- |
---- = |
|
|
|
|
|
x + y |
|
x + |
y |
|
|
|
|
= (-------x-----+----------y----)--(---x-----–------------xy------+------y----) + |
------------y--------- = |
|
|
|
|
||
( x + y)(x – y) |
|
x + y |
|
|
|
|
|
= x------–---------xy---------+------y- + ----- |
-------y-------- |
- = --x----–---------xy---------+------y----+----------y----(-------x-----–---------y----) |
= |
|
|||
x – y |
x + |
y |
x – y |
|
|
|
|
= x------–---------xy---------+------y----+--------------xy-----–-----y-- |
= ------ |
x------ . |
|
|
|
|
|
x – y |
|
x – y |
|
|
|
|
|
7. ((5 5 )–2/3 – 81–0,25) · ((5 |
5 )–2/3 + 81–0,25) = (5 |
5 )–4/3 – |
|||||
– 81–0,5 = (53/2)–4/3 – (92)–0,5 = 5–2 – 9–1 = |
--1---- |
– 1-- |
= – |
--16------- . |
|||
|
|
|
|
25 |
9 |
|
225 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Ка ие числа называют иррациональными?
2.Существует ли рациональное число, выражающее длину диа"онали вадрата со стороной, равной 1?
3.Может ли быть выражено рациональным числом отношение длины о ружности диаметру?
4.В чем за лючается взаимно однозначное соответствие между множеством действительных чисел и множеством точе оординатной прямой?
5.Изобразите на оординатной прямой точ и, оторым соответствуют иррациональные чис-
ла 
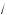 2 ,
2 , 
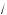 3 .
3 .
6.Может ли бес онечная десятичная дробь быть числом рациональным, иррациональным?
7.Ка ие числа называют действительными?
8.С помощью зна а ô запишите соответствие между мно-
жествами N, Z0, Z, Q и R.
9. Сравните числа 0,333...
и1 .
--
3
10.Запишите в виде бес о-
15 |
3 |
; |
нечной десятичной дроби: ------ |
; -- |
|
8 |
7 |
|
5; 2,7. |
|
|
11.Дайте определение орня k-й степени из действительно"о числа a.
12.С оль о значений имеет
орень k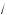 a , если: а) k = 2n; n Ý N; a > 0; б) k = 2n – 1; n Ý N; a > 0; в) k Ý N, k − 1; a < 0; a = 0?
a , если: а) k = 2n; n Ý N; a > 0; б) k = 2n – 1; n Ý N; a > 0; в) k Ý N, k − 1; a < 0; a = 0?
13. Ка ой орень называют арифметичес им? Верно ли, что

 9 = ä3?
9 = ä3?
14. Сформулируйте: а) правила извлечения орня из произведения и умножения оней; б) правила извлечения орня из дроби и деления орней; в) правило извлечения орня из орня и основное свойство орня; ") правило сравнения орней с одина овыми по азателями.
60
