Готовимся к экзамену по математике_Крамор В.С_2008 -544с

Та им образом, модуль числа есть расстояние от начала отсчета до точ и, оторой соответствует это число.

6. Сравнение рациональных чисел

Из установленно о на оординатной прямой соответствия следует, что то число больше, оторое расположено правее. Отсюда следует, что: а) вся ое положительное число больше нуля и больше отрицательно о числа; б) вся ое отрицательное число меньше нуля; в) из двух отрицательных чисел больше то, модуль оторо о меньше. Например, –3,8 > –5,1, та а |–3,8| < |–5,1|.

7. Сложение и вычитание рациональных чисел

1°. Сумма двух чисел с одина овыми зна ами равна числу то о же зна а, модуль суммы равен сумме модулей сла аемых. Например,

(–6) + (–5,3) = –(6 + 5,3) = –11,3.

2°. Сумма двух чисел с разными зна ами равна числу, модуль оторо о получается вычитанием из больше о модуля меньше о, а зна суммы совпадает со зна ом сла аемо о, имеюще о больший модуль. Например,

(+4) + (–10) = –(10 – 4) = –6.

3°. Сумма противоположных чисел равна нулю. Например,

(+6) + (–6) = 0.

4°. Чтобы вычесть из числа a число b, достаточно уменьшаемому прибавить число, противоположное вычитаемому. Например,

a – b = a + (–b); –5 – (+3) = –5 + (–3) = –8.

8. Умножение и деление рациональных чисел

1°. Произведение двух чисел одно о зна а есть число положительное. Например,

(–6) · (–2,3) = 13,8.

31

2°. Произведение двух чисел с разными зна ами есть число отрицательное. Например,

(+6) · (–2,3) = –13,8.

3°. Анало ично производится деление. Например:

а) (–18) : (–9) = 2; б) (+24) : (–3) = –8.

9. Возведение рациональных чисел в степень с натуральным показателем

1°. Степенью числа a с по азателем k, де a Ý Q, k Ý N, называют произведение k множителей, аждый из оторых равен a:

ak = a · a ... a.

k раз

Число a называют основанием степени, а число k — по а- зателем степени.

2°. Четная степень отрицательно о числа есть число поло-

жительное; например, (–3)24 > 0.

Нечетная степень отрицательно о числа есть число отрица-

тельное; например, (–0,75)17 < 0.

Любая степень положительно о числа есть число положительное; например, 12k > 0.

3°. При возведении нуля в любую натуральную степень k получается нуль, т. е. 0k = 0.

4°. При возведении единицы в любую натуральную степень k получается единица, т. е. 1k = 1.

КОНТРОЛЬНЫЕ ВОПРОСЫ

32

УПРАЖНЕНИЯ

1.Найдите дополнение множества чисел, ратных 4, до множества чисел, ратных 2.

2.Запишите без зна а модуля выражение:

а) |x – 2| + 3x; б) |x + 2| – 3x; в) |x – 2| – 3x;) –3|x – 2| + 4x.

3. Освободитесь от зна ов модулей в выражении: а) 2|3 – x| – 3|3x + 7| – 7x; б) 2|x – 3| – 3|3x + 7| + 7x; в) |x + 2| – x; ) |x – |x|| + 2x.

а) 0,5(|a + x| – |a – x|) при a = –2, x = –6;

б) |a – x| – |y + k| при a = –5, x = 4, y = 1, k = –3.

6. Где на оординатной прямой расположены числа, дляоторых:

а) |x| < 1; б) |x| > 3; в) –2 < |x| < 4?

7. Пусть x — натуральное число. Ка ому числовому множеству принадлежит число:

а) x + 2; б) 2x; в) x(x + 2); ) (x3 + 1) : (x + 1); д) (x3 + 1) : (x2 + 1)?

33

Задания для повторения

8. Верно ли утверждение:

а) если натуральное число делится нацело на 6, то оно делится на 3;

б) если сумма двух чисел — четное число, то аждое сла-аемое четно;

в) если произведение двух чисел равно нулю, то аждый сомножитель равен нулю;

) если уб не оторо о числа делится нацело на 8, то это число четное?

9.До ажите, что сумма трех последовательных натуральных чисел делится нацело на 3, а их произведение делится на 6.

10.Рабочие в теплице собрали 42 свежих рибов, содержащих по массе 95% воды. Ко да рибы подсушили, их масса

стала равной 3 . Ка ов процент содержания воды по массе в сухих рибах?

О Т В Е Т Ы

1. 4k + 2, k Ý Z. 2. а) 4x – 2, если x l 2; 2x + 2, если x < 2; б) 2 – 2x, если x l –2; –4x – 2, если x < –2; в) –2x –2, если x l 2; 2 – 4x, если x < 2;

если – 7 m x < 3; –27, если x l 3; в) 2, если x l –2; –2 – 2x, если x < –2;

--

3

") 2x, если x l 0; 0, если x < 0. 4. а) x l 0; б) x l 0; в) x m 0; ") x m 0. 5. а) 2; б) 7. 6. а) –1 < x < 1; б) x < –3 и x > 3; в) –4 < x < 4. 7. а) N; б) N; в) N; ") N; д) Q. 8. а) Да; б) нет; в) нет; ") да. 10. 30%.

Решения и методичес ие у азания

К упражнению 1

1.Множество чисел, ратных 4, — это числа вида 4k, "де k Ý Z. Очевидно, эти числа ратны та же и 2.

2.Из чисел вида 4k + 1, 4k + 2, 4k + 3, не ратных 4, ратны 2 толь о числа вида 4k + 2.

3.Та им образом, ис омым является множество чисел вида 4k + 2, "де k Ý Z.

34

К упражнению 2а

1.В данном выражении |x – 2| + 3x первое сла"аемое |x – 2| связано

смодулем, а второе 3x не связано.

2.Используя определение модуля, получаем

Ита ,

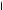4x – 2, если x l 2; |x – 2| + 3x = 2x + 2, если x < 2.

К упражнению 3а

1.Дано выражение 2|3 – x| – 3|3x + 7| – 7x.

2.Определим точ и, в оторых выражения, находящиеся под зна-ом модуля, равны нулю. Из уравнений 3 – x = 0 и 3x + 7 = 0 следует,

4. Рассмотрим данное выражение на аждом промежут е и упростим:

К упражнению 9

1.Три последовательных натуральных числа мо"ут быть записаны в следующем виде: k; k + 1; k + 2.

2.Их сумма k + k + 1 + k + 2 = 3k + 3 делится на 3, та а аждое сла"аемое делится на 3.

35

3.Произведение этих же чисел равно k(k + 1)(k + 2). Одно из записанных чисел обязательно делится на 2, а дру"ое — на 3.

4.Значит, произведение будет делиться на 6.

К упражнению 10

1. Найдем оличество воды, оторое содержится в 42 " свежих "рибов:

-----------------

42 95 = 39,9 ( ").

100

2.Значит, из 42 " свежих "рибов получили 42 – 39,9 = 2,1 " сухих "рибов.

3.Найдем оличество воды в подсушенных "рибах: 3 – 2,1 = 0,9 ".

4.Ис омое процентное отношение составляет

--------

0,9 · 100% = 30%.

3

36

Т е м а 4

À

Свойства степени с натуральным показателем. Числовые выражения. Выражения с переменными. Тождественно равные выражения. Одночлены. Многочлены. Преобразование суммы и разности многочленов. Умножение многочлена на одночлен и многочлена

на многочлен. Разложение многочлена на множители способом вынесения общего множителя за скобки.

Разложение многочлена на множители способом группировки. Тождества сокращенного умножения.

Выделение квадрата двучлена из квадратного трехчлена. Примеры использования различных способов разложения на множители. Дробь

Теоретичес ие сведения

1. Свойства степени с натуральным показателем

1°. При умножении степеней с одина овыми основаниями по азатели с ладываются, а основание остается прежним:

ak · ac = ak + c; k, c Ý N.

Например, a2 · a3 = a2 + 3 = a5.

2°. При делении степеней с одина овыми основаниями по-азатели степеней вычитаются, а основание остается прежним:

ak : ac = ak – c; k, c Ý N.

Например, a5 : a3 = a5 – 3 = a2.

3°. При возведении степени в степень по азатели степеней перемножаются, а основание остается прежним:

(ak)c = akc; k, c Ý N.

Например, (a4)3 = a12.

4°. Степень произведения равна произведению степеней

множителей:

(abc)k = akbkck; k Ý N.

Например, (abc)2 = a2b2c2.

37

5°. Степень частно о равна частному степеней делимо о и делителя:

2. Числовые выражения

1°. С помощью чисел, зна ов действий и с обо можно сос-

а не все у азанные действия можно выполнить (деление на нуль невозможно).

3. Выражения с переменными

1°. Примерами выражений с переменными являются выра-

жения 5 + a , x2 + y2 – 1 и т. д. Значение выражения, содержа-

--

3

ще о переменную, зависит от значения переменной.

2°. При не оторых значениях переменных выражение с переменными может не иметь смысла. Например, выражение

3°. Множество значений переменных, при оторых выражение с переменными имеет смысл, называют областью определения это о выражения.

38

4. Тождественно равные выражения

1°. Два выражения называют тождественно равными, если при всех значениях входящих в них переменных, принадлежащих общей области определения, соответственные значения этих выражений равны. Тождественное равенство обозначается символами = или Þ.

2°. Равенства, в оторых левая и правая части — тождественно равные выражения, называют тождествами. Например,

(a – x)2 = a2 – 2ax + x2; a3 – 8 = a2 + 2a + 4 при a − 2 — тождества.

---------------

a – 2

5. Одночлены

1°. Выражение, представляющее собой произведение чисел, переменных и степеней переменных, называют одночленом. Например, 3ax4, –2b3, 0,5c3(–3b2) — одночлены. Выражения

x + 1, a2 + b4, 3y3 не являются одночленами, та а представ-

---------

x

ляют сумму или частное переменных и чисел.

2°. Стандартным видом одночлена называют произведение, составленное из числово о множителя ( оэффициента) и бу - венно о выражения, в отором аждая из переменных взята в на-

3°. Степенью одночлена стандартно о вида называют сумму по азателей степеней переменных. Например, 8x4y2 — одночлен шестой степени, степень одночлена 3x равна единице, а степень одночлена 5 равна нулю.

4°. Одночлены, отличающиеся толь о числовым оэффициентом или равные между собой, называют подобными.

6. Многочлены

1°. Ал ебраичес ую сумму одночленов называют мно о- членом. Например, 2a2 – 3ax5 – 3 есть мно очлен. Выражение

y – xy2 + x + 3 не является мно очленом, та а не все е о сла-

--

x

аемые — одночлены.

39

2°. Если в мно очлене все одночлены записаны в стандартном виде и приведены подобные члены, то полученный мно о- член называют мно очленом стандартно о вида. Например, 2x2a3 + 1,8xa4 – 3a + 7 — мно очлен стандартно о вида.

3°. Степенью мно очлена стандартно о вида называют наибольшую степень одночлена, входяще о в этот мно очлен. Например, 1 + 2x2 – 5x2y3 — мно очлен пятой степени.

7. Преобразование суммы и разности многочленов

1°. Для то о чтобы преобразовать сумму или разность мно о- членов в мно очлен стандартно о вида, надо: а) рас рыть с об-и; б) привести подобные члены (сла аемые).

2°. Рас рытие с обо . Если перед с об ами стоит зна «плюс», то, рас рывая с об и, следует сохранить зна аждо-о сла аемо о суммы, за люченной в с об и.

Если перед с об ами стоит зна «минус», то, рас рывая с об-и, надо зна и сла аемых поменять на противоположные.

3°. Приведение подобных членов (сла аемых). Чтобы привести подобные сла аемые, достаточно сложить их оэффициенты (по правилу сложения положительных и отрицательных чисел) и полученное число умножить на бу венное выражение.

Например,

(5x2 – 4x + 3) – (3x2 – x + 2) =

=5x2 – 4x + 3 – 3x2 + x – 2 = 2x2 – 3x + 1.

За м е ч а н и е. Если мно"очлен следует за лючить в с об и, то это делается по правилу, анало"ичному рас рытию с обо . Например,

17a4 – 8a3y – 6a2y2 – ay3 = (17a4 – 8a3y) – (6a2y2 + ay3).

8. Умножение многочлена на одночлен и многочлена на многочлен

1°. Чтобы умножить мно очлен на одночлен, достаточноаждый член мно очлена умножить на одночлен и полученные произведения сложить.

2°. Деление мно очлена на одночлен производится по анало ичному правилу.

40