Готовимся к экзамену по математике_Крамор В.С_2008 -544с

ные три положительны, т. е. P(x) < 0; далее, в интервале (–2; 0) имеем P(x) > 0, а в интервале (–3; –2) имеем P(x) < 0, на онец, в интервале (–×; –3) все четыре сомножителя отрицательны,

т.е. P(x) > 0.

Врезультате получаем ответ: (–×; –3) (–2; 0) (1; +×). 2. Решить неравенство

(x – 2)3(x + 1)(x – 1)2(x2 + 2x + 5) < 0.

Р е ш е н и е. Трехчлен x2 + 2x + 5 при всех x Ý R принимает положительные значения (та а D = 22 – 4 · 5 < 0). Поэтому данное неравенство равносильно неравенству P(x) = (x + 1) × × (x – 1)2(x – 2)3 < 0 (распола аем множители в поряд е возрастания орней). Та им образом, получаем следующие интервалы зна опостоянства: (–×; –1), (–1; 1), (1; 2) и (2; +×) (рис. 57).

Рис. 57

В интервале (2; +×) все три сомножителя положительны и, значит, P(x) > 0; в интервале (1; 2) сомножитель (x – 2)3 становится отрицательным, а остальные два положительны, т. е. P(x) < 0; в интервале (–1; 1) зна второ о сомножителя (x – 1)2 не меняется, т. е. по-прежнему P(x) < 0; на онец, в интервале (–×; –1) два сомножителя отрицательны, а один положителен, т. е. P(x) > 0. Ита , получаем ответ: (–1; 1) (1; 2).

3. Решить неравенство (x – 3)2(x – 2)x > 0.

-------------------------------------------

(x + 1)4(x + 5)

Ре ш е н и е. Отметим на числовой прямой точ и x = –5, x = –1, x = 0, x = 2, x = 3 и исследуем изменение зна ов левой части неравенства (рис. 58). Решением неравенства служит объединение интервалов: (–5; –1) (–1; 0) (2; 3) (3; +×).

Рис. 58

141

x = 4 и исследовав изменение зна ов левой части неравенства

(рис. 59), получаем ответ: (–×; –1) (3 ; 3) (4; +×).

--

2

Рис. 59

5. Расположение корней квадратного трехчлена

1°. При решении не оторых задач нам потребуется знание ряда теорем о расположении орней вадратно о трехчлена наоординатной прямой.

2°. Пусть вадратный трехчлен y = ax2 + bx + c имеет действительные орни x1 и x2, а x0 — а ое-нибудь действительное

число. То да справедливы следующие теоремы (см. пп. 3°—5°). 3°. ТЕОРЕМА 1. Чтобы оба орня вадратно о трехчлена были меньше, чем число x0 (т. е. лежали на оординатной прямой левее, чем x0), необходимо и достаточно выполнение усло-

вий (рис. 60, а и б):

4°. ТЕОРЕМА 2. Чтобы один из орней вадратно о трехчлена был меньше числа x0, а дру ой больше числа x0 (т. е.

142

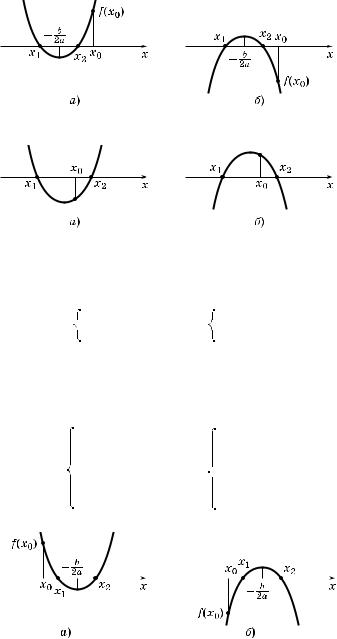
Рис. 60

Рис. 61

число x0 лежало между орнями), необходимо и достаточно выполнение условий (рис. 61, а и б):

5°. ТЕОРЕМА 3. Чтобы оба орня вадратно о трехчлена были больше, чем число x0 (т. е. лежали на оординатной пря-

мой правее, чем x0), необходимо и достаточно выполнение условий (рис. 62, а и б):

Рис. 62

143

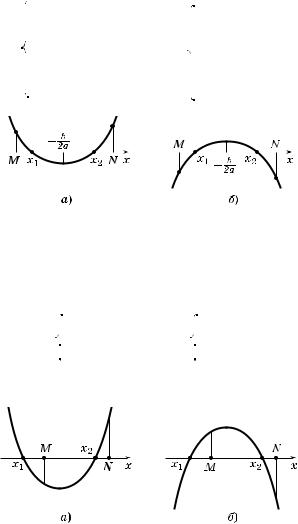
Из приведенных теорем выте ают важные следствия (см. пп. 6°—9°).

6°. С л е д с т в и е 1. Чтобы оба орня вадратно о трехчлена были больше, чем число M, но меньше, чем число N (т. е. лежали в интервале между M и N), необходимо и достаточно выполнение условий (рис. 63, а и б):

Рис. 63

7°. С л е д с т в и е 2. Чтобы толь о больший орень вадратно о трехчлена лежал в интервале (M; N), де M < N, необходимо и достаточно выполнение условий (рис. 64, а и б):

при этом меньший орень лежит вне отрез а [M; N].

Рис. 64

144

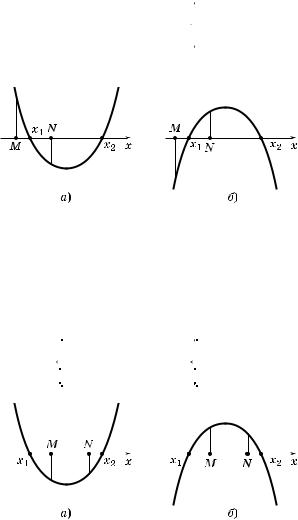
8°. С л е д с т в и е 3. Чтобы толь о меньший орень вадратно о трехчлена лежал в интервале (M; N), де M < N, необходимо и достаточно выполнение условий (рис. 65, а и б):

при этом больший орень лежит вне отрез а [M; N].

Рис. 65

9°. С л е д с т в и е 4. Чтобы один из орней вадратно о трехчлена был меньше, чем M, а дру ой больше, чем N (M < N), т. е. отрезо [M; N] цели ом лежал внутри интервала между орнями, необходимо и достаточно выполнение условий (рис. 66, а и б):

Рис. 66

З а м е ч а н и е. Сформулированные теоремы и следствия очень часто применяются при решении задач с параметрами и поэтому имеют большое значение.

145

146

УПРАЖНЕНИЯ

ж) 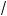x (x + 2)2(x + 3) l 0.

3. На оординатной плос ости xOy изобразите область, о - раниченную линиями: а) осью абсцисс и прямыми y = x, x = 2, x = 4; б) прямыми y = x, y = x + 3, y = –2x + 1 и y = –2x + 5; в) параболами y = x2 и y = 4 – x2; ) убичес ой параболой y = x3

ипрямой y = x; д) параболами y = x2 и y = x ; е) параболой y = x2

иполуо ружностью y = 1 – x2 .

4.На оординатной плос ости xOy изобразите множество точе , оординаты оторых удовлетворяют соотношению:

а) –1 < y < 1; б) x – y > 0; в) y > x2; ) x2 + y2 > 1; д) y l |x2 – x|; е) x2 – 1 m 0; ж) x2 – 3x + 2 = 0; з) |x – y| l 2; и) a2 m x2 + y2 m b2,

де a > 0, b > 0; ) 1 m x m 2, 0 m y m 1 ; л) x2 + y2 m 1, x l 0, y l 0;

--

x

м) 0 m x m 1, 1 – x m y m 1 – x2 .

5. При а их значениях p оба орня уравнения x2 + (2p + 6)x + 4p + 12 = 0

больше (–1)?

6.Определите все значения параметра k, при оторых обаорня уравнения x2 + 4kx + (1 – 2k + 4k2) = 0 меньше (–1).

7.При а их значениях c один из орней уравнения

(c2 + c + 1) x2 + (2c – 3)x + c – 5 = 0

больше 1, а дру ой меньше 1?

8. Определите все значения t, при оторых орни уравнения x2 + x + t = 0 больше t.

147

9.Для а их значений k неравенство x2 + kx + k2 + 6k < 0 выполняется при всех 1 < x < 2?

10.Найдите значения k, при оторых из неравенства

kx2 – x + 1 < k < 0 следует неравенство 0 < x < 1.

11.Найдите все значения параметра a, при оторых обаорня уравнения x2 – 2ax – 1 = 0 по модулю не превосходят 2.

12.Найдите все значения параметра k, при оторых оба

орня уравнения x2 – 6k + 2 – 2k + 9k2 = 0 больше 3. 13. При а их значениях параметра a уравнение

ax2 – (a + 1)x + 2 = 0

имеет два различных орня, оторые по модулю меньше 1? 14. При а их значениях параметра p уравнение

x2 + 2(p – 3) + 9 = 0

имеет два различных орня, оторые принадлежат интервалу (–6; 1)?

15. При а их значениях параметра k неравенство

x2 + (4k – 5)x + 3k2 – 5k > 0 справедливо для всех x та их, что 1 m x m 4?

Задания для повторения

16.Из сосуда вместимостью 54 л, наполненно о ислотой, вылили нес оль о литров и долили сосуд водой, затем снова вылили столь о же литров смеси. То да в оставшейся в сосуде смеси о азалось 24 л чистой ислоты. С оль о ислоты вылили в первый раз?

17.Для перевоз и 60 т руза из одно о места в дру ое затребовали не оторое оличество машин. Ввиду неисправности доро и на аждую машину пришлось рузить на 0,5 т меньше, чем предпола алось, поэтому дополнительно потребовалось добавить 4 машины. Ка ое оличество машин было затребовано первоначально?

18.Имеет ли смысл выражение:

а) (–5)–1/7; б) (–3)–4; в) 52/3; ) 0–2/3?

19. Найдите область определения выражения: а) (a + 1)–2/5; б) x3/5; в) a–3/4; ) (a – 5)2/3.

148

20.Верно ли, что сумма и произведение чисел a и b являются рациональными числами, если:

а) a и b — рациональные числа; б) a и b — иррациональные числа?

21.Расположите данные числа в поряд е возрастания. У а- жите, а ие из них являются рациональными, а а ие — ирра-

< 3; )) –5 < x < –3, 3 < x < 5; д) –× < x m –3,5, –2 m x m –1, 0,5 m x < +×;

е) –× < x < 1, 1 < x < 9. 2. а) x = 0, 3 m x m 4, x > 6; б) –2 < x m –1,

--

2

17. 20 машин. 18. а) Да; б) да; в) да; )) нет. 19. а) a Ý R, a − –1; б) x Ý R;

ное.

Решения и методичес ие у азания

К упражнению 1а

1. Найдем точ и, в оторых выражения, записанные под зна ом

2. Эти точ и разбивают числовую прямую на три промежут а:

149

3.Рассмотрим данное неравенство на промежут е –×; –5 и ре-

-2-

шим полученную систему:

К упражнению 1

1. Положим y = |x|; то)да данное неравенство примет вид (y – 3)(y – 5) < 0.

150