
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf

4. Решив неравенство a – a + x l 0, получим: |
|
x m a(a – 1). |
(2) |
5.Та а x l 0, то с учетом с азанно)о ранее за лючаем, что неравенство (2) справедливо при a = 0 или при a l 1.
6.Сведем уравнение (1) системе уравнений с помощью подста-
нов и t = 
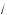 a + x , )де t l 0. Из уравнения (1) получаем x =
a + x , )де t l 0. Из уравнения (1) получаем x = 
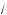 a – t l 0 и приходим системе
a – t l 0 и приходим системе
t =  a + x ,
a + x ,
(3)
x =  a – t .
a – t .
7. Возведя в вадрат оба уравнения системы (3), получим
 t2 = a + x,
t2 = a + x,
(4)
x2 = a – t.
8. Вычитая второе уравнение системы (4) из перво)о, имеем
t2 – x2 = x + t, т. е. (t + x)(t – x – 1) = 0. (5) 9. Рассмотрим уравнение (5). Та а t l 0 и x l 0, то t – x – 1 = 0;
после обратной замены t на 
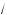 a + x получим уравнение
a + x получим уравнение 
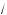 a + x = x + 1; то)да
a + x = x + 1; то)да
|
|
a + x = (x + 1)2, или x2 + x + 1 – a = 0. |
(6) |
|||||||
10. Решив уравнение (6), находим |
|
|
|
|||||||
x |
1 |
= –------1-----–------ |
---4----a-----–-----3-- , |
x |
2 |
= –------1-----+----------4----a----–------3- |
при a l 3-- . |
|
||
|
|
|
2 |
|
|
2 |
4 |
|
||
|
|
|
|
|
|
|
|
|||
11. Проверим найденные значения: |
|
|
|
|||||||
а) x1 не удовлетворяет условию x l 0; |
|
|
||||||||
б) неравенство x |
2 |
= –------1-----+------- |
---4---a-----–------3- l 0 выполняется при |
4a – 3 l 1, |
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. при a l 1.
Ответ: если a = 0, то x = 0; если a Ý [1; +×), то уравнение имеет
единственный орень x = |
–------1-----+-- 4a – 3 ; если a Ý (–×----------------------- ; 0) (0; 1), то |
||||||
|
|
2 |
|
||||
уравнение не имеет орней. |
|
||||||
К упражнению 2м |
|
|
|
|
|
|
|
1. |
Решим уравнение |
|
|
|
|
|
|
|
|
2 |
|
x |
|
– x2 = a. |
(1) |
|
|
|
|
||||
2. |
Если a < 0, то уравнение (1) не имеет решений. |
|
|||||
172 |
|
|
|
|
|
|
|



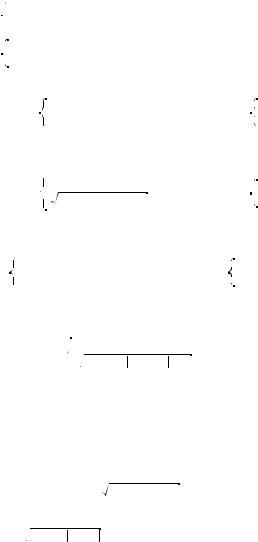






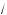 3x ·
3x · 
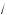 a – 3x = 1, или 2
a – 3x = 1, или 2
 3x(a – 3x) = a – 1. (2)
3x(a – 3x) = a – 1. (2)
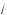 a + x l 0.
a + x l 0.
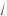 1 – a
1 – a
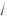 1 – a
1 – a
 1 – a
1 – a
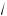 1 – a
1 – a
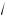 1 – a
1 – a
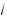 1 – a
1 – a
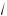 1 – a
1 – a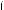 x = 4,
x = 4,
 y + |x – 3| = 2.
y + |x – 3| = 2.
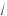 25 – x
25 – x 3 m x m 5,
3 m x m 5,

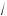 25 – x
25 – x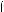 –5 m x < 3,
–5 m x < 3,

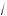 25 – x
25 – x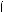 x = 0,1,
x = 0,1,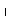

 25 0,1 0,1 – 1 + 4 = 5 · 0,1 – 3.
25 0,1 0,1 – 1 + 4 = 5 · 0,1 – 3.
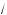 4 – 7x x + 2 = 3x + 2
4 – 7x x + 2 = 3x + 2  2x – 2
2x – 2
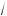 x
x (
(
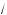 x + 4 –
x + 4 – 
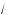 x – 4)
x – 4)
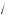 x + 4 –
x + 4 – 
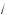 x – 4 |.
x – 4 |. x l 4,
x l 4,

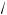 x + 4 –
x + 4 – 
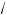 x – 4 l 0,
x – 4 l 0,

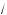 x + 4 –
x + 4 – 
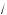 x – 4 + x = 16 +
x – 4 + x = 16 + 
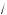 x + 4 – 2
x + 4 – 2
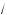 x – 4 ;
x – 4 ; x l 4,
x l 4,

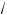 x + 4 –
x + 4 – 
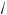 x – 4 < 0,
x – 4 < 0,

 x – 4 –
x – 4 – 
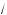 x + 4 + x = 16 +
x + 4 + x = 16 + 
 x + 4 – 2
x + 4 – 2
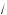 x – 4 . 4. Решим систему (а):
x – 4 . 4. Решим систему (а): x l 4,
x l 4, 8 l 0,
8 l 0,

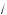 x – 4 = 16 – x.
x – 4 = 16 – x.
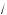 11x + 3 +
11x + 3 + 
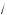 x – 2 =
x – 2 = 
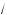 9x + 7 +
9x + 7 + 
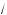 2 – x .
2 – x .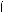 x l 1,
x l 1,
 x
x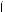 x m 0,
x m 0,
 x
x x l 1,
x l 1, 3x
3x