
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdf
2.Решением это)о неравенства является интервал 3 < y < 5.
3.Вернемся переменной x и получим неравенство 3 < |x| < 5. Это двойное неравенство запишем в виде системы и решим ее:
|x| < 5, |
или |
|
–5 < x < 5, |
|
|||
|x| > 3, |
|
x < –3, x > 3. |
|
|
Ответ: x Ý (–5; –3) (3; 5).
К упражнению 2а
1. Требуется решить неравенство
(2x – 3) x2(4 – x)3 |
m 0. |
(1) |
||
(---x-----–-----6----)--5----(--x----2---- |
+------4----x-----+------6----) |
|||
|
|
|||
2. Квадратный трехчлен x2 + 4x + 6 > 0 при всех x Ý R, та а a > 0 и D < 0, поэтому неравенство (1) равносильно следующему:
x2(2x – 3)(4 – x)3 |
m 0. |
(2) |
|
----------------(--x-----–-----6----)--5---------------- |
|||
|
|
3. При решении неравенств обязательно надо обращать внимание на степень с четным по азателем. В неравенстве (2) имеется та ая степень — это x2. Та а неравенство (2) — нестро)ое, то значение x = 0 является е)о решением.
4. Учитывая с азанное, получаем неравенство
(2x – 3)(4 – x)3 |
m 0. |
(3) |
|
------------(--x------–-----6----)--5------------ |
|||
|
|
5. На числовой прямой отметим точ и, в оторых дробь в левой части неравенства (3) обращается в нуль или имеет разрыв. Это точ и
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = -- , x = 4, x = 6, оторые разбивают числовую прямую на четыре |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
, |
3 |
, (4; 6) и (6; +×). |
|
|
|
|
|
|
|
|
промежут а: –×; -- |
-- ; 4 |
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
6. Определяем зна и неравенства (3) на аж- |
|
|
|
|
|
|
|
|
|||||
дом из у азанных промежут ов и получаем тре- |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
буемое решение (рис. 67). |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
3 |
m x m 4, x |
> 6. |
|
|
|
|
|
|
|
|
|||
Ответ: x = 0, -- |
|
|
|
Рис. 67 |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
151

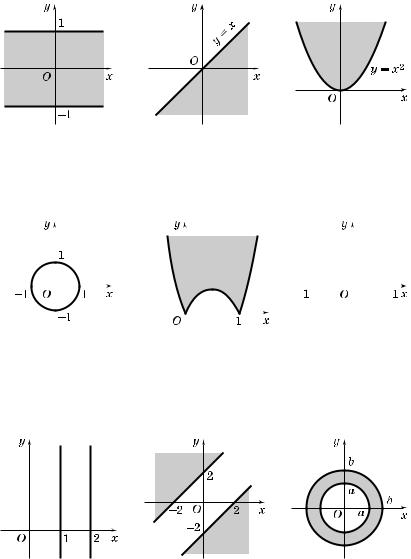
К упражнениям 3а—е
См. соответственно рис. 68—73.
Рис. 68 |
Рис. 69 |
Рис. 70 |
Рис. 71 |
Рис. 72 |
Рис. 73 |
152
К упражнениям 4а—м |
|
|
См. соответственно рис. 74—85. |
|
|
Рис. 74 |
Рис. 75 |
Рис. 76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 77 |
|
|
|
Рис. 78 |
|
|
|
|
|
Рис. 79 |
|
||||
Рис. 80 |
Рис. 81 |
Рис. 82 |
153

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 83 |
|
Рис. 84 |
Рис. 85 |
|||||
К упражнению 5
1. Здесь a (первый оэффициент уравнения) равен 1, т. е. a > 0. Используя теорему 3 (см. с. 143), запишем систему неравенств
D l 0, |
|
|
|
|
b |
|
|
|
(2p + 6)2 – 4(p + 12) l 0, |
|
|
|
||
–------ |
> –1, |
т. е. |
|
–(p + 3) > –1, |
2a |
|
|
||
|
|
1 – (2p + 6) + 4p + 12 > 0. |
||
f(–1) > 0, |
|
|
||
|
|
|
||
2. Решив эту систему, находим –3,5 < p m –3.
К упражнению 6
1. Здесь a = 1 > 0. Применяя теорему 1 (см. с. 142), составим систему
D l 0, |
|
|
|
|
b |
|
|
|
4k2 – (1 – 2k + 4k2) l 0, |
|
|
|
||
–------ |
< –1, |
т. е. |
|
–2k < –1, |
2a |
|
|
||
|
|
1 – 4k + (1 – 2k + 4k2) > 0. |
||
f(–1) > 0, |
|
|
||
|
|
|
||
2. Решив эту систему, получим k > 1.
К упражнению 7
1.Здесь a = c2 + c + 1 > 0 при c Ý R.
2.Со)ласно теореме 2 (см. с. 142, 143), имеем
f(1) = c2 + c + 1 + 2c – 3 + c – 5 < 0.
3. Решив это неравенство, находим –2 – 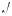 11 < c < –2 +
11 < c < –2 + 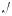 11 .
11 .
К упражнению 8
1. Со)ласно условию, данное уравнение имеет два орня, оторые больше t, поэтому )рафи вадратно)о трехчлена x2 + x + t имеет вид, изображенный на рис. 86.
154

2. Используя теорему 3, запишем систему неравенств
 1 – 4t > 0,
1 – 4t > 0,
t < –1 ,
--
2
t(t + 2) > 0.
Рис. 86
3. Решением этой системы является промежуто t < –2.
К упражнению 9
1. Чтобы неравенство x2 + kx + k2 + 6k < 0 имело место при всех 1 < x < 2, т. е. чтобы интервал (1; 2) лежал между орнями вадратно- )о трехчлена f(x) = x2 + kx + k2 + 6k, нужно, чтобы выполнялись требования следствия 4:
 f(1) m 0,
f(1) m 0, 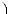 f(2) m 0.
f(2) m 0.
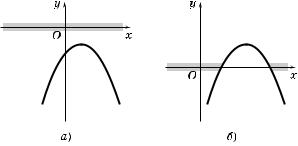
2. Отметим, что здесь записаны нестро)ие неравенства, пос оль у возможно не толь о расположение параболы, у азанное на рис. 87, а, но и расположения, изображенные на рис. 87, б— . В последних трех случаях один или оба орня вадратно)о трехчлена мо)ут совпадать с точ ами x1 = 1 или x2 = 2, но внутренние точ и интервала между
орнями удовлетворяют неравенству 1 < x < 2. 3. Ита , имеем систему неравенств
 f(1) = 1 + k + k2 + 6k m 0,
f(1) = 1 + k + k2 + 6k m 0, 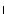 f(2) = 4 + 2k + k2 + 6k m 0.
f(2) = 4 + 2k + k2 + 6k m 0.
4. Решив эту систему, получим –------7-----–-----3--------5-- |
m k m 2 |
3 – 4. |
2 |
|
|
Рис. 87
155
К упражнению 10
1. Со)ласно условию, требуется найти все значения k, при оторых любое число x, удовлетворяющее неравенству
kx2 – x + 1 – k < 0, |
(1) |
удовлетворяет и неравенству
0 < x < 1. |
(2) |
2.Это означает, что неравенство (1) достаточно для выполнения неравенства (2), а неравенство (2) необходимо для выполнения неравенства (1).
3.По ажем, что число k должно быть положительным.
а) Если k < 0, то вадратное неравенство (1) выполняется либо при всех x (рис. 88, а), либо при тех x, оторые лежат вне отрез а, содержаще)о орни вадратно)о уравнения kx2 – x + 1 – k = 0 (рис. 88, б).
Рис. 88
б) В аждом из рассмотренных случаев обязательно найдутся значения x, удовлетворяющие условию (1), но не удовлетворяющие условию (2), т. е. в этих случаях условие (2) не является необходимым для выполнения условия (1).
в) Если k = 0, то из неравенства (1) следует, что x > 1, а это противоречит неравенству (2).
4.Ита , k > 0. Та а D = 1 – 4k(1 – k) = (1 – 2k)2 l 0 при любых k, то решения неравенства (1) за лючены между орнями вадратно)о трехчлена.
5.В результате приходим следующим выводам:
а) чтобы выполнялись требования задачи, нужно, чтобы интервал (0; 1) лежал между орнями вадратно)о трехчлена;
156

б) последнее означает, что должны выполняться требования следствия 4.
6. Составим систему уравнений
 f(0) = 1 – k m 0,
f(0) = 1 – k m 0,
 f(1) = k – 1 + 1 – k m 0
f(1) = k – 1 + 1 – k m 0
(в оторой оба неравенства являются нестро)ими; см. решение упр. 9). Отсюда находим k l 1.
К упражнению 16
1. Пусть в первый раз было вылито x л ислоты. То)да в сосуде осталось (54 – x) л ислоты.
2. Долив сосуд водой, получили 54 л смеси, в оторой растворилось (54 – x) л ислоты.
3. Значит, в 1 л смеси содержится 54 – x л ислоты ( онцентра-
----------------
54
ция раствора).
4. Во второй раз из сосуда вылили x смеси, в этом оличестве сме-
си содержится 54 – x · x л ислоты.
----------------
54
5. Та им образом, в первый раз было вылито x л ислоты, во вто-
рой раз 54 – x · x л ислоты, а все)о за два раза вылили 54 – 24 = 30 л
----------------
54
ислоты.
6. Составим уравнение
x + 54 – x · x = 30,
----------------
54
от уда x1 = 18; x2 = 90. Ясно, что x = 90 не удовлетворяет условию. Ита , в первый раз вылили 18 л ислоты.
К упражнению 18 |
|
|
|
а) (–5)–1/7 = 7 (–5)–1 |
= 7 |
–-1- ; |
|
|
|
|
5 |
1 |
1 |
; |
|
б) (–3)–4 = -------------- = |
------ |
|
|
(–3)4 |
81 |
|
|
в) 52/3 = 3 52 ;
52 ;
|
1 |
— не имеет смысла. |
)) 0–2/3 = ---------- |
||
0 |
2/ 3 |
|
157

К упражнению 19
а) (a + 1)–2/5 = |
|
1 |
= |
1 |
, )де a − –1; |
|||
(---a-----+------1----)--2/5------ |
5------(--a-----+------1----)--2- |
|||||||
|
|
|
|
|||||
б) x3/5 = 5 x3 , )де x Ý R; |
|
|
||||||
в) a–3/4 = ---- |
1------ |
= ---- |
1------ , )де a > 0; |
|
||||
a |
3/ 4 |
4 |
a |
3 |
|
|
|
|
|
|
|
|
|
|
|
||
)) (a – 5)2/3 = 3 (a – 5)2 , )де a Ý R.
(a – 5)2 , )де a Ý R.
К упражнению 20
а) Если a и b — рациональные числа, то сумма a + b и произведение ab та же числа рациональные.
б) Если a и b — иррациональные числа, то сумма a + b та же число иррациональное (за ис лючением случая, о)да a = –b), а произведение ab может быть а рациональным, та и иррациональным чис-
лом (например, 
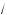 3 ·
3 · 
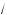 7 =
7 = 
 21 — число иррациональное, а
21 — число иррациональное, а 
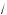 7 ·
7 · 
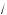 7 — рациональное).
7 — рациональное).
158

Т е м а 10
À
Обратная функция. Степенная функция с целым показателем.
Функция y = k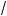 x .
x .
Иррациональные уравнения. Иррациональные неравенства
Теоретичес ие сведения
1. Обратная функция
1°. Пусть фун ция y = f(x) монотонна в своей области определения D(f). То да аждому x Ý D(f) соответствует единственный y Ý E(f) и обратно, аждое значение y Ý E(f) соответствует единственному x Ý D(f). Значит, в этом случае можно построить новую фун цию, определенную на E(f) и та ую, что аждому y Ý E(f) ставится в соответствие x Ý D(f), удовлетворяющее уравнению y = f(x). Эту новую фун цию называют обратной по отношению фун ции y = f(x).
2°. Для нахождения фун ции, обратной данной y = f(x), на- |
|
до выразить x через y: x = g(y), а затем записать полученную |
|
фун цию в общепринятой форме y = g(x). |
|
3°. Отметим, что если фун ции y = f(x) и y = g(x) являются |
|
взаимно обратными, то область определения фун ции f совпа- |
|
дает с множеством значений фун ции g |
|
и, наоборот, область определения фун - |
|
ции g — с множеством значений фун - |
|
ции f, т. е. D(f) = E(g) и D(g) = E(f). |
|
4°. Графи и взаимно обратных фун - |
|
ций симметричны относительно прямой |
|
y = x (рис. 89). |
|
5°. Рассмотрим, например, фун цию |
|
y = x2, заданную на промежут е (–×; 0]. |
|
На этом промежут е фун ция убывает |
|
и принимает все значения из множест- |
|
ва [0; +×). Следовательно, для данной |
Рис. 89 |
|
159 |

|
фун ции существует обратная. Из урав- |
||||
|
нения y = x2 находим x = |
y или x = |
|||
|
= – y ; та |
а |
переменная x может |
||
|
принимать |
толь о неположительные |
|||
|
значения, то ис омая обратная фун - |
||||
|
ция имеет вид x = – y . Поменяв обо- |
||||
|
значения x на y и y на x, получим фор- |
||||
Рис. 90 |
мулу y = – |
x , де x l 0, с помощью |
о- |
||
|
торой и задается обратная фун ция. |
|
|||
Если же рассматривать фун цию y = x2, заданную на про- |
|||||
межут е [0; +×), то обратной для нее служит фун ция y = |
x , |
||||
де x l 0. На рис. 90 изображены рафи |
фун ции y = x2 при |
||||
x l 0 и рафи |
обратной ей фун ции. |
|
|
|
|
2. Степенная функция с целым показателем |
|
|
|
||
1°. Рассмотрим фун цию, заданную формулой y = xk (k Ý N) и построим ее рафи при различных значениях k. Если k = 1, то получается фун ция y = x, рафи ом оторой является прямая (рис. 91); если k = 2, то получается фун ция y = x2, рафиом оторой является парабола (рис. 92); если k = 3, то получается фун ция y = x3, рафи оторой есть убичес ая парабола
(рис. 93).
На рис. 94 и 95 изображены рафи и фун ции y = xk при k = 4 и k = 5.
Рис. 91 |
Рис. 92 |
Рис. 93 |
160
