
Готовимся к экзамену по математике_Крамор В.С_2008 -544с
.pdfЗначит, если положить δ = ε , то выполнение неравенства
--
2
|x – 2| < δ влечет за собой выполнение неравенства |(2x – 1) – 3| < < ε. Та им образом, со ласно определению, за лючаем, что lim (2x – 1) = 3.
x º 2
4°. ТЕОРЕМА. Если фун ция f(x) имеет предел при x º a, то этот предел — единственный.
5°. Пра тичес и предел фун ции находят не на основании е о определения, а с помощью теорем о пределе фун ции, анало ичных теоремам о пределе числовой последовательности.
6°. Теоремы о пределе суммы, произведения и частно о. Если при x º a существуют пределы фун ций f и g, то:
1) lim (f(x) + g(x)) = lim f(x) + lim g(x);
x º a
2)lim
xº a
3)lim
xº a
|
x º a |
x º a |
||
(f(x)g(x)) = lim |
|
f(x) · |
lim g(x); |
|
|
x º a |
|
x º a |
|
f(x) |
lim f(x) |
|
|
|
x → a |
, |
де |
lim g(x) − 0; |
|
----------- |
= ----------------------- |
|||
g(x) |
lim g(x) |
|
|
x º a |
x → a
4) lim kf(x) = lim k · lim f(x) = k · lim |
f(x), де k — постоян- |
|||
x º a |
x º a |
|
x º x0 |
|
ный множитель. |
|
|
|
|
Из этих теорем выте ает, в частности, что предел мно очле- |
||||
на P(x) при x º x0 равен P(x0), т. е. lim |
P(x) = P(x0). |
|||
|
|
|
x º x0 |
|
Пример. Найти: а) |
lim |
x4 + 2 |
; б) |
x3 + 1 |
------------------- |
lim ---------------- . |
|||
|
x º –2 3x3 – 1 |
x º –1 x + 1 |
||
Р е ш е н и е. а) Та а |
lim |
(x4 + 2) = (–2)4 + 2 = 18, |
||
x º –2
а lim (3x3 – 1) = 3(–2)3 – 1 = –25, то по теореме о пределе ча-
x º –2 |
|
|
стно о получаем, что lim |
x4 + 2 |
18 |
------------------- |
= –------ . |
|
x º –2 |
3x3 – 1 |
25 |
б) Здесь при x = –1 и числитель, и знаменатель обращаются в нуль; поэтому теоремой о пределе частно о пользоваться
нельзя. Заметим, что x3 + 1
----------------
x + 1
=(x2 – x + 1)(x + 1) . Та а при
---------------------------------------------------
x+ 1
вычислении предела при x º –1 предпола ается, что x − –1, то дробь можно со ратить на x + 1. В результате получим
lim x-----3----+-----1-- |
= |
lim (x2 – x + 1) = (–1)2 – (–1) + 1 = 3. |
x º –1 x + 1 |
|
x º –1 |
391

3. Непрерывность функции
1°. Фун цию f(x) называют непрерывной в точ е x0, если
она определена в не оторой о рестности этой точ и и если предел фун ции при x º x0 равен значению фун ции в этой точ е,
т.е. lim f(x) = f(x0).
xº x0
2°. Фун цию f(x), непрерывную в аждой точ е заданно о промежут а, называют непрерывной на всем промеж т е.
3°. Любые рациональные и иррациональные фун ции непрерывны при всех значениях независимой переменной, приоторых они определены.
Например, фун ция y = x2 непрерывна в любой точ е числовой прямой, а фун ция y = 
 x непрерывна в любой точ е x l 0.
x непрерывна в любой точ е x l 0.
4°. Если фун ция в а ой-либо точ е x0 не определена или ее предел в точ е x0 не равен значению фун ции в этой точ е, то оворят, что фун ция имеет разрыв в точ е x0, а точ у x0 называют точ ой разрыва.
|
|
|
|
|
|
|
k |
|
|
Например, фун ция y = -- непрерывна в любой точ е x − 0, |
|||||||
|
|
|
|
|
|
|
x |
|
а в точ е x = 0 имеет разрыв. |
|
|||||||
|
Примеры. 1. Дана фун ция |
|
||||||
|
|
|
|
|
f(x) = |
|
x + 3 при x > 0, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x – 1 при x m 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти точ у разрыва и значение фун - |
|||
|
|
|
|
|
ции в этой точ е. |
|
||
|
|
|
|
|
Р е ш е н и е. Фун ция имеет разрыв |
|||
|
|
|
|
|
в точ е x = 0, та а при x º 0 предел |
|||
|
|
|
|
|
этой фун ции не существует |
(рис. 177). |
||
|
|
|
|
|
Значение фун ции при x = 0 есть f(0) = |
|||
|
|
|
|
|
= 0 – 1 = –1. |
x + 3 |
||
|
|
|
|
|
2. Вычислить предел lim |
|||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
--------------------------- . |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
x º –3 |
x + 4 – 1 |
|
|
|
|
|
Р е ш е н и е. Здесь при x = –3 и числи- |
|||
|
|
|
|
|
тель, и знаменатель обращаются в нуль, |
|||
|
Рис. 177 |
т. е. применить теорему о пределе частно- |
||||||
392

о нельзя. Умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю:
lim |
- - - - - - - - ( - - x - - - - - + - - - - - - - - - - - - - - - - - - - - - - - - - -3 ) ( x +----4-----+------1---)-------- = |
lim (---x-----+------3----)--(-------x-----+------4-----+-----1----) |
= |
||
x º –3 ( x + 4 – 1)( x + 4 + 1) |
x º –3 |
(x + 4) – 1 |
|
||
= ---------------------- |
lim ( x + 3 ) (-----x-----+------4-----+-----1----) |
= lim ( |
x + 4 + 1). |
|
|
|
x º – 3 |
x + 3 |
x º –3 |
|
|
Фун ция 
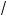 x + 4 + 1 определена в точ е x = –3 и, следовательно, непрерывна в этой точ е. Поэтому ее предел при x º –3 равен значению фун ции при x = –3. В результате получаем
x + 4 + 1 определена в точ е x = –3 и, следовательно, непрерывна в этой точ е. Поэтому ее предел при x º –3 равен значению фун ции при x = –3. В результате получаем
lim (
 x + 4 + 1) =
x + 4 + 1) = 
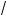 – 3 + 4 + 1 = 2.
– 3 + 4 + 1 = 2.
x º –3
4. Определение производной
1°. Производной фун ции f(x) в точ е x0 называют предел отношения приращения ∆f фун ции в точ е x0 приращению ∆x ар умента, о да последнее стремится нулю. Это можно
записать та : |
lim |
∆f(x) |
= f′(x0) (читается: «эф штрих от x0»). |
-------------- |
|||
|
∆x º 0 |
∆x |
|
|
|
|
2°. Из определения производной следует, что фун ция может иметь производную в точ е x0 толь о в том случае, если
фун ция определена в не оторой о рестности точ и x0, в лючая эту точ у.
3°. Необходимым условием существования производной фун ции в данной точ е является непрерывность фун ции в этой точ е.
Заметим, одна о, что обратное утверждение является неверным. Например, фун ция f(x) = |x – 1| непрерывна на (–×; +×), но в точ е x = 1 производной не имеет: можно по азать, что
lim |
∆f(x) |
= |
|
1 при ∆x l 0, |
|
||||
|
||||
∆x º 0 |
∆x |
|
|
–1 при ∆x < 0, |
|
|
|||
|
|
|
|
т. е. данная фун ция не имеет предела при ∆x, стремящемся нулю.
4°. Нахождение производной f′(x) от данной фун ции f(x) называют дифференцированием этой фун ции.
393
5°. Вычисление производной фун ции y = f(x) производится по общему правилу дифференцирования:
а) дают ар ументу x приращение ∆x и, подставив вместо x значение x + ∆x, находят значение фун ции:
y + ∆y = f(x + ∆x);
б) находят приращение фун ции, вычитая из значения фун ции f(x + ∆x) ее первоначальное значение:
∆y = f(x + ∆x) – f(x);
в) делят приращение фун ции ∆y на приращение ар умента ∆x, т. е. составляют отношение
-∆----y- |
= f---(---x-----+------∆----x----)---–------f--(---x----) |
; |
∆x |
∆x |
|
) находят предел это о отношения при ∆x º 0:
lim -∆----y- |
= |
lim |
f---(---x-----+------∆----x----)---–------f--(---x----) . |
∆x º 0 ∆x |
|
∆x º 0 |
∆x |
Найденный предел и есть производная от фун ции y = f(x). Пример. Дана фун ция y = 
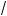 x . Найти y′x = 4.
x . Найти y′x = 4.
Р е ш е н и е. а) y + ∆y = x + ∆x ; |
|
|
|
||||||||
б) ∆y = x + ∆x – x ; |
|
|
|
|
|
||||||
в) -∆----y- = |
-----x-----+------∆----x-- –------------x-- ; |
|
|
|
|
|
|
||||
|
∆x |
∆x |
|
|
|
|
|
|
|
||
) y′ = |
lim -∆----y- = |
lim |
-----x-----+------∆----x-----–------- |
--x-- = |
|
||||||
|
∆x º 0 ∆x |
∆x º 0 |
|
∆x |
|
|
|
||||
= |
lim (-------x-----+------∆----x--- –------------ |
x----)--(----- |
--x------+----∆-----x-----+----------x----) = |
lim |
-----------x-----+------∆----x-----–------x------------ = |
||||||
|
∆x º 0 |
∆x( x + ∆x + x) |
|
|
∆x º 0 ∆x( x + ∆x + x) |
||||||
= |
lim |
------------------1---- |
|
----------- |
---- = ----- |
-----------1---------------- |
= |
-----1----- |
; |
||
|
∆x º 0 |
x + ∆x + x |
|
x + 0 + x 2 x |
|
||||||
д) y′x = 4 |
= 1 |
|
|
= 1 = |
1 . |
|
|
|
|||
|
|
|
|
|
|||||||
|
|
2 x |
|
x = 4 |
2 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||
5. Производная суммы
1°. Пусть u и v — две фун ции, определенные на одном и том же промежут е. То да производная суммы этих фун ций равна сумме их производных, т. е.
(u(x) + v(x))′ = u′(x) + v′(x).
394
2°. Методом математичес ой инду ции до азывается, что эта формула справедлива для любо о онечно о числа сла аемых:
(u1 + u2 + ... + uk)′ = u′1 + u′2 + ... + u′k.
3°. Производная постоянной равна нулю: (C)′ = 0, де C = = const.
Пример. Найти f′(x) если f(x) = x + 5.
Ре ш е н и е. f′(x) = (x + 5)′ = (x)′ + (5)′ = 1 + 0 = 1.
6.Производная произведения
1°. Производная произведения двух фун ций u и v вычисляется по формуле
(uv)′ = u′v + uv′
в предположении, что производные u′ и v′ существуют.
2°. Постоянный множитель можно выносить на зна производной:
(kf(x))′ = kf′(x).
Пример. Найти f′(x), если f(x) = (2x – 3)(3x + 1).
Р е ш е н и е. f′(x) = (2x – 3)′(3x + 1) + (2x – 3)(3x + 1)′ = = 2(3x + 1) + (2x – 3) · 3 = 6x + 2 + 6x – 9 = 12x – 7.
Этот же пример можно решить иначе: f(x) = (2x – 3)(3x + 1) = = 6x2 + 2x – 9x – 3 = 6x2 – 7x – 3; f′(x) = (6x2 – 7x – 3)′ = 12x – 7.
7. Производная частного
Если фун ции u и v имеют в точ е x производные и если
v(x) − 0, то в этой точ е существует производная их частно о u-- |
, |
||||
|
|
|
|
v |
|
оторая вычисляется по формуле |
|
|
|
||
u |
′ |
u′v – uv′ |
|
|
|
-v- |
= |
----------v---2----------- |
. |
|
|
Пример. Найти f′(x), если f(x) = 3------+-----5----x-- . |
|
|
|||
|
|
1 – 3x |
|
|
|
Р е ш е н и е. 3------+-----5----x-- ′ = (---3-----+------5---x-----)′(------1-----–-----3----x----)----–-----(---3----+------5----x----)--(---1-----–-----3----x----)′-- |
= |
||||
1 – 3x |
|
|
(1 – 3x)2 |
|
|
= (---3----′---+-----(---5----x----)′----)--(---1-----–-----3----x----)----–-----(--3-----+------5----x-----)-(---1----′--–------(--3----x----)′-----) = |
|
|
|||
(1 – 3x)2 |
|
|
|
|
|
= 5----(---1-----–-----3----x----)---–------(--3-----+------5----x----)--(---–3-------) |
= ----- |
-----14-------------- . |
|
|
|
(1 – 3x)2 |
(1 – 3x)2 |
|
|
|
|
395

8. Производная степенной функции
1°. Производная степенной фун ции xk, де k Ý Q, x > 0, равна произведению по азателя k на степень xk – 1, т. е.
(xk)′ = kxk – 1. |
(1) |
2°. Заметим, что если k Ý Z, то формула (1) справедлива при всех значениях x Ý (–×; +×), роме x = 0. Если же при этом k > 1, то формула (1) справедлива при любом x.
3°. Из формулы (1) выте ают, в частности, формулы для на-
|
1 |
и y = |
x . |
хождения производных фун ций y = -- |
|||
|
x |
|
|
1 |
получаем: |
|
|
При k = –1 и k = -- |
|
|
|
2 |
|
|
|
1 |
|
′ |
– |
1)′ = (–1)x |
– |
2 |
1 |
(x − |
0); |
(2) |
|
-- |
|
= (x |
|
|
= –----- |
||||||
x |
|
|
|
|
|
|
x2 |
|
|
|
|
( x )′ = (x1/2)′ = |
1 |
= |
1 |
|
1 |
(x > 0). |
(3) |
||||
-- x1/2 – 1 |
-- x–1/2 = ---------- |
||||||||||
|
|
|
2 |
|
2 |
|
2 x |
|
|
||
9. Производная сложной функции
Производная сложной фун ции h(x) = g(f(x)) находится по формуле
h′(x) = g′(f(x))f′(x),
т. е. производная сложной фун ции равна произведению производных фун ций, ее составляющих.
Пример. Найти производную фун ции y = (3 – 5x + x2)100. Р е ш е н и е. y′ = 100 (3 – 5x + x2)99 · (3 – 5x + x2)′ =
= 100(3 – 5x + x2)99 · (–5 + 2x).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Пусть x и x0 — два значе-
ния независимой переменной из D(f). Ка называют и а обозначают разность x – x0?
2. Ка называют разность между новым значением фун ции
f(x0 + ∆x) и ее первоначальным значением f(x0)? Ка им симво-
лом обозначают эту разность?
3. Сформулируйте определения возрастающей и убывающей фун ции, используя понятия
396

приращения ар:умента и приращения фун ции.
4.Что означает запись ∆y =
=f(x2) – f(x1)?
5.Для фун ции y = 2x + 5
найдите: а) x, если x0 = 3 и ∆x =
=0,2; б) ∆y, если x0 = 4 и ∆x = 0,1.
6.Сформулируйте теоремы
о пределе суммы, произведения
ичастно:о фун ций.
7.Найдите предел:
а) |
lim |
(–x3 + 9x2 + x –1); |
||
|
x → 2 |
|
|
|
б) |
lim |
(---x-----–-----4----)---(--x-----+------3----) ; |
||
|
x º –3 x2 + 2x – 3 |
|
||
в) |
lim |
--3----x----2----–-----8----x-----+------4---- |
; |
|
|
x º 2 8 – 14x + 5x2 |
|
||
:) |
lim |
---9-----–-----x---- ; |
|
|
|
x º 9 |
3 – |
x |
|
д) |
lim |
-----x-----–---- |
-----5-- ; |
|
|
x º 5 |
x – 5 |
|
|
|
|
|
|
|
е) |
lim |
3------x-----–-----1-- . |
|
|
|
x º 1 |
x – 1 |
|
|
8.Дайте определение непрерывности фун ции в точ е.
9.Почему рациональная фун ция непрерывна в любой точ е, :де она определена?
10.В а ом случае фун ция имеет разрыв в данной точ е? Ка называют та ую точ у?
11.Постройте :рафи фун -
ции
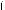 0,5x при x l 1, y =
0,5x при x l 1, y = 
 1 – 3x при x < 1.
1 – 3x при x < 1.
Найдите значение фун ции в точ е разрыва.
12.Дайте определение производной фун ции в данной точ е.
13.Ка ие существуют обозначения для производной фун - ции y = f(x)?
14.Сформулируйте необходимое условие существования производной в данной точ е.
15.Если не оторая фун ция f не является непрерывной в точ-
еx0, то она в этой точ е не имеет
производной (это следует из утверждения п. 4). Верно ли обратное утверждение: «если фун ция непрерывна в точ е x0, то она имеет в этой точ е производную»? Если не верно, то приведите пример.
16.Что называют дифференцированием?
17.Назовите по поряд у все операции, оторые следует произвести при вычислении производной по общему правилу дифференцирования.
18.Дана фун ция y = 2x2 –
–3x. Применяя общее правило дифференцирования, найдите y′(x) и y′(3).
19.Найдите производную фун ции:
а) y = 2x – 5; б) y = 0,6x(x – 2);
в) y = (0,7x + 1)(0,5x – 2); :) y =
|
|
|
1 |
; |
= (3 – 2x)(5x + 4); д) y = ----------------- |
||||
|
|
|
3 + 4x |
|
1 – 3x |
; ж) y |
5x + 1 |
|
|
е) y = ----------------- |
= ----------------- . |
|
||
1 + 2x |
|
2 – 3x |
|
|
20. Найдите |
производную |
|||
фун ции: |
|
|
|
|
а) y = (x – 5)4; |
|
|
||
б) y = 7 – 2x2 + x3 – 3x4; |
|
|||
в) y = |
1 |
; |
4 |
|
----- |
:) y = -- ; |
|
||
|
x2 |
|
x |
|
д) y = |
6 |
; |
е) y = 3x–5; |
|
----- |
|
|||
|
x3 |
|
|
|
ж) y = 3 x2 ; |
2 |
|
||
з) y = ---------- . |
|
|||
|
|
|
x3 |
|
397

21. Найдите область определения сложной фун ции:
а) y = |
1 |
– x2 ; |
б) y = lg (9 – x2); |
||
в) y = |
4 |
– x ; |
|
|
1 |
:) y = |
1-----+------lg------(---3----–------x----) . |
|
22. Ка находится производная сложной фун ции h(x) =
=g(f(x))?
23.Найдите производную сложной фун ции:
а) y = (x2 – 3x + 1)4; б) y = 4 3x3 – 2x + 3 .
3x3 – 2x + 3 .
УПРАЖНЕНИЯ
1. Найдите предел:
а) lim (x3 – 3x2 + 8x + 5); б) |
lim |
|
x2 |
– 2x – 3 |
; в) |
lim |
x2 – 9 |
; |
|||||||||
|
x-----------------------------2 |
– 5x + 6- |
----------------x – 3 |
||||||||||||||
x º 2 |
|
|
|
|
|
|
|
x º 3 |
|
x º 3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
) lim |
x |
|
; |
|
|
|
|
x |
|
|
|
е) |
lim |
x2 – 5x + 4 |
; |
||
|
|
д) lim ------------------------------- ; |
--------------------------------- |
- |
|||||||||||||
x º 0 |
1 + x – 1 |
|
x º 0 |
1 + 3x – 1 |
|
x º × 2x2 – 3x + 7 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ж) lim |
x + x |
; з) |
lim |
3x2 |
|
+ 2 |
. |
|
|
|
|
|
|
|
|
||
----------------- |
|
--------------------------- |
|
|
|
|
|
|
|
|
|
|
|||||
x º 0 |
x – x |
|
x º × x2 + x + 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Найдите производную фун ции: |
|
|
|
|
|
|
|
||||||||||
а) f(x) = |
x + |
|
-------1 ; б) f(x) = 7 x3 ; в) f(x) = x2(5x – 4); |
|
|
||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) f(x) = |
3x2 – 2x + 1 |
; д) y = |
|
3x |
|
; е) y |
= |
|
x |
; |
|
|
|||||
---------------------------------7x |
+ 1 |
- |
|
|
|
-------------------- |
|
|
|
||||||||
|
|
|
|
|
x2 – 1 |
|
|
|
x2 + 4 |
|
|
||||||
ж) y = -------------------- |
9 + x2 |
; з) y = 3 (x3 + 1)2 . |
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Для заданных фун ций f(x) и g(x) найдите значение выражения (g(x)f(x))′ – g(x)f′(x) в у азанной точ е x0, если:
а) f(x) = 2x + 4, g(x) = x2 – 8, x0 = 2,5; б) f(x) = x + 3, g(x) = x2 – 5, x0 = 3,5; в) f(x) = x2 – 8, g(x) = 2x + 4, x0 = 3. 4. Решите уравнение f′(x) = 0, если:
а) f(x) = x4 – 2x2 + 1; б) f(x) = –x5 + 10x3 – 9x.
----- -------------
5 3
Задания для повторения
5. Сначала зарплату повысили на k%, а затем новую зарплату повысили на 2k%. В результате двух повышений зарплата увеличилась в 1,32 раза. На с оль о процентов зарплата была повышена во второй раз?
398
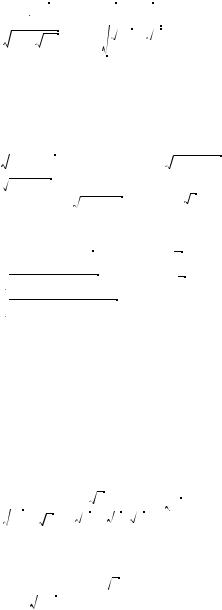
6.В лад, положенный в бан два ода назад, дости 23 328 р. Ка ов был первоначальный в лад при 8% одовых?
7.Сравните числа:
а) a = 
 47 и b =
47 и b = 
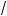 26 +
26 + 
 6 + 1;
6 + 1;
б) 4 9 – 15 и b = ----- |
30--------–----------2- . |
|
2 |
8. Вычислите:
а) bb, если ab = 81, bc = 2, ac = 3; б) ca, если bc = 25, cc = 36, ba = 5; в) ac, если ba = 64, aa = 27, bc = 4.
9. Решите неравенство: |
|
||
а) |
2x – x2 < 5 – x; |
б) 2x + 14 > x + 3; |
|
в) ----- |
8-----–-----10-------x-- l ----- |
-x-----–------5------- ; |
) log (6 – x) m 4. |
|
x – 2 |
8 – 10x |
x |
В ответе запишите наибольшее целое решение. 10. Решите уравнение:
а) 
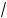 14x – x2 – 40 (cos 2x + 7
14x – x2 – 40 (cos 2x + 7
 3 sin x + 11) = 0; б)
3 sin x + 11) = 0; б) 
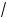 – x2 + 9x – 20 (cos 2x – 5
– x2 + 9x – 20 (cos 2x – 5
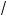 3 sin x – 7) = 0;
3 sin x – 7) = 0;
в) 
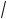 log0,(3)(x – 2) + 1 (5 + cos 2x + 9 cos x) = 0. В ответе у ажите оличество орней.
log0,(3)(x – 2) + 1 (5 + cos 2x + 9 cos x) = 0. В ответе у ажите оличество орней.
11. Решите уравнение (в ответе запишите орень, удовлетворяющий данному неравенству):
а) |
x |
= |
2 + x |
, log1/3 log8 |
2x2 + 12 |
< 0; |
|
x------–-----2-- |
2----x-----–------5- |
------x-----+------1------ |
|||||
|
|
|
|
||||
б) |
106-------------–-----11-------x-- = x + 1, log1/9 x + log3 9x < 3; |
||||||
|
10 – x |
|
|
|
|
||
в) |
2 |
= |
x + 1 |
, log1/2 log6 |
x(x + 1) |
< 0. |
|
x------–-----5-- |
x------+-----11------ |
-----4-----+------x------ |
|||||
12. Упростите выражение до числово о значения:
а) |
x – 1 |
: |
|
x + 1 |
|
– |
x + 7; |
||||||
------------------------- |
-------- |
-------- |
---------------- |
|
|||||||||
|
4 x3 + x |
( x + 4 x)4 x |
|
|
|
|
|
|
|||||
б) |
cos(2π – α) |
|
: 2sin |
|
π |
+ α |
; |
||||||
-cos---------α------–-----sin---------α-----ctg----------0,5---------- |
-- |
||||||||||||
|
α |
|
|
|
2 |
|
|
|
|||||
в) |
1 – x–0,5 |
+ |
1 + ( |
x)–1 |
|
· |
x – 1 |
– 3. |
|||||
1------+---------x----–1---- |
---1----- |
–-----x----–0,5----------- |
|
x------ |
+-------1 |
||||||||
|
|
|
|
|
|||||||||
399

О Т В Е Т Ы
|
1. а) 17; |
б) 4; |
в) 6; |
:) 2; д) |
2-- |
; |
е) |
1-- ; ж) –1; з) 3. |
2. а) -----1---- |
-- – |
||||
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
2 |
x |
– |
1 |
; б) |
3 |
; в) 15x2 – 8x; :) |
21x2 + 6x – 9 |
; д) – |
3 |
; |
||||||
--------------- |
-------------- |
-------(-- |
7----x-----+------1----)--2-------- |
----------------------------- |
||||||||||
|
2x x |
|
77 x4 |
|
|
|
|
|
|
x2 – 1(x2 – 1) |
||||
е) |
|
4 |
; |
ж) – |
9 |
; |
|
з) |
2x2 |
. 3. |
а) 45; |
б) 45,5; |
в) 2. |
|
------------------- |
---------------- |
-------------------- |
|
--------- |
------------ |
|||||||||
|
x2 + 4(x2 + 4) |
x2 x2 + 9 |
|
|
|
3 x3 + 1 |
|
|
|
|
||||
4. а) x1 = 0, x2, 3 = ä1; б) x1, 2 = ä1, x3, 4 = ä3. 5. На 20%. 6. 20 000 р. 7. а) a < b; б) a > b. 8. а) 16; б) 6; в) 3. 9. а) 2; б) 0; в) 1; :) 5. 10. а) Четыре орня; б) три орня; в) 3. 11. а) 4; б) 8; в) 9. 12. а) 6; б) –0,5; в) –1.
Решения и методичес ие у азания
К упражнению 1а
1. Сначала применяем теорему о пределе ал:ебраичес ой суммы и выносим постоянные множители за зна предела, а затем подставляем вместо x е:о предельное значение x = 2:
lim (x3 – 3x2 + 8x + 5) = lim x3 – 3 lim x2 + 8 lim x + 5 =
x º 2 |
x º 2 |
x º 2 |
x º 2 |
=23 – 3 · 22 + 8 · 2 + 5 = 17.
2.Этот предел можно найти проще, если вместо x сразу подставить е:о предельное значение:
lim (x3 – 3x2 + 8x + 5) = 23 – 3 · 22 + 8 · 2 + 5 = 17.
x º 2
К упражнению 1б
1. При x º 3 числитель и знаменатель данной дроби стремятся нулю. Поэтому непосредственное применение теоремы о пределе частно- :о здесь невозможно.
2. Одна о данную дробь можно со ратить:
x2 – 2x – 3
------------------------------
x2 – 5x + 6
=(x – 3)(x + 1)
-------------------------------------
(x – 3)(x – 2)
=x + 1 .
-------------
x – 2
3. Теперь находим ис омый предел:
lim |
------------------------------x2 – 2x – 3 = lim |
x-------------+ 1 |
= 3-------------+ 1 |
= 4. |
x º 3 |
x2 – 5x + 6 |
x – 2 |
3 – 2 |
|
x º 3 |
|
|
|
400
