1.2.3 Гармонический анализ непериодических сигналов

Гармонический анализ периодических сигналов можно распространить на непериодические сигналы. Пусть такой сигнал s(t)задан в виде некоторой функции, отличной от нуля в промежутке(t₁, t₂)(рис. 1.5).

Рис.1.5 Непериодический сигнал

Выделив произвольный отрезок времени Т,включающий в себя проме­жуток(t₁, t₂),мы можем представить заданный сигнал в виде ряда Фурье.

, 0<t<T, (1.43)

где ,а коэффициентыс_пв соответствии с формулой (1.22)

. (1.44)

Подставив (1.44) в (1.43), получим

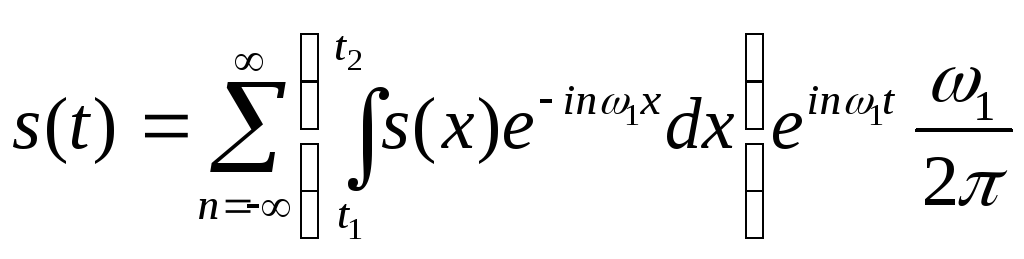, 0<t<T. (1.45)

Здесь учтено, что

Вне отрезка (0, Т)ряд (1.43) определяет функцию, гдеk— целое число, т. е. периодическую функцию, полученную повторе­ниемs(t)вправо и влево с периодомТ.Для того чтобы вне отрезка (0, Т) функция равнялась нулю, величинаТдолжна быть бесконечно большой. Но чем больше отрезокТ,выбранный в качестве периода, тем меньше ко­эффициентыс_п.УстремляяТк бесконечности, в пределе получаем бесконеч­но малые амплитуды гармонических составляющих, сумма которых изобра­жает исходную непериодическую функциюs(t),заданную в интервалеt₁<t<t₂(см. рис.1.5). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при ос­новная частота функции. Иными словами, расстояние меж­ду спектральными линиями (см. рис.1.4), равное основной частотестановится бесконечно малым, а спектр — сплошным.

Поэтому в выражении (1.45) можно заменить нана текущую частоту, а операцию суммирования операцией интегрирования.

Таким образом, приходим к двойному интегралу Фурье

. (1.46)

Внутренний интеграл, являющийся функцией ,

, (1.47)

называется спектральной плотностьюилиспектральной характеристикойфункцииs(t).

В общем случае, когда пределы t₁и t₂и не уточнены, спектральная плот­ность записывается в форме

. (1.48)

После подстановки (1.48) в выра­жение (1.46) получаем:

Между сигналом s(t)и его спектромS()существует однозначное со­ответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изме­нением спектра. Из многочисленных возможных преобразований сигнала рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг сиг­нала во времени, изменение масштаба времени, сдвиг спектра сигнала по частоте, дифференцирование и интегрирование сигнала. Кроме того, будут рассмотрены сложение сигналов, произведение и свертка двух сигналов, а также свойства взаимной обратимостииtв преобразованиях Фурье.

1.2.3.1 Основные свойства преобразования Фурье

1) Сдвиг сигналов во времени

Пусть сигнал s₁(t)произвольной формы существует на интервале вре­мени отt₁доt₂и обладает спектральной плотностьюS₁(). При задержке этого сигнала на времяt₀(при сохранении его формы) получим новую функ­цию времени

_,

существующую на интервале от t₁+t₀доt₂+t₀.

Спектральная плотность сигнала s₂(t)в соответствии с (1.48)

Вводя новую переменную интегрирования =t-t₀,получаем

Из этого соотношения видно, что сдвиг во времени функции s(t)на ±t₀приводит к изменению фазовой характеристики спектраS() на вели­чину ±t₀. Очевидно и обратное положение: если всем составляющим спек­тра функцииs(t) дать фазовый сдвиг 0 () = ±t₀линейно-связанный с частотой, то функция сдвигается во времени на ±t₀.

Амплитудно-частотная характеристика спектра (т. е, модуль спектраль­ной плотности) от положения сигнала на оси времени не зависит.

2. Изменение масштаба времени

Пусть сигнал s₁ (t),изображенный на рис. 1.6 сплошной линией, под­вергся сжатию во времени. Новый сжатый сигналs₂(t)(штриховая кривая на рис. 1.6) связан с исходным соотношением,n>1

Рис. 1.6. Сжатие сигнала при сохранении его амплитуды

Длительность импульса s₂(t) вnраз меньше, чем исходного, и равна_и/п.Спектральная плот­ность сжатого импульса

Вводя новую переменную интегрирования =nt,получаем

Но интеграл в правой части этого выражения есть не что иное, как спектральная плотность исходного сигнала s₁(t) при частоте/п,т. е.S₁(/п).

Таким образом, .

Итак, при сжатии сигнала в праз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается впраз. Очевидно, что при растягивании сигнала во времени (т. е. приn<1) имеют место сужение спектра и увеличение модуля спектральной плотности.