1.2 Математическое описание детерминированных измерительных сигналов. Сигналы и их математические модели

Энергетические характеристики. Основными энергетическими характеристиками вещественного сигналаs(t) являются его мощность и энергия.

Мгновенная мощность определяется как квадрат мгновенного значения s(t):

р(0 =s²(t). р (t)=s²(t).

Если s(f)— напряжение или ток, тор(t) есть мгновенная мощность выделяемая на сопротивлении в 1 Ом.

Энергия сигнала на интервале t₂, t_xопределяется как интеграл от мгно­венной мощности:

. (1.1)

Отношение

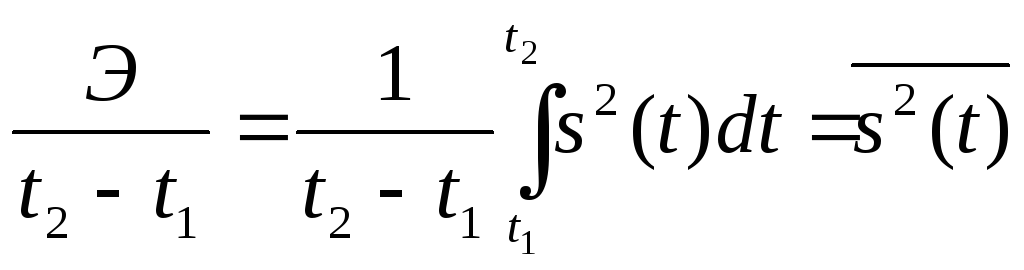(1.2)

имеет смысл средней на интервале t₂, t_xмощности сигнала.

Реальные сигналы имеют конечную длительность и ограниченную по величине мгновенную мощность. Энергия таких сигналов конечна. В теории сигналов часто рассматриваются функции времени, заданные на всей оси времени при конечной величине средней мощности. Говорить об энергии подобных сигналов, обращающейся в бесконечно большую ве­личину, не имеет смысла.

1.2.1 Представление произвольного сигнала в виде суммы элементарных колебаний

Для теории сигналов и их обработки важное значение имеет разложение заданной функции f(х)по различным ортогональным системам функций. Напомним основные определения, относящиеся к свойствам ортого­нальных систем.

Бесконечная система действительных функций

(1.3)

называется ортогональной на отрезке [а, b],если

при _.(1.4)

При этом предполагается, что

, (1.5)

т. е. что никакая из функций рассматриваемой системы (1.3) не равна тож­дественно нулю.

Условие (1.4) выражает попарную ортогональность функций системы (1.3). Величина

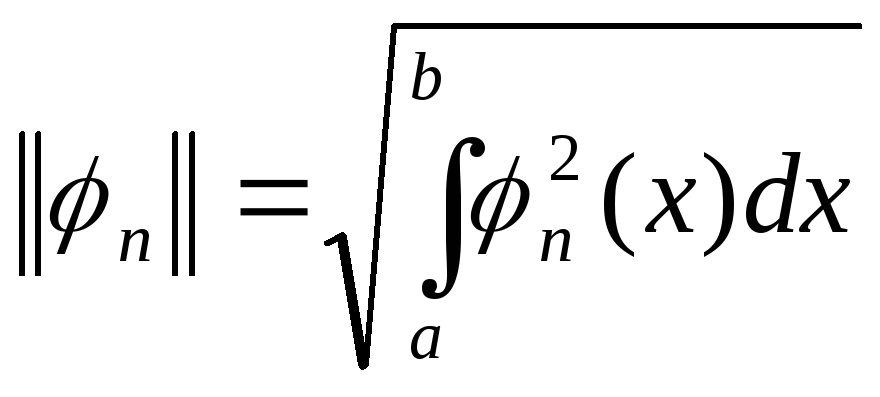(1.6)

называется нормой функций .

Функция , для которой выполняется условие

(1.7)

называется нормированнойфункцией, а система нормированных функцийв которой каждые две различные функции взаим­но ортогональны, называетсяортонормированнойсистемой.

В математике доказывается, что если функции непрерывны, то произвольная кусочно-непрерывная функцияf(x), для которой выполняет­ся условие

может быть представлена в виде суммы ряда

. (1.8)

Интеграл в предыдущем выражении вычисляется по области опреде­ления f(x).

Умножим обе часта уравнения (1.8) на и проинтегрируем в пределахa, b. Все

слагаемые вида приобращаются в нуль в силу ортогональности функцийи. В правой части оста­ется одно слагаемое

,

что позволяет написать

_,

откуда следует важное соотношение

. (1.9)

Ряд (1.8), в котором коэффициенты с_попределены по формуле (1.9), называетсяобобщенным рядом Фурьепо данной системе. Совокупность коэффициентов называетсяспектромсигналаf(x)в ортогональной системеи полностью определяет этот сигнал.

Обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций и фиксированном числе слагаемых ряда (1.8) он обеспечивает наилучшую аппроксимацию (в смысле минимума сред­неквадратической ошибки) данной функции f(x). Это означает, что средне­квадратическая ошибка, под которой подразумевается величина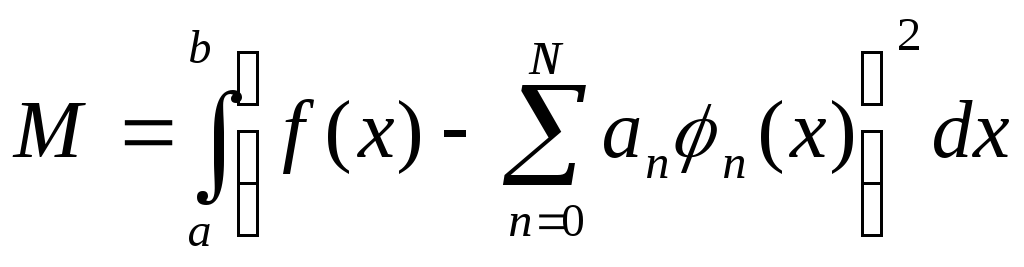,достигает минимума, когда коэффициенты рядаа_п=с_п.

Действительно, подставив в предыдущее выражение а_п=с_n+b_п и использовав равенства (1.4), (1.6) и (1.9), получим

.

Отсюда следует, что Мдостигает минимума приb_п= 0, т. е. приа_п=с_п.Таким образом,

. (1.10)

Так как величина

является квадратом нормы функции , ато на основании (1.10) можно написать следующее неравенство:

. (1.11)

Это основное неравенство, называемое неравенством Бес­селя,справедливо для любой ортогональной системы.

Ортогональная система называется полной,если увеличением числа членов в ряде среднеквадратическую ошибкуМможно сделать сколь угод­но малой.

Условие полноты можно записать в виде соотношения

. (1.12)

При выполнении этого условия можно считать, что ряд (1.8) сходится в среднем,т. е.

. (1.13)

Из этого, однако, еще не следует, что 2 (х) сходится к f(x), т. е.

что

при любых значениях х.

Для системы функций ,принимающих комплексные значения, приведенные выше определения, обобщаются следующим образом:

условие ортогональности: , при;

квадрат нормы функции:

коэффициенты Фурье:

В этих выражениях обозначает функцию, комплексно-сопряженную функции.

Применительно к сигналам s(t),являющимся функциями времени, вы­ражение (1.8) в дальнейшем будет записываться в форме

. (1.14)

В новых обозначениях квадрат нормы функции s(t) по аналогии с (1.6) будет

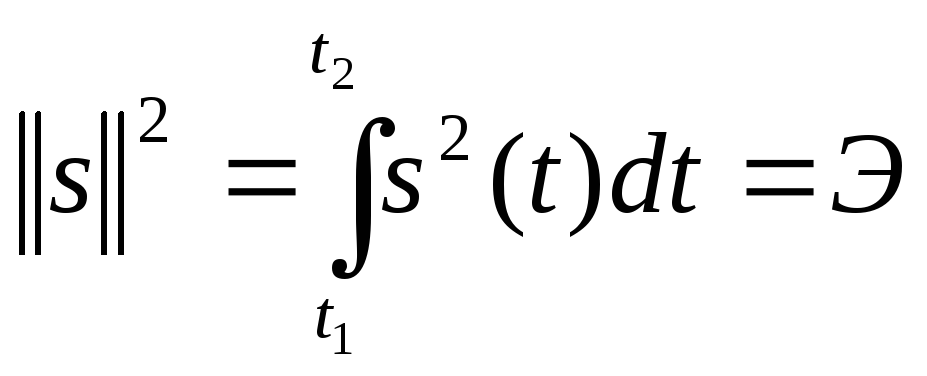. (1.15)

Это выражение совпадает с (1.1).

Таким образом, в соответствии с формулой (1.12) энергия сигнала

, (1.16)

а при использовании ортонормированной системы функций . При этом имеется в виду, что промежуток времениt₂ –t₁котором определяется энергияЭ,являетсяинтервалом ортогональностидля систе­мы функций.

Очевидно, что средняя за время t₂—t₁мощность сигнала

. (1.17)

Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди раз­нообразных задач, требующих разложения сложного сигнала, наиболее важными являются: 1) точное разложение на простейшие ортогональные функции; 2) аппроксимация сигналов, процессов или характеристик, ког­да требуется свести к минимуму число членов ряда (при заданной допусти­мой погрешности).

При первой постановке задачи наибольшее распространение получила ортогональная система основных тригонометрических функций — синусов и косинусов. Это объясняется рядом причин. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою фор­му при прохождении через любую линейную цепь(с постоянными параметра­ми). Изменяются лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать симво­лический метод, разработанный для анализа передачи гармонических коле­баний через линейные цепи. По этим, а также и некоторым другим причинам гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

При второй постановке задачи — приближенном разложении функций — применяются разнообразные ортогональные системы функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра, функции Уолша и многие другие.