1.4.2.1 Спектр колебания при гармонической угловой модуляции

Используем полученные выше результаты для анализа колебания вида

. (1.103)

Это выражение совпадает с (1.98) при модуляции частоты по закону ω(t) = ω₀ + ω_дcost. Начальная фаза, а также начальная фа­за модулирующей функции γ опущены для упрощения выкладок. При не­обходимости они легко могут быть введены в окончательные выражения.

В данном случае . Подставляя ϴ (t) в выражение (1.102), получаем

. (1.104)

Учитывая, что множители cos(тsint) иsin(msint) являются периодическими функциями времени, разложим их в ряд Фурье.

В теории бесселевых функций доказываются следующие соотношения:

Здесь J_n (m)— бесселева функция первого родаn-го порядка от аргумен­тат.

С помощью вышеприведенных соотношений уравнение (1.104) можно приве­сти к виду

(1.105)

или в более развернутой форме

. (1.106)

Таким образом, при частотной и фазовой модуляциях спектр колеба­ния состоит из бесконечного числа боковых частот, расположенных попар­но симметрично относительно несущей частоты ω₀и отличающихся от по­следней наn, гдеп— любое целое число. Амплитудап-й боковой состав­ляющейА_п = J_n (т)A₀, гдеA₀— амплитуда немодулированного колеба­ния, ат — индекс модуляции. Отсюда следует, что вклад различных боко­вых частот в суммарную мощность модулированного колебания определяет­ся величинойт.

Рассмотрим режимы угловой модуляции при малых и больших значе­ниях т. Если

т <<1, так что имеют место приближенные равенства

, то выражение (1.104) переходит в следующее:

(1.107)

Сравним это уравнение с уравнением для амплитудно-модулированного колебания, у которого модулирующая функция (т. е. передаваемое сообще­ние) такая же, как и при ЧМ. Так как выражение (1.107) получено для модуляции частоты по закону , то для удобства сравнения зададим модуляцию амплитуды по аналогичному законуA(t) =A₀(1+Мcost). Тогда амплитудно-модулированное колебание запи­шется в форме

(1.108)

Из сравнения (1.107) и (1.108) видно, что при малых значениях тспектр колебания, как и приAM, состоит из несущей частоты ω₀и двух боковых частот: верхней ω₀+и нижней ω₀-. Единственное отличие заключа­ется в фазировке колебаний боковых частот относительно несущего колебания. ПриAMфазы колебаний боковых частот симметричны относительно несущей частоты, а при угловой модуляции фаза колебания нижней боко­вой частоты сдвинута на 180° [знак минус перед последним слагаемым (1.107)]. Это положение иллюстрируется векторной диаграммой, показанной на рис. 1.14,а.

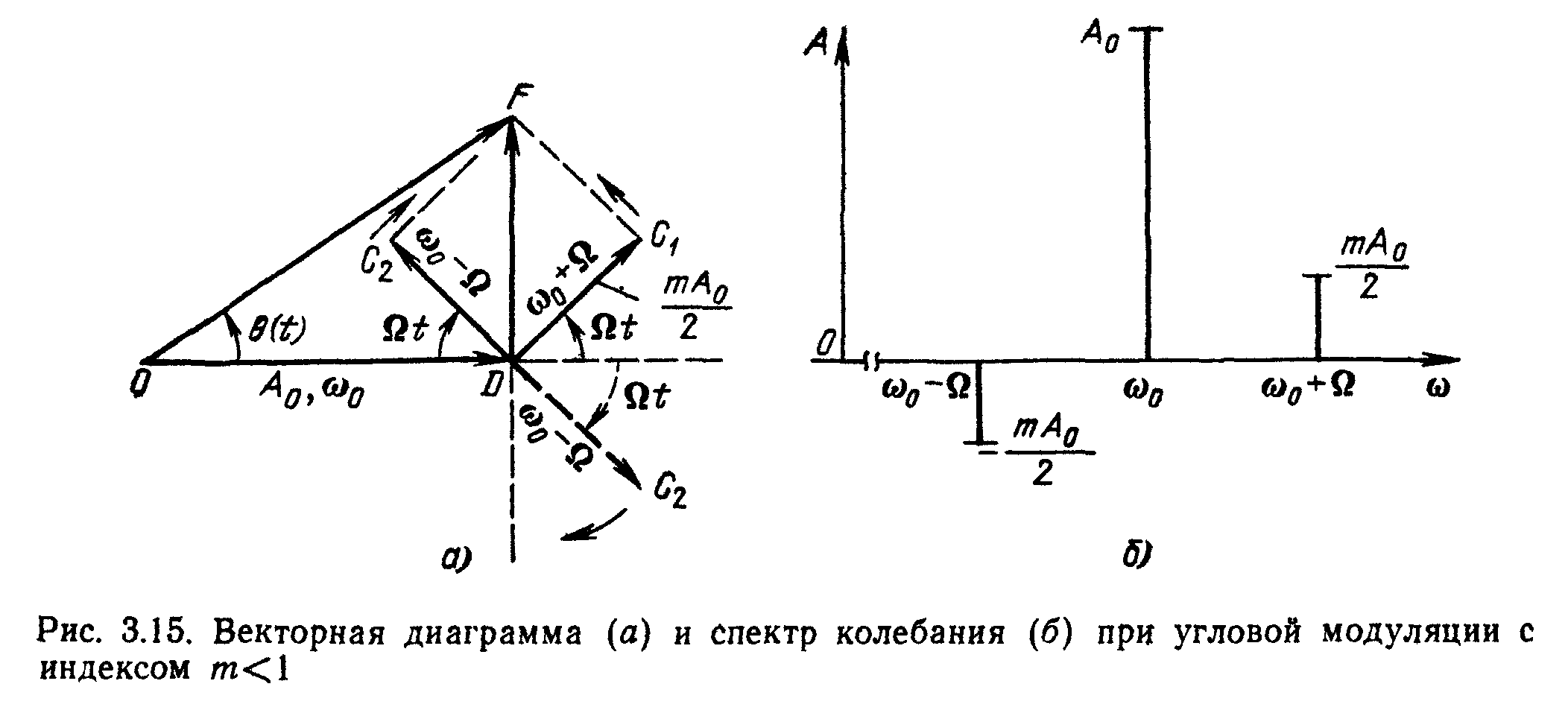
Рис.1.14. Векторния диаграмма (а) и спектр колебания (б) при угловой модуляции с индексом т <<1

Направление вектора DC₂приAMобозначено штриховой линией. Изменение направления этого вектора на 180° приводит к тому, что вектор модуляцииDFвсегда перпендикулярен к направлению вектораOD, изображающего несущее колебание. ВекторOF,изображающий результи­рующее колебание, изменяется как по фазе, так и по амплитуде; однако приамплитудные изменения настолько малы, что ими можно пренебречь и модуляцию можно в первом приближении рассматривать как чисто фазовую.

Спектральная диаграмма для угловой модуляции при т<<1 показана на рис. 1.14,б. Равенство амплитуд колебаний боковых частот сохраняется, а фаза колебания нижней частоты сдвинута на 180°. Амплитуды колебаний боковых частот равныmA₀/2,и поэтому в данном случае индекс модуляциитсовпадает по значению с коэффициентомМ,характеризующим глубину изменения амплитуды приAM: Заметим, что ширина спектра прит<< 1 равна 2, как и приAM. Этот результат показывает, что при очень малых девиациях ω_д(по сравнению с) ширина спектра от ω_дне зависит.

При увеличении фазового отклонения, т. е. при возрастании т,урав­нение (1.107) и диаграмма на рис. 1.14,ане дают правильного представления о действительной картине явлений при частотной или фазовой модуляции.

Рассмотрим теперь большие значения т.Вопрос сводится к выяснению зависимости бесселевой функцииJ_n (т)от порядкового номераппри боль­ших значениях аргументат.Оказывается, что прит>> 1 величина |J_n(т)| более или менее равномерна при всех целых значениях|n|,меньших, чем аргумент τ. При|п|,близких кт, |J_n(т)|образует всплеск, а при дальней­шем увеличении |п|функция |J_n (т)|быстро убывает до нуля. Общий ха­рактер этой зависимости показан на рис.1.15 длят= 100. Из рисунка видно, что наивысший номерпбоковой частоты, которую еще необходимо принимать в расчет, приблизительно равен индексу модуляциит(в данном случаеп= 100).

Рис.1.15. Ширина спектра ЧМ колебания при больших значениях индекса модуля

Приравнивая это максимальное значение п_тахвеличинеm, приходим к выводу, что полная ширина спектра частотно-модулированного колебания

Но т= ω_д/, следовательно, прибольшихиндексах модуляции ширина спектра модулированного колебания близка к удвоенной девиации частоты

. (1.109)

Эта полоса частот обозначена в нижней части рис. 1.16.

Рис.1.16. Спектры колебания при угловой модуляции: а) m=1; б) m=2

Следует отметить, что в соответствии с опреде­лением т[выражение «модуля­ция с малым индексом» эквивалентно вы­ражению «быстрая модуляция», а выраже­ние «модуляция с большим индексом» экви­валентно выражению «медленная модуляция». Поэтому можно сформулировать следующее положение: прибыст­рой угловой модуляции (когдаω_д<<)ширина спектра модулированного ко­лебания близка к значению2;при медленной угловой модуляции(когда ω_д>>)ширина спектра близка к значению2ω_д.