Глава 11

Интервальное оценивание числовых характеристик и параметров распределения генеральной совокупности

Точечные оценки, рассмотренные в предыдущей главе, хотя и являются численными, не дают всей желательной информации об оцениваемых генеральных характеристиках.

Если, например, x¯ = 10, то совершенно неясно, насколько точно число 10 оценивает неизвестное математическое ожидание m. Мы лишь знаем некоторые качественные свойства x¯, такие, как состоятельность и несмещенность которые дают уверенность, что x¯ - хорошая оценка по сравнению с другими возможными. А следовало бы связать точечную оценку с объемом выборки, выработать показатели ее точности и надежности. Эти вопросы решаются в теории интервального оценивания.

11.1Доверительный интервал. Точность и надежность оценки

Пусть θ - неизвестная числовая характеристика или параметр генерального распределения. Определение. Если выполняется соотношение

P (θ1 < θ < θ2) = γ,

то интервал (θ1, θ2) называется доверительным интервалом, который накрывает неизвестную генеральную характеристику θ с доверительной вероятностью γ.

Здесь θ1 = θ1(x1, . . . , xn), θ2 = θ2(x1, . . . , xn) - известные функции выборочных элементов x1, . . . , xn, т.е. статистики. Они вычисляются по выборке.

Число γ называется также надежностью, с которой доверительный интервал накрывает θ. Число α = 1 − γ называется уровнем значимости.

Статистики θ1 и θ2 являются точечными оценками θ. Одна содержит левую, а другая -правую границы, между которыми содержится θ с надежностью γ.

Половину длины доверительного интервала

ε = θ2 − θ1

2

75

называют точностью интервального оценивания.

Пусть известна только одна точечная оценка ˆ генеральной числовой характеристики

θ

или параметра распределения θ.

Определение. Если выполняется соотношение

| − ˆ|

P ( θ θ < ε) = γ,

то число называется точностью, а число - надежностью оценки ˆ генеральной чис-

ε γ θ

ловой характеристики θ.

Здесь ˆ ˆ - статистика, т.е. функция выборочных элементов.

θ = θ(x1, . . . , xn)

Если известны ε и γ, то легко построить доверительный интервал для θ с помощью ее

точечной оценки ˆ.

θ

Как находить ε, γ, строить доверительный интервал (θ1, θ2) в конкретных случаях будет рассмотрено в следующих параграфах, для случаев оценивания математического ожидания m и среднего квадратического отклонения σ.

11.1.1Доверительный интервал для математического ожидания нормальной генеральной совокупности

Известно, что для выборки объема n из нормальной генеральной совокупности случайная

величина √n − 1x¯ − m распределена по закону Стьюдента с n − 1 степенями свободы.

σB

Аналитическое выражение плотности распределения Стьюдента с k степенями свободы дается формулой

свободы порядка 1 +2 γ .

Пример. По выборке объема n = 20 из нормальной совокупности найдены x¯ = 5, 00 и σB = 0, 25. Требуется построить доверительный интервал для m при γ = 0.95.

С помощью таблицы квантилей распределения Стьюдента находим t(1+0.95)/2(20 − 1) = t0.975(19)

76

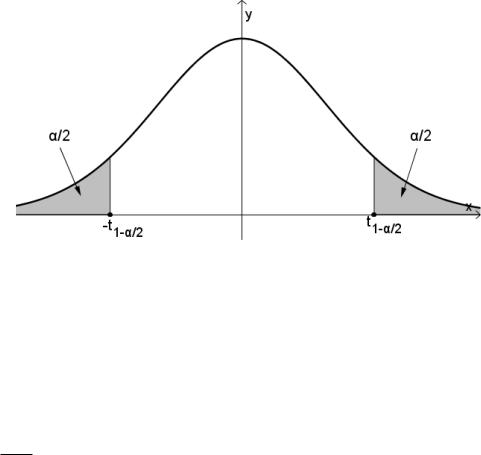
Рис. 11.1: График плотности распределения Стьюдента. Площадь заштрихованных частей в сумме равна α

11.2Доверительный интервал для среднего квадратического отклонения σ нормальной генеральной сово-

купности

Известно, что для выборки объема n из нормальной генеральной совокупности случайная величина nDσ2B распределена по закону χ2 (хи-квадрат) с n − 1 степенями свободы.

Плотность вероятности закона распределения χ2(k) задается формулой

Замечание. Любой доверительный интервал можно построить неоднозначно. Всегда применяется какой-нибудь дополнительный принцип его построения. При построении доверительного интервала для среднего квадратического отклонения σ исходили из принципа, что вероятности попадания χ2 в промежутки левее доверительного интервала и правее его равны между собой.

Пример. Сделано n = 20 измерений контролируемого параметра производимого продукта. По полученной выборке найдено значение выборочного среднего квадратического отклонения σB = 0, 25. Требуется построить доверительный интервал для σ с надежностью

γ = 0, 95.

По таблице распределения хи-квадрат находим

χ2 − (n − 1) = χ2 (19) = 8, 91; χ2 (n − 1) = χ2 (19) = 32, 9.

(1 γ)/2 0,025 (1+γ)/2 0,975

77

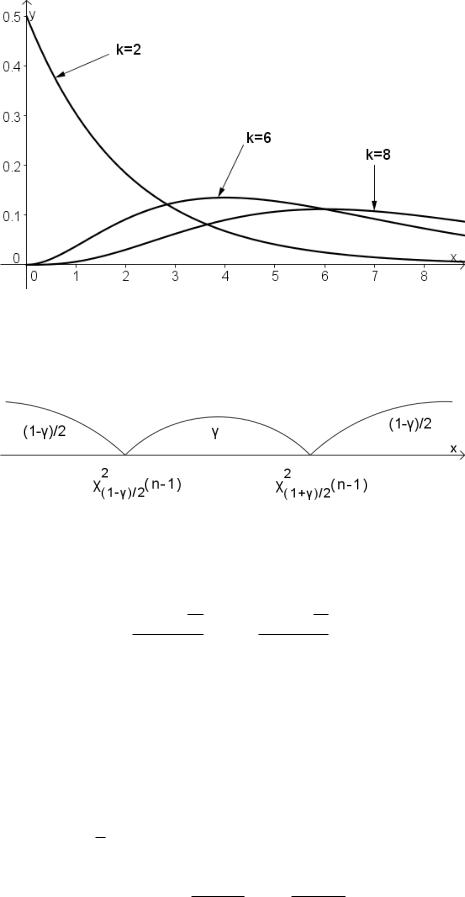
Рис. 11.2: График плотности вероятности распределения хи-квадрат при числе степеней свободы k = 2, 6, 8

Рис. 11.3: Положение доверительного интервала для nDB/s2 на числовой оси

По формуле для доверительного интервала получаем

√√

0, 19 < σ < 0, 36.

11.3Доверительный интервал для математического ожидания m любой генеральной совокупности при боль-

шом объеме выборки

n

Выборочное среднее x¯ = n1 X является суммой большого числа независимых одинаково

i=1

распределенных слагаемых. В силу центральной предельной теоремы при большом объеме

78