Глава 7
Предельные теоремы
Предельные теоремы выясняют асимптотические свойства сумм и средних случайных величин, когда их число стремится к бесконечности. Суммы и средние при этом теряют характер случайности; их поведение можно предсказать с вероятностью, близкой к единице. Предельные теоремы лежат в основе асимптотических методов математической статистики.
7.1 Неравенства Маркова и Чебышёва
7.1.1Неравенство А.А. Маркова
Если X - неотрицательная случайная величина, имеющая конечное математическое ожидание mX , то для любого ε > 0 имеет место неравенство
P (X ≥ ε) ≤ mεX .
Оно дает оценку вероятности попадания случайной величины в промежуток [ε; +∞).
7.1.2Неравенство П.Л. Чебышёва
Если случайная величина X имеет конечные математическое ожидание mX и дисперсию DX , то для любого ε > 0 имеет место неравенство
DX
P (|X − mX | ≥ ε) ≤ ε2 .
Оно дает оценку вероятности попадания случайной величины X в область, лежащую вне промежутка [mX − ε, mX + ε].
Неравенство Чебышёва применяется непосредственно в математической статистике, а также для доказательства теоремы Чебышёва.
7.2 Теоремы Чебышёва и Бернулли
Теорема. (Чебышёва П.Л., 1886г.) для случая одинаково распределенных слагаемых. Пусть случайные величины X1, . . . , Xn попарно независимы, одинаково распределены, имеют математическое ожидание m и дисперсию D. Тогда имеет место предельное
54
соотношение
1 |
n |
Xk − m |
≥ ε n→→∞ 0 ( ε > 0). |
|
P n k=1 |
||||
|
X |
|
||
|
|
|
||
|
|
|
|
|
Теорема Чебышёва носит также название закона больших чисел. Вероятностный смысл ее в том, что арифметическое среднее случайных величин с увеличением числа слагаемых все менее вероятно отклоняется по модулю от своего общего математического ожидания m на любую величину ε.
В математической статистике результаты измерения случайной величины X рассматриваются как одинаково распределенные взаимно независимые случайные величины. Взяв их среднее арифметическое, можно сколь угодно близко приблизиться к искомому математическому ожиданию mX = m с вероятностью, сколь угодно близкой к единице. Теорема Чебышёва лежит в основе этого асимптотического метода математической статистики.
Определение. Последовательность случайных величин X1, X2, . . . , Xn, . . . называется сходящейся по вероятности к величине A (случайной или нет), если для любого ε > 0 имеет место предельное соотношение
P (|Xn − A| ≥ ε) → 0.
n→∞
Теорема Я. Бернулли. Относительная частота P (A) события при n независимых испытаниях по схеме Бернулли стремится по вероятности к вероятности события A при
n → ∞:
P (A) → P (A).
n→∞
Теорема Бернулли теоретически обосновывает возможность приближенного вычисления вероятности события с помощью его относительной частоты.
7.3Центральная предельная теорема для случая одинаково распределенных слагаемых
Определение. Случайная величина X называется центрированной и нормированной, если ее математическое ожидание равно нулю, а дисперсия равна единице.
Любую случайную величину X с конечной дисперсией σX2 и математическим ожиданием mX можно центрировать и нормировать с помощью операции
X− mX .
σ
Теорема (центральная предельная теорема для случая одинаково распределенных слагаемых). Пусть случайные величины X1, . . . , Xn взаимно независимы, одинаково распределены, имеют конечные математическое ожидание m и дисперсию σ2. Тогда функция распределения центрированной и нормированной суммы этих случайных величин
|
n |
n |
n |
||||
Yn = k=1 Xk − Mhk=1 Xki |
= k=1 Xk − mn |
||||||
|
P |
P |
P |
||||
|
s |
h n |
i |
|
σ√ |
n |
|
P
DXk
k=1
55
стремится при n → ∞ к функции распределения нормальной случайной величины с параметрами 0 и 1 (при любом фиксированном x):
FYn (x) = P (Yn < x) n→ Φ (x). |
||||
|
|
→∞ |
|
|
Здесь |
x |
|
|
|
Φ (x) = √2π |
e− 2 |
dt |
||
Z |
||||
1 |
|
t2 |
|
|
−∞
- функция Лапласа.
Замечание. Центральная предельная теорема доказана не только для одинаково распределенных слагаемых, но и при гораздо более общих предположениях, которые обеспечивают, в частности, выполнение требований малости дисперсий слагаемых суммы случайных величин по сравнению с дисперсией всей суммы.
Из теоремы следует, что при достаточно большом n сумма Yn приближенно распределена нормально по закону N(0, 1). Но тогда приближенно распределена нормально и сама
|
k=1 |
|
k=1 |
uk=1 |
|
исходная сумма |
X |
Xk с параметрами |
X |
uX |
DXk. |
n |
n |
MXk и v n |
|||
|
|
|
|
t |
|
Нормальный закон широко распространен в природе. Приведем примеры.
1.Ошибка измерения распределена нормально, так как является суммой большого числа малых ошибок, проистекающих из колебаний параметров среды (температура, влажность, давление и т.д.), колебаний состояния мерительного инструмента, состояния измеряющего субъекта и т.д.
2.По аналогичным причинам распределены нормально координаты точки падения снаряда.
3.Нормально распределена шумовая помеха в управляющем устройстве.
7.4Цепи Маркова. Понятие случайного процесса
Случайный процесс, протекающий в системе S, называется марковским процессом (процессом без последействий), если он обладает следующим свойством: для каждого момента времени t0 вероятность любого состояния системы в будущем (при t > t0) зависит только от ее состояния в настоящем S(t0) и не зависит от того, когда и каким образом система перешла в это состояние.
Состояния системы могут изменяться либо дискретно, либо непрерывно.
Случайный марковский процесс называется процессом с дискретными состояниями, если возможные состояния системы S1, S2, ... Sn можно пронумеровать, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое. Примером такого процесса является процесс, протекающий в техническом устройстве. Можно, например, представить два состояния такой системы: S1 - система работает, S2 - система вышла из строя.
Случайный марковский процесс называется процессом с непрерывными состояниями, если эти состояния меняются непрерывно, постепенно. Примером такого процесса является процесс движения самолета, автомашины.
56
В системе с дискретными состояниями переход от состояния в состояние может происходить в определенные, фиксированные моменты времени либо в случайные моменты.
Случайный марковский процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, заранее фиксированные моменты времени t1, t2, . . . В промежутки времени между этими моментами система S сохраняет свое состояние.
Случайный марковский процесс называется процессом с непрерывным временем, если переход системы из состояния в состояние возможен в любой заранее не известный случайный момент времени.
Так как для марковского процесса с дискретными состояниями и дискретным временем времена t1, t2, . . . , tk, . . . фиксированы, то процесс можно рассматривать как функцию целочисленного аргумента k(k = 1, 2, . . . ) - номера шага. В этом случае переходы системы из состояния в состояние представляют собой последовательность (цепочку) событий или состояний S1(1), S1(2), S3(3), S5(4), S2(5), ... Число в скобках означает номер шага, нижний индекс - номер состояния.
Случайная последовательность событий с фиксированным шагом называется дискретной марковской цепью, если для каждого шага вероятность перехода из любого состояния Si любое другое состояние Sj не зависит от того, когда и как система перешла в состояние Si.
Если переходы системы из состояния в состояние происходят в случайные моменты времени, то соответствующая цепочка состояний называется непрерывной цепью Маркова.
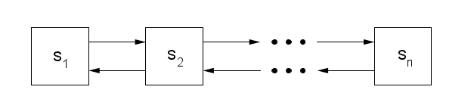
При анализе случайных процессов с дискретными состояниями используют графы состояний. Граф состояний геометрически изображает возможные состояния системы и ее возможные переходы из состояния в состояние.
Рис. 7.1: Марковская цепь. Процесс гибели и размножения
Важное место в исследовании экономических систем занимает процесс гибели и размножения.
Марковская непрерывная цепь называется процессом гибели и размножения, если ее граф состояний представляет собой цепочку, в которой каждое из промежуточных состояний связано прямой и обратной связью с каждым соседним состоянием.
57
Часть II
Математическая статистика
58