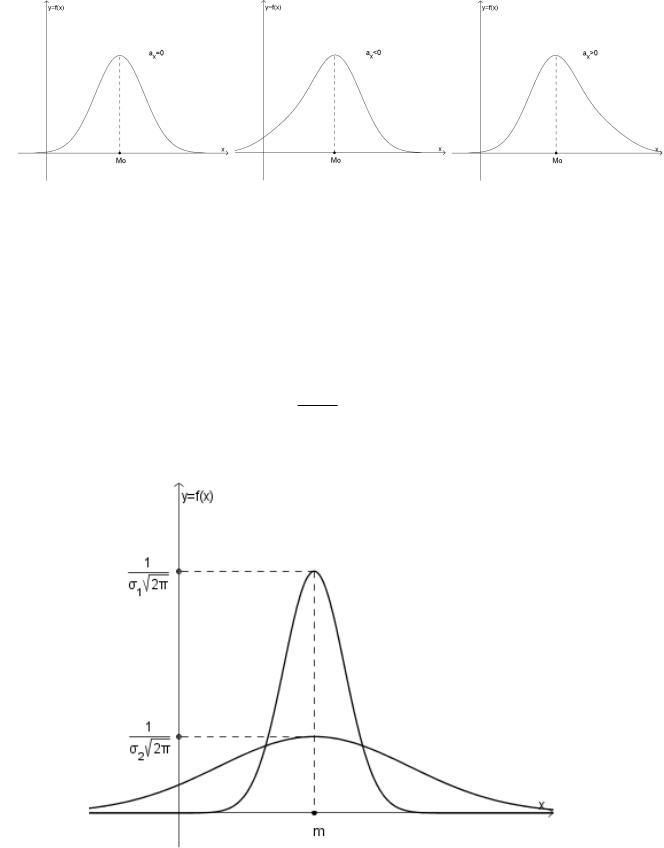
Рис. 5.7: Асимметрия распределения

5.7Нормальное, показательное, равномерное распределения

5.7.1Нормальное распределение (закон Гаусса)

Случайная величина X называется распределенной нормально, если ее плотность вероятности задана формулой

σ 2π

Параметр m называется центром, а параметр σ - стандартным отклонением случайной величины X.

Рис. 5.8: График плотности нормального распределения (σ2 > σ1)

40

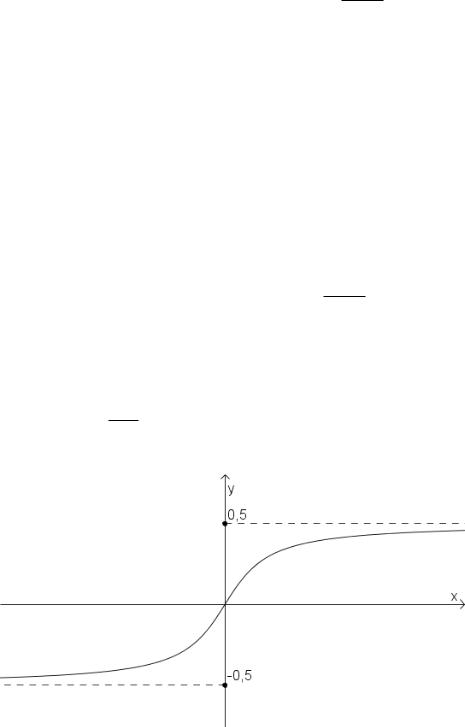
Нормальный закон распределения обозначается символом N(m, σ). Функция распределения нормального закона выражается формулой

функция Лапласа.

В некоторых случаях бывает удобно использовать функцию Лапласа в виде

тогда функция распределения нормально распределенной случайной величины выражается как

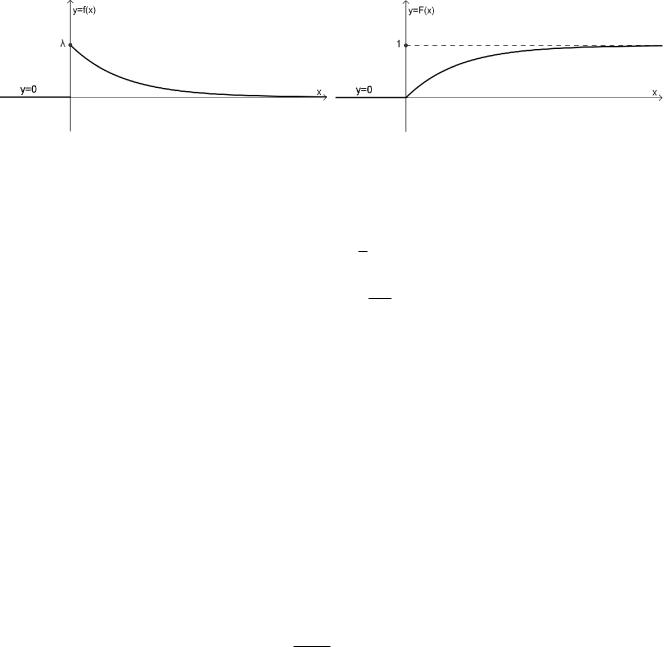
Рис. 5.9: Нормированная функция Лапласа

Для нормального закона N(m, σ) числовые характеристики

MX = m;

41

DX = σ2.

Таким образом, здесь параметр m является математическим ожиданием, а параметр σ

-средним квадратическим отклонением нормальной случайной величины X.

Всилу симметрии графика плотности относительно прямой x = m имеем:

Mo = Me = m.

Нормальный закон широко распространен в природе. Им описываются ошибки измерений, координаты точки попадания снаряда, величина шума в радиоприемном устройстве, линейные размеры и параметры деталей при массовом производстве и т.д.

Для нормального распределения N(m, σ) справедлива формула

P (|X − m| < λm) = 2Φ(λ).

При частных значениях λ из этой формулы находим

P (|X − m| < σ) = 2Φ(1) ≈ 0, 6827;

P (|X − m| < 2σ) = 2Φ(2) ≈ 0, 9545;

P (|X − m| < 3σ) = 2Φ(3) ≈ 0, 9973.

Эти результаты означают, что 99,73% значений случайной величины попадают в промежуток (m − 3σ, m + 3σ), т.е. в этот интервал попадает практически 100% значений случайной величины.

Правило трех сигм. Практически достоверно, что все значения нормальной случайной величины находятся в промежутке (m − 3σ, m + 3σ), т.е. отстоят от центра не более чем на 3σ.

Для сравнения распределений, близких к нормальному N(m, σ), вводится числовая характеристика, называемая эксцесс.

µ4

eX = σ4 − 3.

Здесь µ4 - четвертый центральный момент

+∞

Z

µ4 = (x − mX )4f(x)dx.

−∞

Для нормального распределения eX = 0.

Пусть сравниваемое с нормальным N(m, σ) распределение - симметричное, одномодальное, имеет те же математическое ожидание m и дисперсию σ2 и, кроме того, визуально является близким к нормальному. Тогда можно утверждать, что, если eX > 0, то вершина сравниваемой кривой плотности лежит выше вершины нормальной кривой; если же eX < 0, то ниже.

В силу этого свойства эксцесс называется показателем «островершинности» кривой плотности в сравнении с соответствующей нормальной кривой.

По близости асимметрии aX и эксцесса eX к нулю для произвольного распределения можно сделать вывод о некоторой близости его к нормальному распределению.

42

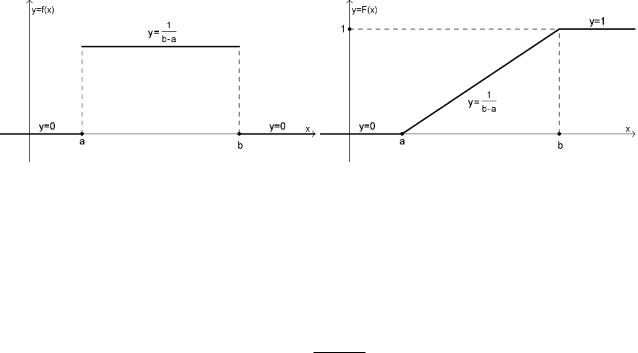
Рис. 5.11: Графики плотности f(x) и функции распределения F (x) для равномерного закона на отрезке [a, b]

Числовые характеристики равномерного распределения на [a, b]:

DX = (b − a)2 .

12

Равномерное распределение применяется для описания ошибок округления, ошибок отсчета по приборам стрелочного типа.

Равномерное распределение на отрезке [0, 1] является стандартным. Оно заложено в микрокалькуляторах, которые производят псевдослучайные числа. Имеются методы, позволяющие преобразовать равномерный закон распределения в другие законы.

44