5.5Непрерывная случайная величина

Пусть некоторая случайная величина имеет бесконечное несчетное множество значений (интервал или объединение интервалов). Дадим определение непрерывной случайной величины.

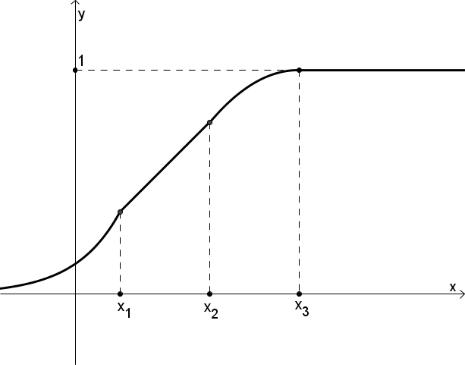
Определение. Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

Отметим, что функция распределения непрерывной случайной величины должна обладать характеристическими свойствами.

Рис. 5.4: График функции распределения непрерывной случайной величины

Непрерывные случайные величины обладают следующим свойством: вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.

На первый взгляд это утверждение может показаться неверным, поскольку вероятность P (α ≤ X ≤ β) складывается из вероятностей попадания случайной величины X в каждую из точек отрезка. Однако теорема сложения вероятностей действует только в случае конечного или счетного множества слагаемых и не работает в случае несчетного множества.

На основании данного утверждения можно сформулировать следующее утверждение: Если X - непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x1, x2) не зависит от того, является ли этот интервал открытым или

закрытым, т.е.

P (x1 < X < x2) = P (x1 ≤ X ≤ x2) = P (x1 < X ≤ x2) = P (x1 ≤ X < x2).

Задание непрерывной случайной величины с помощью функции распределения не является единственным. Введем понятие плотности вероятности непрерывной случайной

36

величины.

Рассмотрим вероятность попадания случайной величины на интервал [x; x + x]. Эта вероятность равна

P (x ≤ X ≤ x + x) = F (x + x) − F (x),

т.е. равна приращению функции распределения F (x) на этом участке. Тогда вероятность, приходящаяся на единицу длины, т.е. средняя плотность вероятности на участке от x до x + x равна

Переходя к пределу при x → 0 в последнем равенстве, получим плотность вероятно-

представляющую производную функции F (x).

Определение. Плотностью вероятности непрерывной случайной величины X называется производная ее функции распределения.

Обозначается плотность вероятности f(x) или ϕ(x). По определению

f(x) = F 0(x).

Плотность вероятности, как и функция распределения, является одной из форм закона распределения непрерывной случайной величины, но в отличие от функции распределения, существует только для непрерывных случайных величин.

Свойства плотности вероятности непрерывной случайной величины.

1. Плотность вероятности - неотрицательная функция, на всей области определения

f(x) ≥ 0.

2.Вероятность попадания непрерывной случайной величины в интервал [a, b] равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.

Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [a, b].

3.Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

x

Z

F (x) = f(t)dt.

−∞

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки x.

37

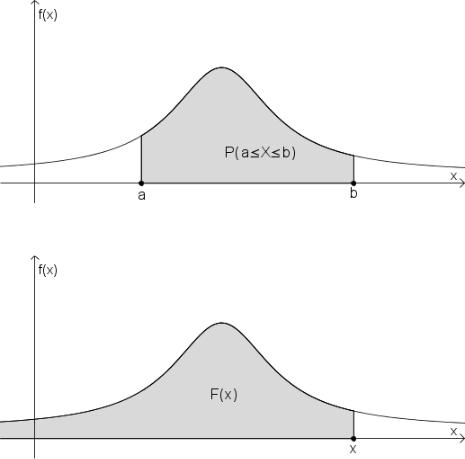
Рис. 5.5: Вероятность попадания в интервал

Рис. 5.6: Геометрическая иллюстрация функции распределения

4.Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

+∞

Z

f(x)dx = 1.

−∞

Геометрически это свойство означает, что полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

5.6Числовые характеристики непрерывной случайной величины

Определение. Математическим ожиданием непрерывной случайной величины X назы-

вается интеграл

+∞

38

Этот интеграл предполагается абсолютно сходящимся. В противном случае, т.е. когда интеграл расходится или сходится условно, считают, что случайная величина X не имеет математического ожидания.

Вероятностный смысл этой формулы такой же, что и для дискретной случайной величины. Это ее среднее значение, точнее - средневзвешенное значение с весовой функцией, равной плотности вероятности.

Математическое ожидание непрерывной случайной величины обладает теми же свойствами, что и математическое ожидание дискретной случайной величины.

Определение дисперсии случайной величины X, данное ранее с помощью формулы

является общим как для дискретной, так и для непрерывной случайной величины. По

этой формуле имеем

+∞

Z

DX = (x − mX )2f(x)dx.

−∞

Свойства дисперсии, сформулированные для дискретных случайных величин, сохраняются и для случая непрерывных случайных величин.

Определение. Модой непрерывной случайной величины называется точка максимума ее плотности вероятности.

Определение. Медианой (Me X, Me) непрерывной случайной величины называется ее значение, обладающее свойством - вероятности попадания случайной величины X левее и правее медианы равны:

P (X < Me) = P (X > Me).

С помощью функции распределения данное равенство записывается в виде F (Me) = 1 − F (Me) откуда

F (Me) = 1/2.

Если F (x) строго возрастает, то медиана единственна. В случае отсутствия математического ожидания его роль, как среднего, обычно выполняет медиана.

Определение. Коэффициентом асимметрии распределения (скошенности), или просто асимметрией называется число, равное отношению третьего центрального момента случайной величины к кубу ее среднего квадратического отклонения:

aX = µ3/σX3 .

Для непрерывной случайной величины aX > 0, если график одномодальной плотности имеет пологую часть справа, а крутую слева от моды; aX < 0, если наоборот; aX = 0 для симметричного распределения.

Определение. Квантилем порядка p непрерывной случайной величины X называется ее значение xp, удовлетворяющее уравнению

F (xp) = p.

Квантили порядков p = 1/4 и p = 3/4 называются соответственно нижней и верхней квартилями.

Если F (x) строго возрастает, то квантиль xp единственна. Квантиль порядка p = 1/2 есть медиана распределения.

39