2.2.2. Аналітичні форми рівнянь регресії

В економетричному моделюванні часто і обґрунтовано застосовують лінійні форми рівнянь регресії як парні (прості),

, (2.1.2)

так і багатофакторні

. (2.1.3)

У цих рівняннях, як ми вже знаємо, параметр означає величинуу, яка не залежить від варіації незалежних змінних 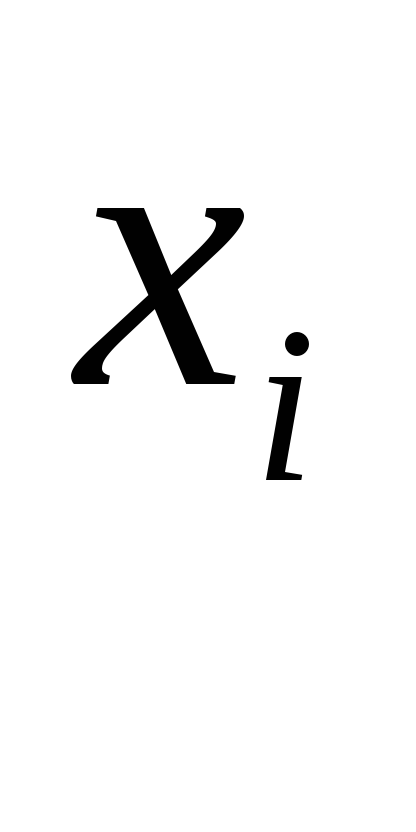і обумовлюється іншими факторами. Його називають у парній регресії перетином. Параметривизначають змінуу при зміні 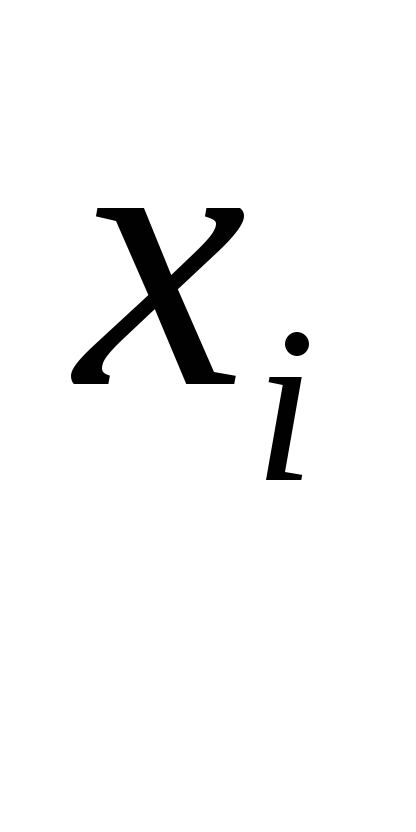на одну одиницю. У парній регресії його називають нахилом (див. рис. 2.3).

Рис. 2.3 − Параметри парної лінійної регресії

Дійсно, – це відрізок до точки перетину лінії регресії з віссюу , а - тангенс кута нахилу лінії регресії до вісіх. У множинній регресії такі назви параметрів (перетин, нахил) не прийнятні, бо в даному разі ми маємо не площину, а багатовимірний простір.

Розрізняють два види (класи) нелінійних регресій. До першого належать регресії, що нелінійні за факторами 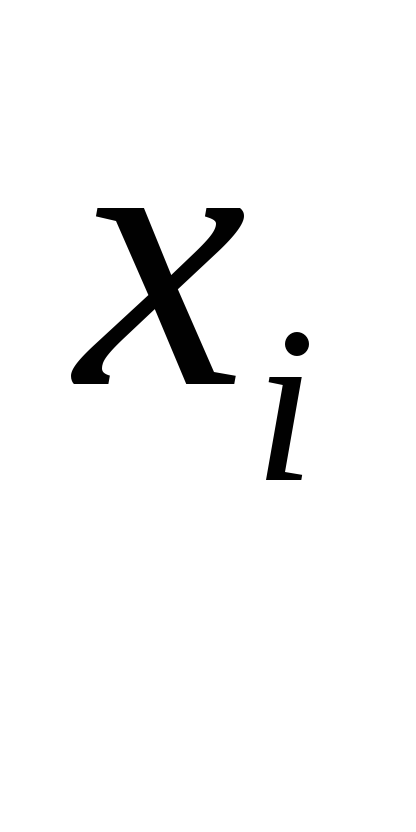, але лінійні відносно параметрів, які підлягають оцінюванню. Такі регресії називаютьсяквазілінійними. До квазілінійних регресій відносяться, наприклад, параболічні другого порядку (квадратичні)

(2.14)

і гіперболічні (зворотні)

. (2.15)

За допомогою парної регресії квадратичної форми можна апроксиміювати прискорене або уповільнене зростання, а також прискорене або уповільнене падіння у при збільшенні х. Парабола другого порядку має вершину, тобто точку насичення зростання або падіння, після якої тенденція зміни у змінюється на симетрично протилежну. Парабола третього порядку має S – подібну форму з двома точками насичення.

Парна гіперболічна регресія придатна для апроксиміювання уповільненого падіння у при зростанні х і має лінію насичення .

Другий клас нелінійних регресій складають суттєво нелінійні регресії, що характеризуються нелінійністю за своїми параметрами. До них належать часто використовувані степенева

; (2.16)

і показникова форми

; . (2.17)

Парні степеневі й показникові форми регресії придатні для апроксиміювання прискореного або уповільненого зростання, а також прискореного або уповільненого падіння залежної змінної, але ці тенденції не обмежені, як у параболи другого порядку, насичення відсутнє.

В окремих випадках застосовують більш складні форми суттєво нелінійної регресії:

• модифікована експонента

, (2.18)

• крива Гомперця

, (2.19)

• логістична крива (крива Перла-Ріда)

. (2.20)

У цих формах і– невідомі параметри рівняння регресії, що підлягають оцінюванню.

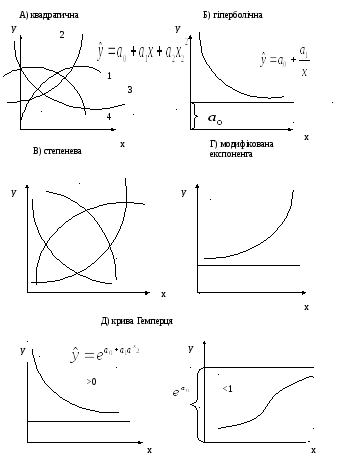
На рис. 2.4 наведені приклади графіків криволінійних форм парної регресії (для >0;x>0):

1/2 а₀

Рис. 2.4 − Графіки квазілінійних і суттєво нелінійних форм залежностей