2.1.3. Тестування суттєвості (невипадковості) коефіцієнтів кореляції

Оскільки коефіцієнт кореляції визначається за вибірковою сукупністю об’єктів спостереження, необхідно оцінювати його значущість і будувати інтервали довіри для істинного коефіцієнта кореляції в генеральній сукупності об’єктів.

Значущість коефіцієнта кореляції перевіряють за допомогою t – статистики, яка має розподіл Стьюдента з (п-2) ступенями свободи. Величину t визначають за формулою

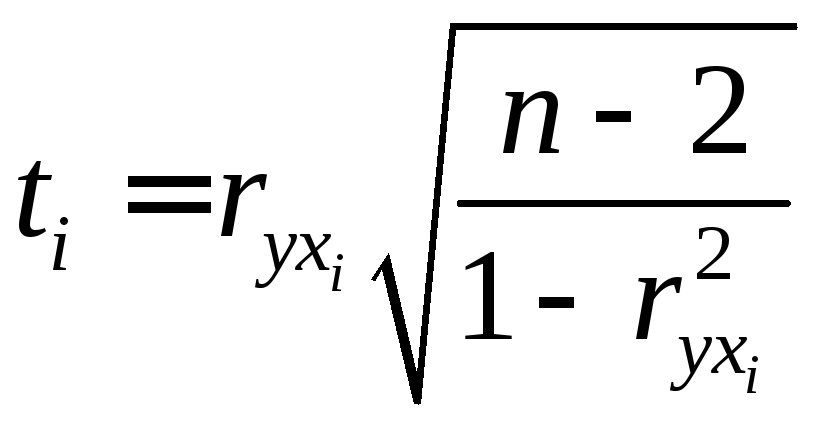(2.3)

і співставляють з критичним значенням за t –критерієм Стьюдента (див. додаток 3). Якщо >, то з ймовірністю 0,95 і більше можна стверджувати, що коефіцієнт кореляції значущий (не дорівнює 0) і зв‘язок між іє суттєвим, невипадковим.

Визначимо t –статистики для нашого прикладу:

;

.

За додатком 3 при n-m-1=29-1-1=27 i Р=0,95, критичне значення t становить 2,052. Оскільки 10,61>2,052 і 5,92>2,052, робимо висновок, що обидва фактори значущо і достатньо сильно впливають на рентабельність витрат і що цей вплив невипадковий.

2.1.4. Інтервали довіри для коефіцієнтів кореляції

Очевидно, що вибірковий коефіцієнт кореляції як випадкова величина має асиметричний розподіл (особливо при малих вибірках і великих за модулем значеннях). Це неважко зрозуміти, коли уявити, що, наприклад, при =0,8 вибіркові коефіцієнти в інших вибірках можуть перебільшити цю величину тільки на 0,2, тоді як у бік зменшення вони можуть знаходитись від неї на 0,8. Доведено, що при збільшенні об‘єму вибірки ця асиметрія зменшується. Як же побудуватиінтервали довіри (довірчі границі) для коефіцієнта кореляції?

Зручний підхід для розв‘язання цієї задачі запропонував в 1921 р. Р.Фішер. Він сконструював перетворення випадкової величини у випадкову величинуz:

, (2.4)

яка розподілена майже за нормальним законом (симетрично) з середнім квадратичним відхиленням

.

Отже для випадкової величини z, як і для будь − якої нормально розподіленої величини, гранична помилка вибірки з ймовірністю 0,95 не перевищить

. (2.5)

Знайдемо нижню і верхню границі інтервалу довіри для z, тобто

і ,

а потім і границі довіри для коефіцієнта кореляції. Для цього можна скористатися спеціальною таблицею z – перетворення Р.Фішера (додаток 4).

Побудуємо інтервали довіри для коефіцієнтів кореляції в нашому прикладі. Нагадаємо, що r_РЕ=0,8981; r_РК=0,7513; n=29. За формулою (3.4) знаходимо

,

і визначаємо за формулою (2.5) нижні й верхні границі інтервалів довіри для z.

нижня верхня

для Z_E

для Z_K

Тепер за таблицею Z-перетворення Р.Фішера (додаток 4) по знаходимо довірчі границі для теоретичних коефіцієнтів кореляції ():

0,79 ≤≤0,95;

0,53 ≤≤0,88.

Звернемо увагу, що одержані границі (0,79-0,95) і (0,53 – 0,88) не знаходяться на однаковій відстані від вибіркових значень коефіцієнтів кореляції 0,90 і 0,75, що свідчить про асиметричний розподіл вибіркових коефіцієнтів кореляції.

На закінчення розгляду питання про оцінки значущості й інтервалів довіри для коефіцієнтів кореляції додатково зауважимо наступне:

1) якщо коефіцієнт кореляції від’ємний, то в розрахунках (див. формулу (2.3) ніяких особливостей або ускладнень не виникає, але в розрахунках(формула 2.4) коефіцієнт кореляції треба приймати за модулем;

2) якщо коефіцієнт кореляції має невелике значення, наприклад, 0,25, тоді за формулою (2.4) z=0,255, (за формулою (2.5)=0,384 і нижня границя інтервалу довіри дляz набуває від‘ємного значення: -0,129 (0,255-0,384). Це означає, що і інтервал довіри для також включає значення 0. Така незалежна змінна, безумовно, є незначущою і її напевно слід вилучити з подальшого процесу моделювання.