2.1.10. Вилучення екзогенних змінних

Рішення щодо включення незалежних змінних (факторів) у рівняння регресії приймається за наслідками тестування на значущість (невипадковість) їхнього впливу на залежну змінну за t – статистикою Стьюдента, автономність впливу за - тестом і достатність вкладу у множинний коефіцієнт детермінації за- тестом. Для зручності визначення складають зведення результатів тестування. Для нашого прикладу таке зведення представлене у табл. 2.2.

Таблиця 2.2 − Зведення результатів тестування факторів

Фактори	t–статистика Стьюдента (2,052)	- тест (0)	- тест ()
Е	10,61	0,775	2,277
К	5,92	0,468	1,148

Фактор енергоозброєності праці (Е) за всіма тестами безумовно включається до рівняння регресії. Фактор постійності ПВП (К) помітно слабкіший, але з деяким сумнівом відносно його вагомості у множинному коефіцієнті детермінації також можна ввести в рівняння регресії.

Такі рішення, як правило, остаточні, хоча на стадії оцінювання параметрів рівняння регресії іноді трапляються випадки вилучення факторів.

2.2. Специфікація аналітичної форми рівнянь регресії

2.2.1. Мета і способи специфікації

Парні й багатофакторні лінійні економетричні моделі, які часто використовуються в економіці, не завжди відображають дійсні закономірності розвитку і зв’язків між соціально-економічними явищами і процесами. Тому на практиці для побудови адекватних економетричних моделей застосовують нелінійні форми рівнянь регресії.

Нелінійні форми рівнянь регресії використовують з метою, по-перше, максимально апроксиміювати сутність явища за економічною теорією і, по-друге, максимально зменшити помилку оцінювання параметрів і прогнозу залежної змінної.

Наведемо приклади апріорі криволінійних форм регресії. З ростом доходу, наприклад, сім’ї обсяг її споживання зростає. За економічною теорією це зростання необмежене, але воно має монотонно уповільнений характер. Отже зростання споживання описується кривою лінією зростання з від‘ємним прискоренням. Другий приклад: собівартість одиниці продукції за рахунок збільшення обсягу її виробництва знижується, але за теорією це зниження не може бути лінійним. Воно має обмеження – величину постійних витрат на одиницю продукції. Отже ця залежність криволінійна. Очевидно, в економетричних моделях теоретично вірні уяви про форми залежностей повинні лежати в основі форми регресії.

Застосування криволінійних форм регресії, має і суто прагматичну мету – одержання ефективних оцінок параметрів рівняння регресії, тобто зменшення залишкової дисперсії, що не пояснюється рівнянням регресії. На рис. 2.2 наведене поле кореляції і дві форми рівняння регресії: 1) лінійна () і 2)степенева (). Залишки (відхилення точок поля від лінії регресії) при лінійній формі набагато більші, ніж при степеневій. Відповідно і оцінка параметрівіу степеневій формі рівняння регресії набагато ефективніша, прогноз залежної змінної в даному разі набагато точніший.

е

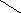
Рис. 2.2 − Лінійна і степенева форми регресії

Способи специфікації (обґрунтування) форми рівняння регресії такі : теоретичний, графічний, аналітичний і сигмальний.

Теоретичний спосіб обґрунтування форми рівняння регресії базується на економіко-теоритичному аналізі сутності явища, що моделюється, із застосуванням професійних знань. Цей спосіб безпомилковий, найкращий, але він вимагає від аналітика високої професійної підготовки і розвинутого економічного мислення.

Графічний спосіб специфікації заснований на візуальному аналізі полів кореляції. Цей спосіб доступний для будь-кого: розглядай поля кореляції і підбирай найбільш адекватну форму рівняння регресії «на око». Дуже просто, але не завжди ефективно. Тому графічний спосіб можна рекомендувати як допоміжний до теоретичного.

Аналітичні способи багаточисельні. Один з них (спосіб перших різниць) ми розглянемо далі.

Сигмальний спосіб полягає в тому, що форма рівняння регресії взагалі спеціально не обґрунтовується, а вибирається з декількох варіантів. Це ефективний спосіб, але він трудомісткий. Приймаються кілька варіантів форми рівняння регресії, для кожного з них оцінюються параметри регресії і розраховується залишкова дисперсія. Той варіант специфікації, який забезпечує мінімальну дисперсію залишків (), вибирається як остаточний.