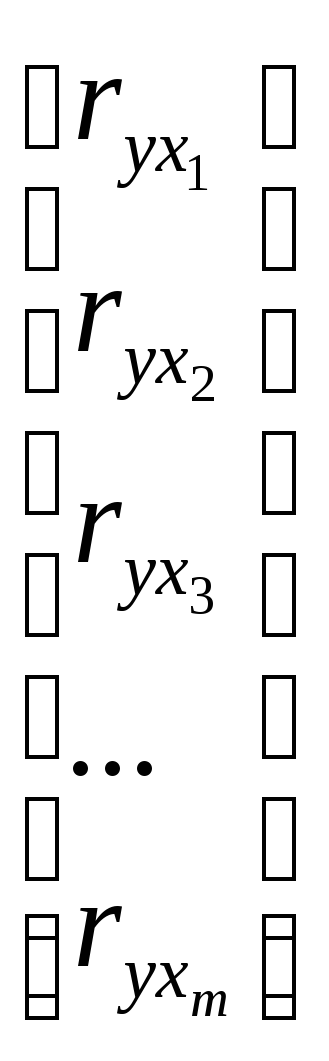- •Економетрія
- •Змістовий модуль 1: постановка задачі економетричного моделювання
- •1.1. Предмет, заВдання і зміст економетричного моделювання
- •1.1.1. Предмет економетрії
- •1.1.2. Проблеми і завдання економетричного моделювання
- •1.1.3. Зміст (послідовність) економетричного моделювання
- •1.2. Формування матриці даних для економетричного моделювання
- •1.2.1 Загальна характеристика матриці
- •1.2.2 Змінні в матриці
- •1.2.3. Об’єкти спостереження в матриці
- •1.2.4. Вимоги до розмірів матриці
- •1.2.5. Показники варіації змінних
- •1.2.6. Поля кореляції і їх аналіз
- •1.2.7. Вилучення аномальних об’єктів спостереження
- •1.3. Комплекс контрольних завдань
- •Навчальні елементи, що підлягають контролю і оцінюванню:
- •1.3.1. Тестові завдання
- •1.3.2. Логічні вправи
- •1.3.3. Розрахункові вправи
- •Змістовий модуль 2: специфікація економетричних моделей
- •2.1. Ідентифікація незалежних змінних
- •2.1.1. Мета і послідовність ідентифікації
- •2.1.2. Коефіцієнти парної кореляції і детермінації
- •2.1.3. Тестування суттєвості (невипадковості) коефіцієнтів кореляції
- •2.1.4. Інтервали довіри для коефіцієнтів кореляції
- •2.1.5 Мультиколінеарність
- •2.1.6. Бета - коефіцієнти
- •2.1.7. Тестування автономії екзогенних змінних
- •2.1.8. Коефіцієнт множинної кореляції і детермінації
- •2.1.9. Тестування значущості вкладу факторів у множинну детермінацію
- •2.1.10. Вилучення екзогенних змінних
- •2.2. Специфікація аналітичної форми рівнянь регресії
- •2.2.1. Мета і способи специфікації
- •2.2.2. Аналітичні форми рівнянь регресії
- •2.2.3. Спосіб перших різниць
- •2.2.4. Лінеаризація нелінійних рівнянь регресії
- •2.3. Комплекс контрольних завдань
- •Навчальні елементи, що підлягають контролю і оцінюванню:
- •2.3.1. Тестові завдання
- •2.3.2. Логічні вправи
- •2.3.3. Розрахункові вправи
- •Змістовий модуль 3: оцінювання параметрів економетричних моделей
- •3.1. Оцінювання параметрів рівнянь регресії
- •3.1.1. Мета і вимоги до оцінювання параметрів
- •3.1.2. Основні припущення щодо оцінювання параметрів
- •3.1.3. Метод найменших квадратів
- •3.1.4. Виконання за мнк основних припущень щодо оцінювання параметрів
- •3.1.5. Гетероскедастичність
- •3.1.6. Автокореляція
- •3.1.7. Значущість (адекватність) рівняння регресії
- •3.1.8. Перевірка значущості параметрів моделі
- •3.1.9. Інтервали довіри до коефіцієнтів регресії
- •3.2. Прогнозування залежної змінної
- •3.2.1. Прогнозування на парних моделях
- •3.2.2. Прогнозування на множинних моделях
- •3.3. Комплекс контрольних завдань
- •Навчальні елементи, що підлягають контролю і оцінюванню:
- •3.3.1. Тестові завдання
- •3.3.2. Логічні вправи
- •3.3.3. Розрахункові вправи
- •4. Відповіді до розрахункових вправ
- •Економетричних моделей
- •Список літератури
- •Критичні значення t для побудови прямокутного шаблону двомірного розсіювання*
- •Значення f – критерію Фішера
- •Навчальне видання
- •61002, Харків, хнамг, вул. Революції, 12
- •61002, Харків, хнамг, вул. Революції, 12
2.1.5 Мультиколінеарність
Термін
«мультиколінеарність»
вперше ввів Р. Фріш (1934р.). За Фрішем
мультиколінеарність означає, що в
багатофакторній регресійній моделі
дві або більше, навіть всі незалежні
змінні (фактори) зв‘язані між собою і
мають певний ступінь кореляції (![]() ≠0,
і ≠
j
).
Це наслідок глобальної тенденції
одночасної зміни економічних показників.
В економіці взагалі важко уявити
відсутність кореляції, її наявність
об‘єктивна.
≠0,
і ≠
j
).
Це наслідок глобальної тенденції
одночасної зміни економічних показників.
В економіці взагалі важко уявити
відсутність кореляції, її наявність
об‘єктивна.
У нашому прикладі кореляція між енергоозброєністю праці і коефіцієнтом постійності ПВП складає (див. табл. 1.5 і 2.1):
 ,
,
що свідчить про більш ніж помірну колінеарність цих двох факторів.
Чому
наявність мультиколінеарності є
проблемою, які негативні наслідки в
економетричному моделюванні вона
породжує? Відповідь проста:
мультиколінеарність не дозволяє
обґрунтовано оцінити параметри рівняння
регресії, помилки цих оцінок великі.
При наявності сильної мультиколінеарності
(![]()
![]() 1,і
≠
j)
може статися, що не тільки абсолютні
величини коефіцієнтів регресії оцінені
неправильно , а і їх знаки.
1,і
≠
j)
може статися, що не тільки абсолютні
величини коефіцієнтів регресії оцінені
неправильно , а і їх знаки.
Тестування наявності і визначення сили мультиколінеарності не має єдиного підходу. Тому наведемо кілька простих методів тестування.
Мультиколінеарність наявна, якщо сума парних коефіцієнтів детермінації перевищує 1, тобто
![]() >1.
>1.
У нашому
прикладі саме це і спостерігається
![]() .
Це означає, що оцінки
.
Це означає, що оцінки![]() і
і![]() завищені саме через колінеарність цих
факторів.
завищені саме через колінеарність цих
факторів.
Чим
більше
![]() перевищує одиницю, тим більше сила
мультиколінеарності, тому що за
відсутності мультиколінеарності
перевищує одиницю, тим більше сила
мультиколінеарності, тому що за
відсутності мультиколінеарності
![]()
![]() <1.
<1.
Поширеним тестом на наявність мультиколінеарності є великі величини коефіцієнтів кореляції між окремими парами змінних. Якщо значення хоча б одного коефіцієнта кореляції більше 0,8, то мультиколінеарність є серйозною проблемою. Але недоліком цього тесту є те, що високе значення парних коефіцієнтів кореляції – необхідна, але не достатня умова наявності мультиколінеарності.
Для визначення наявності й сили (рівня) колінеарності можна застосувати порівняння коефіцієнтів взаємної кореляції (
 )
з коефіцієнтами кореляції залежної
змінної з факторами (
)
з коефіцієнтами кореляції залежної
змінної з факторами ( ):
):
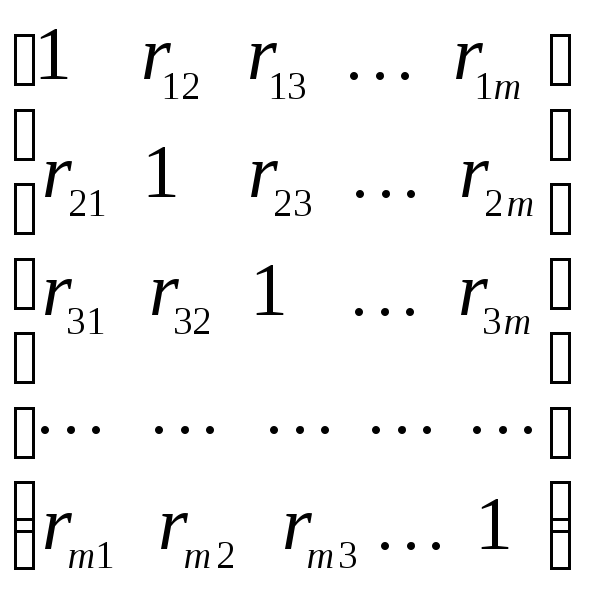
|
матриця
коефіцієнтів взаємної кореляції
|
вектор
коефіцієнтів кореляції
|
|
|
|
Тести такі:
якщо
 ≠0,
мультиколінеарність наявна;
≠0,
мультиколінеарність наявна;якщо всі
 <
<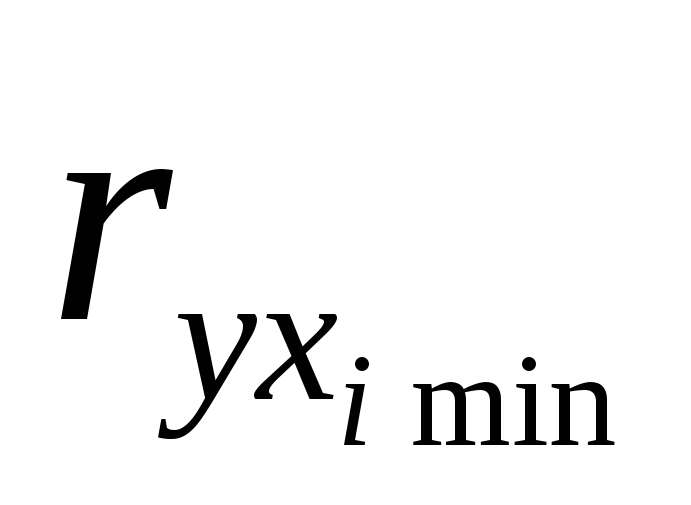 ,
мультиколінеарність є , але вона слабка;
,
мультиколінеарність є , але вона слабка;якщо всі
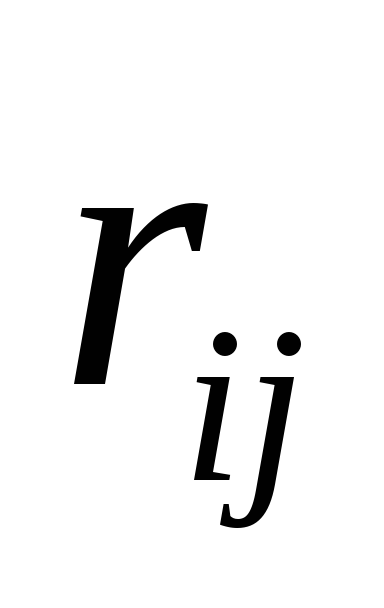 знаходяться в межах від
знаходяться в межах від до
до ,
мультиколінеарність помірна;
,
мультиколінеарність помірна;якщо хоча б один
 >
> ,
мультиколінеарність
сильна.
,
мультиколінеарність
сильна.
У нашому прикладі з двома незалежними змінними це порівняння полягає в співставленні двох матриць



Мультиколінеарність,
як бачимо, наявна, оскільки![]() .
Але її сила або рівень невисокий, слабкий,
тому що 0,5774<
0,8981 і 0,7513.
.
Але її сила або рівень невисокий, слабкий,
тому що 0,5774<
0,8981 і 0,7513.
Що робити, коли мультиколінеарність виявлено? Безпомилкових порад немає, оскільки вона є прикладною проблемою. Можна запропонувати декілька простих методів вилучення явища мультиколінеарності, принаймні зниження її рівня:
перетворення незалежних змінних;
вилучення незалежних змінних;
тестування незалежних змінних на автономність.
Перетворення
незалежних змінних
полягає,
наприклад, в заміні якоїсь із сильно
корельованих змінних
![]() на
на![]() ,
заміні абсолютних значень
,
заміні абсолютних значень![]() відносними величинами, заміні операційної
характеристики змінної
відносними величинами, заміні операційної
характеристики змінної![]() іншою і т.п. Це може привести до послаблення
мультиколеніарності факторів.
іншою і т.п. Це може привести до послаблення
мультиколеніарності факторів.
Вилучення
незалежних змінних як
засіб вилучення або послаблення
мультиколеніарності полягає в тому, що
з двох змінних з високою коленіарністю
(![]()
![]() 1)
вилучають ту, яка має менший коефіцієнт
кореляції із залежною змінною (
1)
вилучають ту, яка має менший коефіцієнт
кореляції із залежною змінною (![]() ).
Але вилучення незалежної змінної з
моделі може призводити до помилки
ідентифікації. Так, за економічною
теорією, для моделювання залежності
споживання необхідно включати фактори
доходу і багатства, але доход і багатство
є сильно корельованими факторами. Тоді
вилучення будь-якої з них створюватиме
помилку ідентифікації моделі. У таких
випадках треба шукати інший спосіб
зниження рівня мультиколінеарності.
).
Але вилучення незалежної змінної з
моделі може призводити до помилки
ідентифікації. Так, за економічною
теорією, для моделювання залежності
споживання необхідно включати фактори
доходу і багатства, але доход і багатство
є сильно корельованими факторами. Тоді
вилучення будь-якої з них створюватиме
помилку ідентифікації моделі. У таких
випадках треба шукати інший спосіб
зниження рівня мультиколінеарності.
Сутність методу тестування незалежних змінних на автономність розглянемо в наступному підрозділі.