0

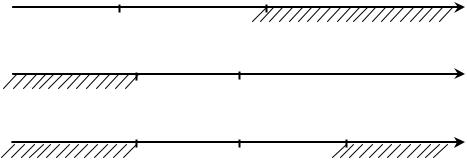
РИС. 12.1.4

Здесь критическая область покрыта штриховкой. Если Kнабл. попадает в крити-

ческую область, то нулевая гипотеза отвергается.

Критерии, служащие для проверки гипотез о распределении генеральной совокупности называются критериями согласия. Критерии, служащие для проверки гипотез о параметрах распределения называются параметрически-

ми.

12.1.2.Контрольные вопросы

Что такое генеральная совокупность и выборка?

Что такое статистический ряд и группированный статистический ряд, какие у них графическое изображения?

Что такое точечные и интервальные оценки?

Что такое статистическая гипотеза, нулевая гипотеза, альтернативная гипотеза, уровень значимости?

12.1.3. Практическое задание для самостоятельной работы

Задача 1. Варианты

1)В некоторый период времени относительная частота солнечных дней составила 0,6. Сколько дней было пасмурных, если солнечных дней было 42?

2)Относительная частота попадания у данного стрелка оказалась равной 0,9. Сколько он произвел выстрелов, если промахнулся 9 раз?

3)Через остановку проходят автобусы маршрутов №2,5,6,8,20. Пассажира устраивают маршруты №5 и №8. Определить вероятность того, что первый по-

дошедший к остановке автобус будет нужного маршрута, если известно, что

152

второго маршрута 8 машин, пятого – 15, шестого – 12, восьмого – 10, двадцато-

го – 5.

4)В ящике 50 одинаковых жетонов, помещенных номерами от 1 до 50. определить вероятность того, что наудачу вынутый жетон окажется с номером, сумма цифр которого окажется 7, либо 9, либо 11.

5)Вероятности пятилетней службы каждой из трех деталей механизма равны 0,5; 0,6; 0,7. Определить вероятность того, что механизм в целом прослужит пять лет.

6)Для одного рабочего вероятность выполнить норму выработки равна 0,9, для другого – 0,85. Определить вероятность того, что оба рабочих не выполнят норму выработки.

7)Рабочий за смену изготовил 15 деталей высшего и 6 деталей высшего сорта. Случайным образом последовательно извлекаются две детали. Найти вероятность:

- что обе детали окажутся первого сорта; - одна деталь высшего сорта, другая первого сорта.

8)Из трамвайного парка в случайном порядке последовательно выходят 3 трамвая маршрута №1 и 4 трамвая маршрута №2. Определить вероятность того, что вторым по порядку выйдет трамвай маршрута №2.

9)Два игрока бросают по одному игральному кубику. Определить вероятность того, что хотя бы на одном из кубиков выпадет число очков, кратное трем.

10)Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить три бомбы, вероятности попаданий которых соответственно равны 0,3; 0,4; 0,6.

11)Сколько раз нужно подбросить монету, чтобы с вероятностью 0,9375 можно было утверждать, что хотя бы один раз выпадет герб?

153

12)В начале учебного года в группе по списку было 30 студентов. Из них 20 получили стипендию. В середине семестра один студент взял академический отпуск. Определить вероятность того, что случайно отобранный после этого студент окажется стипендиатом.

13)В ящике содержится 12 деталей завода №1, 20 деталей завода №2 и 18 деталей завода №3. Вероятность того, что деталь завода №1 отличного качества равна 0,9; для деталей завода №2 и №3 эти вероятности, соответственно, равны 0,6 и 0,9. Определить вероятность того, что наудачу извлеченная деталь окажется отличного качества.

14)На склад готовой продукции поступили изделия из трех цехов: 30% - из первого, 45% - из второго и 25% - из третьего. Среди изделий первого цеха брак составляет в среднем 0,6%, второго – 0,4% и третьего – 0,16%. Определить вероятность того, что взятое наудачу на складе изделие окажется годным.

15)В группе 25 студентов, из них десять – выпускники вечерней школы, а остальные окончили среднюю школу. Вероятность успешной сдачи экзамена по статистики выпускником вечерней школы равна 0,8, а выпускником средней школы – 0,9. Наудачу вызванный студент сдал экзамен успешно. Определить вероятность того, что это выпускник вечерней школы.

16)В железнодорожном составе 50 вагонов, груженных углем двух сортов, в том числе 25 вагонов содержат 70% угля первого сорта; 15 вагонов содержат 60% и 10 вагонов – 85% угля второго сорта. Случайно взятый для анализа кусок оказался второго сорта. Определить вероятность того, что он взят из вагона первой группы.

17)На двух станках производятся одинаковые детали. Вероятность того, что деталь первого станка стандартна, равна 0,9, второго 0,8. Производительность первого станка вдвое больше производительность второго. Деталь взятая наудачу с транспортера, на который сбрасываются детали с обоих станков, оказалась стандартной. Определить вероятность того, что деталь изготовлена на первом станке.

154

Задача 2. Варианты

1)Вероятность того, что из двух приобретенных билетов оба окажутся выигрышными рана 0,49. Определить вероятность того, что из шести билетов выиграют три.

2)Вероятность прокола колеса автомобиля при поездке равна 0,1. На сколько вероятнее доехать до конечного пункта следования с запасным колесом, чем без запасного колеса?

3)Игральная кость бросается 120 раз. Определить наивероятнейшее число выпадений шести очков на верхней грани кости.

4)На складе находится продукция двух цехов, причем в продукции плюс первого цеха содержится 60 % изделий высшего сорта, в продукции второго цеха – 70%. Для контроля качества продукции берутся 50 продукций первого цеха и 40 изделий второго цеха. Определить, в продукции какого цеха наивероятнейшее число изделий высшего сорта окажется наибольшим.

5)В зимнее время вероятность своевременного прибытия поезда на станцию принимается равным 0,8. Определить вероятность того, что из 30 ожидаемых поездов 25 прибудут своевременно.

6)На факультете института 40% всех студентов занимаются в спортивных секциях. Найти наивероятнейшее число студентов, занимающихся в спортивных секциях, их 250 студентов и вероятность того, что именно это число студентов занимается в спортивных секциях.

7)Школьники посадили на своем участке 500 деревьев. Вероятность того, что дерево приживется равна 0,6. Определить вероятность того, что число прижившихся деревьев окажется в пределах от 278 до333.

8)Известно, что для присуждения спортивных разрядов по стрельбе необходимо набрать хотя бы 90 очков из 100 возможных. Определить вероятность того, что стрелок станет разрядником, если для него вероятность попадания в цель при каждом выстреле равна 0,8.

155

9)При массовом выпуске некоторой продукции бывает в среднем 4 % брака. Определить вероятность того, что в партии 625 единиц этой продукции отклонение от установленного процента брака по абсолютной величине будет не более чем 0,02.

10)Вероятность безбилетного проезда на транспорте равна 0,05. Обследовано 400 человек. С вероятностью 0,9545 определить:

а)границы изменения относительной частоты безбилетных пассажиров; б)границы, в которых заключено число безбилетных пассажиров среди

обследованных.

11)Всхожесть семян характеризуется вероятностью 0,7. Определить,

сколько нужно посеять семян, чтобы с вероятностью 0,9973 можно было утверждать, что частность проросших семян будет отличатся от 0,7 по абсолютной величине не более, чем на 0,02.

Задача 3. Варианты

1)Вероятность возникновения погрешности при изменении равна 0,2. Проведено три измерения. Составить закон распределения случайной величины

–числа измерений произведенных без погрешности. Вычислить числовые характеристики: математическое ожидание М(Х), дисперсию D(Х).

2)Прибор укомплектовывается тремя однотипными блоками. Контролер проверяет последовательно каждый блок на работоспособность. Как только выявляется неработающий блок, прибор бракуется. Составить закон распределения случайной величины – числа проверяемых блоков приборов, если вероятность появления неисправного блока равна 0,1. Найти числовые характеристи-

ки: М(Х), D(X).

3)Четыре покупателя входят в магазин. Для каждого покупателя вероятность сделать покупку равна 0,6. составить закон распределения случайной величины - числа покупателей, сделавших покупку. Найти числовые характеристики случайной величины: М(Х), D(X).

156

4)На экзамене студенту задаются дополнительные вопросы, но не более трех. Как только студент правильно отвечает на заданный вопрос, экзаменатор прекращает задавать дополнительные вопросы. Вероятность того, что студент правильно ответит на любой заданный вопрос, равна 0,7. Составить закон распределения случайной величины – числа дополнительных вопросов, заданных студенту. Вычислить: М(Х), D(X).

5)Вероятность того, что телевизор не потребует ремонта в течении гарантированного срока равна 0,8. Составить закон распределения случайной величины – числа телевизоров, которые не потребуют гарантированного ремонта, из пяти проданных телевизоров. Найти числовые характеристики М(Х), D(X).

6)Дается пять попыток включить двигатель до первой успешной попытки. Вероятность того, что двигатель включится равна 0,6. Составить закон распределения случайной величины – числа попыток, в результате которых можно запустить двигатель. Найти числовые характеристики: М(Х), D(X).

7)Вероятность того, что из двух, телевизионных камер в данный момент включена одна, равна 0,42. В студии имеются 20 телевизионных камер. Найти вероятность того, что в данный момент включены:

- 18 камер; - хотя бы 15 камер. (вероятность включения каждой из камер больше 0,5) .

8)Один из видов продукции производится на трех фабриках, входящих в состав производственного объединения. Первая фабрика производит 40% всего выпуска продукции, вторая – 35%, третья – 25%. В продукции первой фабрики обнаружено 30% изделий низкого качества, в продукции второй фабрики - 20%,

впродукции третьей фабрики 12%. Какова вероятность того, что среди 500 изделий производственного объединения число изделий высшего качества будет

400 до 410.

9)По данным длительной проверки качества запчастей определенного вида брак составляет 5 %. Изготовлено 500 запчастей. Определить математическое ожидание и дисперсию числа годных запчастей.

157

10) Всхожесть семян некоторого сорта пшеницы составляет 93%. Определить математическое ожидание и дисперсию числа всходов, если высажено 70 семян.

Задача 4. Варианты

1) Случайная величина Х задана интегральной функцией:

Определить:

а) дифференциальную функцию f(х);

б) вероятность того, что Х примет значение, принадлежащее интервалу

(2,5;3,5)

2) Случайная величина Х задана интегральной функцией:

Определить:

а) вероятность того, что Х примет значение, принадлежащее интервалу

(1/2;1);

б) математическое ожидание и дисперсию этой случайной величины. 3) Случайная величина Х задана интегральной функцией:

Определить вероятность того, Х примет значение, принадлежащее интер-

валу (π / 6;π / 4) .

4) Случайная величина Х задана дифференциальной функцией:

158

Определить:

а) коэффициент а; б) математическое ожидание и дисперсию этой случайной величины.

5) Случайная величина задана дифференциальной функцией:

Определить:

а) коэффициент а; б) интегральную функцию;

в) математическое ожидание и дисперсию этой случайной величины. 6) Случайная величина Х задана дифференциальной функцией:

Определить:

а) интегральную функцию; б) математическое ожидание и дисперсию этой случайной величины.

7) Случайная величина Х задана дифференциальной функцией:

а) коэффициент а; б) вероятность того, что случайная величина Х примет значение, принад-

лежащее интервалу (0; π / 2 ); в) математическое ожидание и дисперсию этой величины.

159

8) Случайная величина Х задана интегральной функцией:

(1/2;1);

б) математическое ожидание и дисперсию этой случайной величины. 9) Случайная величина Х задана интегральной функцией:

0, x ≤ 0,

F(x) = x, 0 < x ≤1,1, x >1.

Определить:

а) вероятность того, что Х примет значение, принадлежащее интервалу

(1/2;3/2);

б) математическое ожидание и дисперсию этой случайной величины.

Задача 5. Варианты

1.В магазинах торга выборочным методом был подсчитан средний стаж работы 100 сотрудников. Оказалось, что он равен в среднем 10 годам при среднем квадратичном отклонении 3 года. Определить надежность, с которой можно утверждать, что отклонение полученной выборочной средней от генеральной средней не превысит 1 года

2.Обследуется содержание белка в привезенной на элеватор пшенице. В лабораторию взят для исследования 1 кг (1000 гр) зерен. Доля белка в этих зернах 0,17. С надежностью 0,9545 найти доверительный интервал, в котором заключена доля белка во всей пшенице.

3.Сколько рабочих –сдельщиков можно включить в выборку для определения средней выработки одного рабочего, чтобы предельная ошибка не пре-

160

вышала 2,5 ден. ед. с вероятностью 0,9973 при среднем квадратичном отклонении 15 д.е.

4.Был проведен выборочный опрос 25 студентов о распределении бюджета времени. Обследование показало, что в среднем ежедневные затраты времени на самостоятельную работу составляют 4 часа при среднем квадратичном отклонении 0,5 часа. Определить с вероятностью 0,9973 среднюю и предельную ошибки, а также доверительный интервал, в котором заключена генеральная средняя.

5.Для выявления удельного веса неработающих станков отобрано 100 станков. Неработающих оказалось 20. С надежностью 0,95 оценить доверительный интервал, в котором окажется доля неработающих станков во всей совокупности.

6.Сколько рабочих – сдельщиков можно включить в выборку для определения средней выборки одного рабочего – сдельщика, чтобы предельная ошибка не превышала 2,5 ден. ед., при среднем квадратическом отклонении 15 ден. ед.,..а надежность 0,9973

7.В магазинах коопторга выборочным методом был подсчитан средний стаж работы 100 продавцов. Оказалось, что он равен в среднем 10 годам при среднем квадратическом отклонении 3 года. С какой надежностью можно утверждать, что отклонение полученной выборочной средней от генеральной средней не превысит одного года.

8.Даны результаты обследования 100 взрослых мужчин по росту:

Определить:

1) доверительный интервал, в котором с надежностью 0,9973 заключен средний рост всех мужчин;

161

2) доверительный интервал, в котором с надежностью 0,9545 заключена доля мужчин, имеющих рост 170см и более

9. Результаты выборочного наблюдения за обработкой рабочими одной

1)среднее время обработки одной детали рабочими всего цеха, в котором работают 2000 рабочих;

2)долю рабочих всего цеха, обрабатывающих детали менее чем за 6 ми-

нут.

10.Даны результаты выборочного (бесповторного) обследования заработной платы 100 рабочих предприятия, на котором занято 1000 рабочих:

Определить:

1)доверительный интервал, в котором с надежностью 0,9545 заключена средняя заработная плата всех рабочих предприятия;

2) с вероятностью 0,9973 предельной доли рабочих, имеющих заработную плату менее 2,9 тыс. руб.

11. В результате обследования стажа работы сотрудников предприятия получены следующие данные:

162

Определить: 1) доверительный интервал, в котором с надежностью 0,9973 заключен средний стаж работы сотрудников всего предприятия, на котором занято 1000 человек;

2)доверительный интервал, в котором с надежностью 0,9545 заключена доля сотрудников предприятия, имеющих стаж работы 10 лет и более.

Задача 6. Варианты

1. Для сравнения производительности труда рабочих двух цехов экономист исследовал среднюю выработку рабочих. Обследовано n1= 40 рабочих в первом цехе и n2 = 38 во второй. Выборочные средние х1 =142 д.е., х2 =145 д.е.

Генеральные дисперсии Д(х1 ) = 2,4 Д(х2 ) = 2,8 При уровне значимости α = 0,1

проверить нулевую гипотезу Н0 : х1 = х2 при конкурирующей гипотезе Н1 :

х1 ≠ х2 Можно ли считать, что рабочие обоих цехов имеют одинаковую произ-

водительность?

2. Стандартный срок службы электроприбора а = 1000 часов. Проверка 50 приборов показала, что средний срок службы х = 970 часов, при среднем квадратическом отклонении σ0 (х) = 30 часов. При уровне значимости α = 0,01 про-

верить нулевую гипотезу Н0: х = а если конкурирующая гипотеза Н1: х < a . Удовлетворяет ли срок службы электроприбора стандарту а?

3. В лаборатории определяют содержание углерода в 30 пробах нелегиро-

ванной стали. Получены следующие данные: х = 0,19, δ0 (х)= 0,01 По стандар-

ту количество углерода в пробе должно быть равно а = 0,2. При уровне значимости α = 0,05проверить Н0 : х = а при Н1 : х ≠ 0,2 Удовлетворяет ли среднее содержание углерода в пробе стандартному?

163

4. Из двух партий продукции, изготовленных по старой и новой технологиям, взяты выборки объемов n1 = 45 и n2 =40. Расход сырья на единицу продукции по старой технологии x1 = 240 г., а по новой - x2 = 236 г. Генеральные дисперсии равны D(x1)=6,5 D(x2)=8,0. При уровне значимости α = 0,01прове-

рить нулевую гипотезу Н0: х1 = х2 при конкурирующей гипотезе Н1: х1 > х2

Можно ли считать, что расход сырья на изготовление единицы продукции по новой технологии уменьшился?

5. Для исследования колеблемости урожайности свеклы в зависимости от типа внесенных удобрений было засеяно по 10 опытных участков: n1=10, n2=10.

Выборочные дисперсии соответственно равны δ2 (х1 )= 0,55, δ2 (х2 )= 0,47 При уровне значимости α = 0,01 проверить Н0: D(x1)=D(x2) при Н1: D(x1)>D(x2). За-

висит ли колеблемость урожайности свеклы от типа внесенных удобрений?

6. Стандартный срок работы электролампы а=800 часов. В результате выборочной проверки 50 ламп установлено, что средний срок работы х = 790 часов. Среднее квадратическое отклонение генеральной совокупности равно 30 часов. При уровне значимости α = 0,05проверить Но: х = а, если Н1: х ≠ а

Удовлетворяет ли срок работы электролампы стандарту а?

164