
- •МАТЕМАТИКА
- •ЗАДАНИЯ ДЛЯ ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •ВВЕДЕНИЕ
- •Раздел. I. ЛИНЕЙНАЯ АЛГЕБРА
- •Тема 1. Линейная алгебра
- •1.1. Вычисление определителей
- •1.1.1. Вопросы для самостоятельного изучения
- •1.1.1.1. Определения
- •1.1.1.2. Свойства определителей
- •1.1.2. Контрольные вопросы
- •1.2. Действия над матрицами
- •1.2.1. Вопросы для самостоятельного изучения
- •1.2.1.1. Действия над матрицами
- •1.2.1.2. Обратная матрица
- •1.2.1.3. Ранг матрицы
- •1.2.2. Контрольные вопросы
- •1.3. Решение систем линейных алгебраических уравнений
- •1.3.1. Вопросы для самостоятельного изучения
- •1.3.1.1. Метод Крамера решения систем линейных уравнений
- •1.3.1.2. Матричный метод решения систем линейных уравнений
- •1.3.1.3. Метод Гаусса
- •1.3.1.5. Теорема Кронекера–Капели
- •1.3.2. Контрольные вопросы
- •1.3.3. Практическое задание для самостоятельной работы
- •Тема 2. Векторная алгебра
- •2.1. Векторы. Линейные операции над векторами
- •2.1.1. Вопросы для самостоятельного изучения
- •2.1.1.1. Определения
- •2.1.1.2. Линейные операции над векторами
- •2.1.1.3. Координаты вектора, линейные операции над векторами в координатах
- •2.1.1.4. Линейные операции над векторами в координатах
- •2.1.1.5. Деление отрезка в данном отношении
- •2.1.2. Контрольные вопросы
- •2.2. Произведения векторов
- •2.2.1. Вопросы для самостоятельного изучения
- •2.2.1.1. Скалярное произведение векторов
- •2.2.1.2. Векторное произведение векторов
- •2.2.1.3. Смешанное произведение векторов
- •2.2.2. Контрольные вопросы
- •2.3. Комплексные числа
- •2.3.1. Вопросы для самостоятельного изучения
- •2.3.1.1. Определения
- •2.3.1.2. Правила арифметических действий над комплексными числами в алгебраической форме
- •2.3.1.3. Тригонометрическая форма комплексного числа
- •2.3.1.4. Показательная форма комплексного числа. Формула Эйлера
- •2.3.1.5. Действия над комплексными числами в показательной форме
- •2.3.2. Контрольные вопросы
- •2.3.3. Практическое задание для самостоятельной работы
- •Тема 3. Аналитическая геометрия
- •3.1. Основные задачи аналитической геометрии
- •3.1.1. Вопросы для самостоятельного изучения
- •3.1.2. Контрольные вопросы
- •3.2. Кривые второго порядка
- •3.2.1. Вопросы для самостоятельного изучения
- •3.2.2. Контрольные вопросы
- •3.2.3. Практическое задание для самостоятельной работы
- •Раздел. II. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •Тема 4. Предел функции
- •4.1. Элементы теории множеств. Понятие функции
- •4.1.1. Вопросы для самостоятельного изучения
- •4.1.1.1. Элементы теории множеств
- •4.1.1.2. Операции над множествами
- •4.1.1.3. Отображение множеств. Мощность множества.
- •4.1.1.4. Употребление математической символики. Кванторы общности, существования и единственности
- •4.1.1.5. Числовые множества
- •4.1.1.6. Подмножества множества (интервалы)
- •4.1.1.7. Окрестность точки
- •4.1.1.8. Понятие функции
- •4.1.1.9. Элементарные функции, свойства функции
- •4.1.1.10. Четность, нечетность.
- •4.1.2. Контрольные вопросы
- •4.2. Теория пределов
- •4.2.1. Вопросы для самостоятельного изучения
- •4.2.1.1. Числовая последовательность
- •4.2.1.2. Предел числовой последовательности
- •4.2.1.3. Бесконечно малые и бесконечно большие функции
- •4.2.1.4. Предел функции
- •4.2.1.5. Сравнение бесконечно малых функций
- •4.2.1.6. Замечательные пределы
- •4.2.2. Контрольные вопросы
- •4.3. Предел и непрерывность функции
- •4.3.1. Вопросы для самостоятельного изучения
- •4.3.1.1. Односторонние пределы
- •4.3.1.2. Необходимое и достаточное условие существования предела
- •4.3.1.3. Непрерывность функции
- •4.3.1.4. Точки разрыва и их классификация
- •4.3.1.5. Свойства непрерывных функций
- •4.3.2. Контрольные вопросы
- •4.3.3. Практическое задание для самостоятельной работы
- •Тема 5. Дифференциальное исчисление
- •5.1. Вычисление производных
- •5.1.1. Вопросы для самостоятельного изучения
- •5.1.1.1. Производная функции
- •5.1.1.2. Правило дифференцирования по шагам
- •5.1.1.3. Геометрический смысл производной.
- •5.1.1.4. Правила и формулы дифференцирования
- •5.1.1.5. Таблица производных:
- •5.1.1.6. Производная сложной функции
- •5.1.1.7. 1. Логарифмическое дифференцирование
- •5.1.1.8. Производные высших порядков
- •5.1.1.9. . Дифференциал функции, его свойства
- •5.1.2. Контрольные вопросы
- •5.1.3. Практическое задание для самостоятельной работы
- •5.2. Исследование функций на экстремумы и интервалы монотонности
- •5.2.1. Вопросы для самостоятельного изучения
- •5.2.1.1. Условия возрастания и убывания функции
- •5.2.1.2. Точки экстремума функции, необходимое условие экстремума
- •5.2.1.3. Первый достаточный признак экстремума функции
- •5.2.1.4. Схема исследования функции на возрастание, убывание и экстремумы
- •5.2.1.5. Второй достаточный признак экстремума функции
- •5.2.1.6. Второй способ исследования функции на экстремум
- •5.2.1.7. Наибольшее и наименьшее значения функции на отрезке
- •5.2.1.8. Выпуклость, вогнутость графика функции
- •5.2.1.9. Точки перегиба. Необходимое и достаточное условие перегиба.
- •5.2.1.10. Исследование функции на выпуклость, вогнутость, точки перегиба
- •5.2.1.11. Асимптоты графика функции
- •5.2.1.12. Общая схема исследования функции
- •5.2.2. Контрольные вопросы
- •5.3. Исследование функций двух переменных
- •5.3.1. Вопросы для самостоятельного изучения
- •5.3.1.1. Экстремумы функции двух переменных, необходимое условие экстремума
- •5.3.1.2. Достаточные условия экстремума
- •5.3.2. Контрольные вопросы
- •5.3.3. Практическое задание для самостоятельной работы
- •Тема 6. Интегральное исчисление
- •6.1. Решение задач на нахождение неопределенных интегралов. Нахождение неопределенных интегралов различными методами
- •6.1.1. Вопросы для самостоятельного изучения
- •6.1.1.1. Неопределенный интеграл
- •6.1.1.2. Свойства неопределенного интеграла
- •6.1.1.3. Таблица интегралов
- •6.1.1.4. Метод интегрирования по частям
- •6.1.1.5. Рациональные дроби
- •6.1.1.6. Интегрирование простейших рациональных дробей
- •6.1.1.7. Интегрирование рациональных дробей
- •6.1.1.8. Метод замены переменной (метод подстановки)
- •6.1.1.9. Интегрирование иррациональных выражений
- •6.1.2. Контрольные вопросы
- •6.2. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов
- •6.2.1. Вопросы для самостоятельного изучения
- •6.2.1.1. Определение определенного интеграла
- •6.2.1.2. Свойства определенного интеграла:
- •6.2.1.3. Вычисление определенного интеграла, физические приложения определенного интеграла
- •6.2.1.4. Интегрирование по частям в определенном интеграле
- •6.2.1.5. Формула замены переменной в определенном интеграле
- •6.2.1.6. Приложения определенного интеграла
- •6.2.1.7. Площадь плоской фигуры
- •6.2.1.8. Объем тела вращения
- •6.2.1.9. Несобственные интегралы с бесконечным верхним пределом интегрирования
- •6.2.2. Контрольные вопросы
- •6.2.3. Практическое задание для самостоятельной работы
- •7.1. Сходимость знакоположительных рядов
- •7.1.1. Вопросы для самостоятельного изучения
- •7.1.1.1. Числовой ряд, сумма ряда, свойства рядов
- •7.1.1.2. Необходимый признак сходимости ряда
- •7.1.1.3. Признаки сходимости знакоположительных рядов
- •7.1.2. Контрольные вопросы
- •7.2. Исследование сходимости знакочередующихся рядов
- •7.2.1. Вопросы для самостоятельного изучения
- •7.2.1.1. Знакочередующиеся ряды, признак Лейбница
- •7.2.1.2. Признак абсолютной сходимости знакопеременного ряда
- •7.2.1.3. Схема исследования знакочередующихся рядов на сходимость
- •7.2.2. Контрольные вопросы
- •Тема 8. Функциональные ряды
- •8.1. Нахождение интервала и радиуса сходимости степенных рядов
- •8.1.1. Вопросы для самостоятельного изучения
- •8.1.1.1. Функциональные ряды
- •8.1.1.2. Область сходимости степенного ряда
- •8.1.1.3. Схема нахождения области сходимости степенного ряда
- •8.1.1.4. Ряд Тейлора
- •8.1.1.5. Разложение основных элементарных функций в степенные ряды
- •8.1.2. Контрольные вопросы
- •8.1.3. Практическое задание для самостоятельной работы
- •Раздел. IV. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- •Тема 9. Численные методы
- •9.1. Нахождение корней уравнений итерационным методом
- •9.1.1. Вопросы для самостоятельного изучения
- •9.1.1.1. Постановка задачи
- •9.1.1.2. Графический метод
- •9.1.1.3. Отделение корней
- •9.1.1.4. Метод деления отрезка пополам
- •9.1.1.5. Метод хорд
- •9.1.1.6. Метод итераций
- •9.1.1.7. Достаточное условие применимости метода итераций
- •9.1.2. Контрольные вопросы
- •9.2. Примеры численного интегрирования
- •9.2.1. Вопросы для самостоятельного изучения
- •9.2.1.1. Формулы прямоугольников
- •9.2.1.2. Формула трапеций
- •9.2.1.3. Формула Симпсона
- •9.2.2. Контрольные вопросы
- •9.3. Примеры численного интерполирования
- •9.3.1. Вопросы для самостоятельного изучения
- •9.3.1.1. Интерполяционная формула Лагранжа
- •9.3.1.2. Интерполяционная формула Ньютона
- •9.3.1.3. Линейное интерполирование
- •9.3.2. Контрольные вопросы
- •Раздел. V. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- •Тема 10. Случайные события
- •10.1. Задачи на вычисление классической вероятности и относительной частоты
- •10.1.1. Вопросы для самостоятельного изучения
- •10.1.1.1. Случайные события
- •10.1.1.2. Определение вероятности события
- •10.1.1.3. Теоремы сложения и умножения. Условная вероятность
- •10.1.1.4. Формула полной вероятности и формула Байеса
- •10.1.2. Контрольные вопросы
- •Тема 11. Случайные величины
- •11.1. Законы распределения случайной величины
- •11.1.1. Вопросы для самостоятельного изучения
- •11.1.1.1. Случайные величины
- •11.1.1.2. Дискретная случайная величина
- •11.1.1.3. Непрерывная случайная величина
- •11.1.1.4. Нормальный закон распределения случайной величины
- •11.1.1.5. Биномиальный закон распределения. Формула Бернулли
- •11.1.2. Контрольные вопросы
- •Тема 12. Математическая статистика
- •12.1. Методы математической статистики
- •12.1.1. Вопросы для самостоятельного изучения
- •12.1.1.1. Случайная выборка из генеральной совокупности, ее табличное представление
- •12.1.1.2. Графическое представление случайной выборки
- •12.1.1.3. Точечные и интервальные оценки
- •12.1.1.4. Проверка статистических гипотез
- •12.1.2. Контрольные вопросы
- •12.1.3. Практическое задание для самостоятельной работы
- •РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Тема 3. Аналитическая геометрия
3.1. Основные задачи аналитической геометрии
3.1.1. Вопросы для самостоятельного изучения
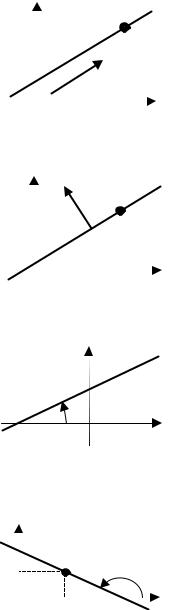
ТАБЛИЦА 3.1.1. УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
Ax + By + C = 0 (ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ), A2 + B2 ≠ 0
Название |
|
|
Уравнение |
|
|
|
Смысл |
|
|
|
Геометрическое |
||||||||||||||||
уравнения |
|
|
|
|
параметров |
|
|
|
|
изображение |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1. Каноническое |
|
x − x0 |
= |
y − y0 |
|
M0 (x0 , y0 ) |
– точ- |
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
уравнение |
пря- |
|
m |
n |
|
|
|
|
|
y0 |
|
|
|
M0 |
|||||||||||||
|
|
|
ка на прямой, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
мой. |
|
|
|
|
|
|
|
S = (m,n) |
– на- |
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
правляющий век- |
|
|
|
|
O |
|
|
x0 |
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
тор прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Уравнение пря- |
|
A(x − x ) + |
|
M |
0 |
(x , y ) – точ- |
|
|
y |
|
|
N |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
мой |
с нормаль- |
|
+B( y − y0 ) = 0 |
|
ка на прямой, |
|
|
|
y0 |
|
|
|
|
|
M0 |
||||||||||||
ным вектором. |
|
|
|
|
|
N = (A, B) |
– |
нор- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мальный |
вектор |
|
|
O |
|
|
|
|
x0 |
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. Уравнение |
пря- |
|
y = kx + b |
|
k = tg α – угловой |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||||
мой с угловым ко- |
|
|
|
|
|
коэффициент, |
|
|
|
|
|
|
|
α |
} |
b |
|
|
|
|
|||||||
эффициентом. |
|
|
|
|
|
|
b – отрезок, отсе- |
|
|
|
|
|
|
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
каемый |
на |
оси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Oy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4. Уравнение |
пря- |
|
y − y0 = |
|
k = tg α – угловой |
|
y |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
мой, |
проходящей |
|
= k(x − x0 ) |
|
коэффициент, |
|
y0 |
|
|
|
|
M0 |
α |
||||||||||||||
через данную точ- |
|
|
|
|
|
M0 (x0 , y0 ) |
– |
точ- |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
O |
|
|
|
|
x0 |
|
|
|
|
x |
||||||||||||||
ку в |
данном |
на- |
|
|
|
|
|
ка на прямой. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
правлении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
|
Название |
Уравнение |
Смысл |
|
Геометрическое |
||||||
|
уравнения |
параметров |
изображение |
|
|||||||
|
|
|
|
|
|
||||||
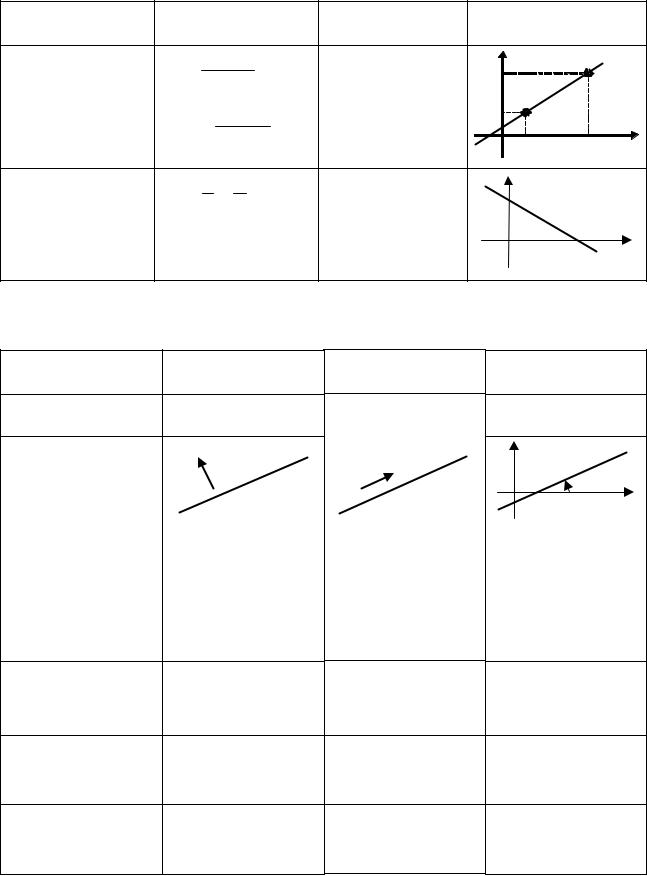
5. |
Уравнение пря- |
x − x0 |
= |
M0 (x0 , y0 ) , |
|
y |
|
|
|
||
мой, проходящей |
x |
− x |
M1(x1, y1) – точки |
y1 |
|
M1 |
|
||||
1 |
|
0 |
M0 |
|
|
||||||
через две точки |
= |
y − y0 |
на прямой. |
|
y0 |
|
|
|
|||
y1 |
− y0 |
|
O |
x0 |
x1 |
x |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
6. |
Уравнение пря- |
x |
+ |
y |
=1 |
a, b – отрезки, от- |
y |
|
|
|
|
мой в отрезках. |
a |
b |
секаемые на осях |
|
|
|
|
||||
|
|
b |
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
координат. |
|
O |
a |
|
x |
|
ТАБЛИЦА 3.1.2. ХАРАКТЕРИСТИКИ НАПРАВЛЕНИЯ ПРЯМОЙ l |
|
|
||||||||
|
|
|
|
И ПРЯМЫХ l1 || l , l2 l |
|
|
|
|
|
||
|
Определение, |
Нормальный |
Направляющий |
|
Угловой |
|
|||||
|
формула |
|
вектор |
вектор |
|
|
коэффициент |
||||
1. |
Обозначение. |
N = (A, B) |
S = (m,n) |
|
k |
|
|
||||
2. |
Изображение, |
|
N |
|
|
S |
|
y |
|
|
l |
определение. |
|
|
l |
l |
O |
|
ϕ |
||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
N |
– вектор, пер- S – вектор, |
парал- k = tg ϕ, |
|
|
||||||
|
пендикулярный |
лельный прямой l. |
ϕ |
– угол |
наклона |
||||||
|
прямой l. |
|
|
|
прямой l к оси Ox. |
||||||
3. |
Формулы связи. |
k = −A / B, |
k = n / m, |
|
S = (1,k), |
|
|||||
|
|
S = (B,−A) |
N = (n,−m) |
|
N = (k,−1) |
|
|||||
4. |
Направление |
|
N1 = N |
S1 = S |
|
|
k1 = k |
|
|||
прямой l1 (l1 || l ). |
|
|
|
|
|
|
|
|
|
|
|
5. |
Направление |
|
N2 = S |
S2 = N |
|
|
k2 = − 1 |
|
|||
прямой l2 (l2 l ). |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
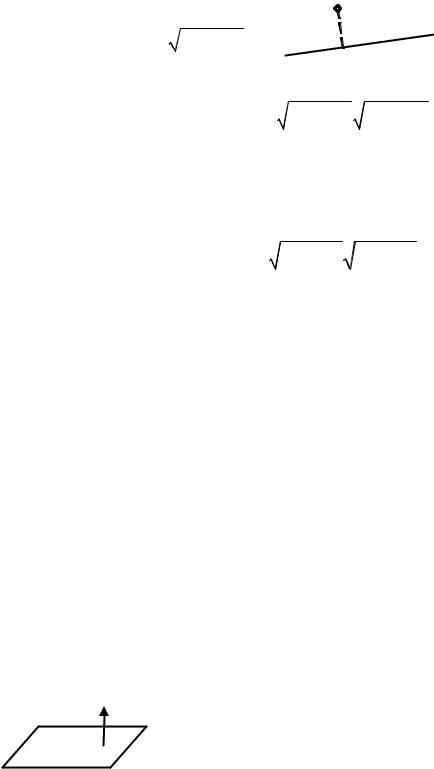
ТАБЛИЦА 3.1.3. ОСНОВНЫЕ ЗАДАЧИ НА ПРЯМУЮ В ПЛОСКОСТИ
|
|
|
|
|
|
Задача |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
||||||||||||||||||
1. Проверить принадлежность |
точки |
Точка M лежит на прямой, если |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
M (x1, y1) прямой Ax + By + C = 0. |
|
Ax1 + By1 + C = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2. Найти |
|
|
расстояние |
d |
от |
точки |
d = |
|
Ax1 + By1 + C |
|
|
|
|
|
|
|
|
|
|
|
M (x1, y1) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
M (x1, y1) |
до прямой Ax + By + C = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
A2 + B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. Найти угол ϕ между прямыми |
|
а) |
cosϕ = |
|
|
|
N1 N2 |
= |
|
|
|
|
A1 A2 + B1B2 |
|
|
; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
а) A1x + B1 y + C1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
|
N2 |
|
|
|
|
|
|
|
|
|
A2 + B2 |
A2 + B2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
2 |
2 |
|
|||
|
A2 x + B2 y + C2 |
= 0 ; |
|
|
|
|
|
|
б) tg ϕ = |
k2 − k1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
б) y = k x + b , y = k |
|
x + b ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
1 + k2k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
x − x1 |
= |
|
y − y1 |
, |
x − x2 |
= |
y − y2 |
. |
|
|
|
|
|
|
|
|
|
|
S S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m m + n n |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
в) |
cosϕ = |
|
|
|
1 |
|
|
|
|
|
2 |
|
= |
|
|
|
|
|
1 |
|
2 |
|
1 |
2 |
|
. |
|
|||||||||||||||||||
m1 |
|
n1 |
|
|
m2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
S2 |
|
|
|
|
|
|
|
|
|
|
m2 |
+ n2 |
m2 |
+ n2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
2 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
4. Проверить параллельность прямых. |
а) |
N |
|| N |
|
|
|
A1 |
= B1 ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) k = k |
2 |
; в) S || S |
2 |
|
m1 |
= |
n1 |
. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Проверить |
перпендикулярность |
а) |
N N |
2 |
A A + B B = 0; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
||||||||||
прямых. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
k1 k2 = −1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) S1 S2 m1m2 + n1n2 = 0 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
6. Найти точку пересечения прямых |
Решить систему уравнений |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
A1x + B1 y + C1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
A1x + B1 y + C1 = 0, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
A x + B y + C |
2 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
A x |
+ B y |
+ C |
2 |
= 0 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ТАБЛИЦА 3.1.4. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
Понятие |
|
|
|
|
|
|
Изображение |
|
|
|
|
|
|
|
|
|
|
|
Уравнение, формула |
|
|
|
|||||||||||||||||||||||||||||||||||
1. Общее |
|
|
уравнение |
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
Ax + By + Cz + D = 0 , |
|
|
|
|||||||||||||||||||||||||||||||||
плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
где N = (A, B,C) |
– нормальный век- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тор плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
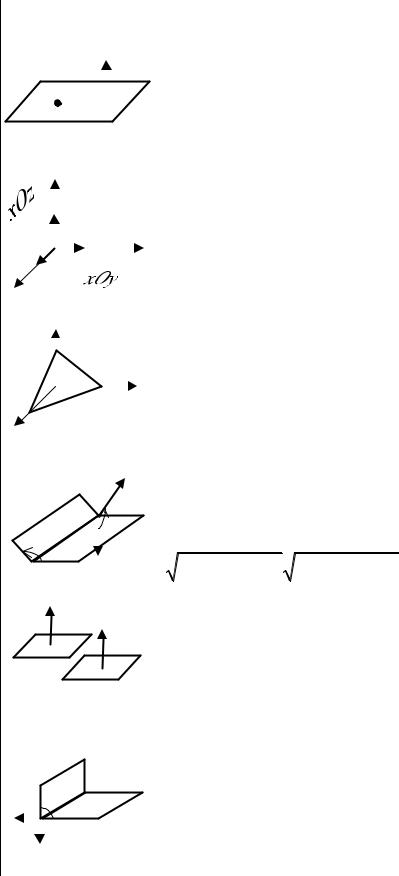
|
Понятие |
|
|
Изображение |
|
|
Уравнение, формула |
|||||||||||||||||||||||||||
2. Уравнение плоскости |
|
|
|
|
|
|
|
|
|
|
|
A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 , |
||||||||||||||||||||||
с |
нормальным |
векто- |
|
|
|
|
|
|
|
|
N |
где N = (A, B,C) |
– нормальный век- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ром. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
M0 |
|
|
|
|
|
тор, M0 (x0 , y0 , z0 ) – точка на плос- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Частные случаи: |
|
|
z |
|
|
|
|
yOz |
а) N = k = (0,0,1) z = 0; |
|
|
|||||||||||||||||||||||
а) плоскость xOy ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
k |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) плоскость xOz ; |
|
|
|
|
|
|
|
|
|
б) N = j = (0,1,0) y = 0; |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x |
|
i |
|
|
|
y |
в) N = i = (1,0,0) x = 0. |
|
|
|||||||||||||||||||||||
в) плоскость yOz . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. Уравнение плоскости |
|
|
z c |
|
|
|
|
|
|
|
|
x |
+ |
y |
+ |
|
z |
|
=1, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
в отрезках. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
c |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где a, b, c – величины отрезков, от- |
|||||||||||||||||||
|
|
|
|
a |
|
|
|
|
b y |
|
секаемых на осях координат (с уче- |
|||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
том знака). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Угол между плоско- |
|
|
|
|
|
|
|
|
N2 |
|
|
cosφ = |
|
|
|
N1 N2 |
|
|
= |
|
|
|||||||||||||
стями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
N1 | | N2 | |
|
|
|||||||||||||||||||
|
|
|
ϕ |
|
|
|
|
|
ϕ |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
A x + B y + C z + D = 0, |
|
|
|
|
N |
|
|
|
|
|
= |
|
A1 A2 + B1B2 + C1C2 |
|
. |
|||||||||||||||||||
1 |
1 |
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
A2 |
+ B2 + C2 |
A2 + B2 |
|
|||||||||||||||||||||||
A2 x + B2 y + C2 z + D2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
+ C2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
2 |
|
2 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. Условие |
параллель- |
|
|
|
|
N1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ности плоскостей |
|
|
|
|
|
|
|
N2 |
|
|
|
|
|
N1 || |
N2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
A x + B y + C z + D = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
= |
B1 |
= |
C1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
B2 |
|
C2 |
|
|
||||||||
A2 x + B2 y + C2 z + D2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7. Условие |
перпендику- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лярности плоскостей |
N 2 |
|
|
|
|
|
|
|
|
|
|
|
|
N1 N2 |
|
|
||||||||||||||||||
A1x + B1 y + C1z + D1 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
A1 A2 + B1B2 + C1C2 = 0 |
|||||||||||||||||||||
|
|
|
N1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
A2 x + B2 y + C2 z + D2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33
|
|
|
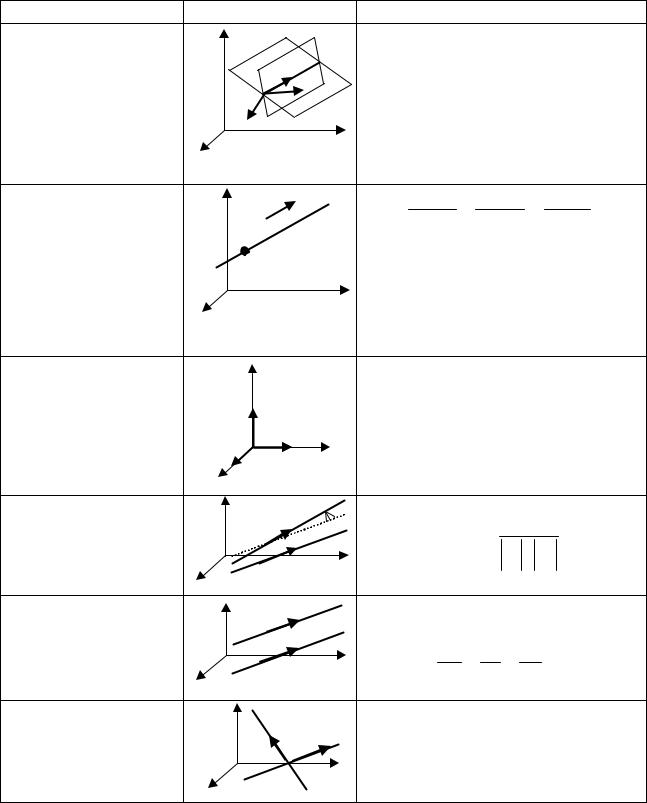
ТАБЛИЦА 3.1.5. ПРЯМАЯ В ПРОСТРАНСТВЕ |
|
|
||||||||||||||
Понятия |
|
Изображения |
|
|
|
|
|
Уравнение (формула) |
|||||||||||
1. Общие |
|
уравнения |
z |
|
|
|
|
A x + B y + C z + D = 0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
прямой. |
|
|
|
|
S |
N1 |
A2 x + B2 y + C2 z + D2 = 0 |
||||||||||||
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
нормальные |
||||
|
|
|
|
|
N = (A , B ,C ) |
||||||||||||||
|
|
|
|
O |
|
|
|
векторы |
|||||||||||
|
|
|
x |
|
y |
N |
|
1 |
|
|
1 |
1 |
1 |
) |
|
||||
|
|
|
|
|
2 |
= (A , B ,C |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
плоскостей. |
|||||
2. Канонические |
z |
S |
|
|
|
|
|
|
x − x0 |
= y − y0 |
= z − z0 , |
||||||||
уравнения прямой. |
|
|
|
|
|
|
|
|
m |
|
|
|
n |
p |
|||||
|
|
|
|
M0 (x0 , y0 , z0 ) |
где |
S = (m,n, p) |
|
– |
направляющий |
||||||||||
|
|
|
x |
O |
|
y вектор, M0 (x0 , y0 , z0 ) – точка на |
|||||||||||||
|
|
|
|
|
|
|
прямой. |
|
|
|
|
|
|
|
|||||
3. Частные случаи: |
z |
|
|
а) |
|
S = i = (1,0,0) z = 0, y = 0 |
|||||||||||||
а) ось Ox; |
|
|
|
|
|
|
|||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) ось Oy; |
|
|
j |
|
б) S = j = (0,1,0) x = 0, z = 0 |
||||||||||||||
|
|
|
|
||||||||||||||||
в) ось Oz. |
|
|
O |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
i |
в) |
|
S = k = (0,0,1) x = 0, y = 0 |
|||||||||||||
4. Угол |
между |
пря- |
z |
S2 |
ϕ |
|
|
|
|
|
|
|
|
|
|
|
S1 S2 |
||
мыми. |
|
|
|
O |
|
|
|
|
|
|
|
cosϕ = |
|||||||
|
|
|
|
|
|
|
|
|
|
|
S1 |
S2 |
|||||||
|
|
|
x |
S1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Условие |
|
парал- |
z |
S2 |
|
S1 = (m1,n1, p1) , S2 = (m2 ,n2 , p2 ) |
|||||||||||||
лельности прямых. |
O |
|
|
S |
|
|| S |
|
m1 |
= n1 = p1 |
||||||||||
|
|
|
x |
S1 |
y |
|
2 |
||||||||||||
|
|
|
|
|
1 |
|
|
|
m2 |
|
|
n2 |
|
p2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. Условие |
перпенди- |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
кулярности прямых |
O |
S2 |
S1 |
S1 |
S2 m1m2 + n1n2 + p1 p2 = 0 |
||||||||||||||
|
|
|
|
y |
|||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
