Раздел 2 Методы построения и формы представление аналитических математических моделей

Тема 2.1 Методика создания концептуальных аналитических моделей

§ 2. 1. 1 Методика создания математических моделей на микро уровне

Учебные элементы:

1. Микро, макро и мета уровни для концептуальных ММ.

2. Система координат для фазовых переменных.

3. Законы сохранения: массы, энергии, количества движения.

4. Модель с сосредоточенными параметрами.

В зависимости от места в иерархии описаний мм делятся, как относящиеся к микро, макро, и мета - уровням.

Особенностью ММ на микро уровне является отражение физических процессов, протекающих в непрерывном пространстве и времени. Типичные ММ на микро уровне — дифференциальные уравнения в частных производных (ДУЧП). В них независимыми переменными являются пространственные координаты (x, y, z) и время t.

ДУЧП представляют собой математическое выражение законов сохранения субстанции (вещества, энергии, количества движения):

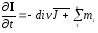( 2.1)

В этом выражении: І — количество субстанции, аккумулируемое в единице объёма (единиц).

Если V = dx∙dy∙dz, то V І 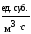— объёмная концентрация;

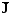—вектор переноса субстанции через поверхность, окружающую выделенный объём, ;

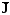
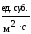m_i — мощность источника субстанции, если он находится внутри выделенного объёма — .

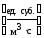Уравнения сохранения могут быть записаны в двух фундаментально различных системах координат. Одна из них называется системой координат Лагранжа. В этой системе начало координат тесно связано с конкретной материальной частью субстанции (тело, система). При этой материальной системе перемещается и система координат, а наблюдение сосредоточено за движением материальной системы (рис. 2.1а).

Другая система координат называется системой координат Эйлера (рис 2.1б). Эта система координат фиксирована в пространстве. В данном случае, чтобы описать движение материальной субстанции фиксируется объём пространства, в который попадает и который затем покидает субстанция, т.е. в координатах Лагранжа фиксируют материальную систему, а в координатах Эйлера — объём.

В статике, когда субстанция не движется, эти системы координат совпадают.

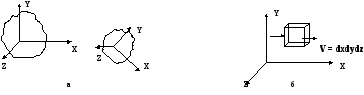
Рис. 2.1 Система координат Лагранжа (а) и Эйлера (б)

Общее выражение для закона сохранения (1.5) записано для системы координат Эйлера.

Учитывая, что дивергенция вектора:

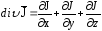, (2.2)

а вектор переноса субстанции 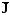, называемый также потоком субстанции, в общем случае содержит две составляющие: конвективную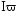и кондуктивную (диффузионную) (Δ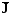), т.е. 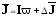, можно получить для каждой субстанции дифференциальное уравнение в частных производных ( — скорость, м / с).

Например, для закона сохранения массы вещества:

Ι = ρ [кг / м ^-3] ,а кондуктивная составляющая определяется законом Фика.

Δ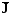= -D∙ grad C (2.3)

где: D — коэффициент диффузии, [м² / с];

С — концентрация, [кг / м ^–3 ] (С  ρ).

Если внутри объёма нет источников, генерирующих массу, то уравнение (2.1) записывается в следующем виде:

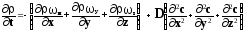(2.4)

Это дифференциальное уравнение в частных производных второго порядка.

Для закона сохранения энергии:

Ι = ρ∙е,

где: е — удельная энергия единицы массы вещества [Дж / кг]

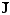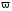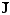= ρ∙е∙+Δ, [Вт / м²] (2. 5)

По закону Фурье:

Δ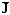= —∙grad T (2. 6)

тогда уравнение сохранения энергии запишется в виде:

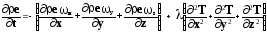(2.7)

При  = const , ρ = const , e = c∙T ,

где: с — удельная теплоёмкость [Дж / кг ∙ град] получается уравнение переноса тепла Фурье — Кирхгофа:

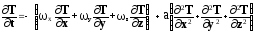(2.8)

В случае если тепло переносится в неподвижной среде  = 0 и рассматривается перенос тепла только по координате х, получаем уравнение теплопроводности (Фурье) через плоскую стенку:

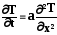(2.9)

где: 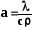— коэффициент температуропроводности,- м²/с

Для закона сохранения количества движения (баланс сил в потоке):

Ι = ρ∙ω [кг∙м^-3 ∙ м∙с^-1] , по аналогии

Δ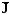= — ν ∙grad ω (2.10)

Поскольку  вектор, необходимо записать уравнение для каждой координаты. Например, для координаты x при постоянной плотности ρ, где g – ускорение силы тяжести, а dp/ dx – градиент давления по координате x, ν – коэффициент кинематической вязкости - м²/с

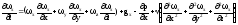
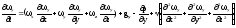(2.11)

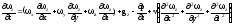
Два других уравнения по координатам y, z получаются, если заменить соответствующие индексы в уравнении для координаты x .

Уравнения 2.4, 2.8, 2.11 нужно дополнить уравнением состояния

Pυ = RT (2.12)

и краевыми условиями.

Краевые условия включают в себя пространственное распределение параметров (скорости, температуры, давления) в начальный момент времени (начальные условия) и законы взаимодействия между объектом и окружающей средой (граничные условия). Граничные условия представляют собой функции распределения параметров на границе и задаются несколькими способами.

Например, для параметра Т различают граничные условия первого рода:

T_s= T(x, y, z, t);

Граничные условия второго рода задаются функцией для теплового потока Q, а граничные условия третьего рода связывают температуру на границе с температурой окружающей среды через заданное значение коэффициента теплоотдачи α.

Общее аналитическое математическое описание фиксированного объёма можно записать в таком виде как систему уравнений:

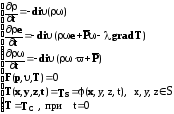(2.13)

Это математическая модель объекта (определенного объема) на микро уровне. В уравнениях (2.12) есть переменная, _P которая называется тензор давления в фиксированном объёме. Поясним значение этого понятия. Из математики известно понятие скаляр — величина, полностью характеризуемая своим численным значением в выбранной системе единиц (температура, плотность и т.п.).

Есть и другое определение: скаляр — это тензор нулевого ранга 3⁰ = 1.

Вектор — величина, характеризуемая в пространстве тремя величинами (три проекции на оси координат или модуль и два угла по отношению к осям координат).

Вектор — это тензор первого ранга 3¹ = 3.

Тензор (лат. tendo — напрягаю, растягиваю) обобщенное понятие вектора.

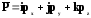
где: 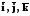— орты;

P_X , P_Y , P_Z — векторы, составляющие тензор 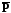по 3-м координатам.

Так как каждый вектор характеризуется тремя величинами, то тензор описывается уже 9-тью величинами, т.е. это тензор 2-го ранга 3² = 9.

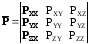—матрица 3х3

Обращает внимание аналогия коэффициента теплопроводности с коэффициентом диффузии и кинематической вязкости.