Численное решение задачи Коши

y(n)) = f(x, y, y', y'', ..., y(n-1)),

y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1

состоит в построении таблицы приближенных значений yi решения y=y(x) в точках x1, x2, ..., xi, ... .

Задача о численном решении дифференциального уравнения порядка выше первого чаще всего сводится к численному решению решению задачи Коши для нормальной системы дифференциальных уравнений.

Обозначив

y(x)=y1(x), y'(x)=y2(x), y''(x)=y3(x), ..., y(n-1)(x)=yn (x),

получим задачу Коши для системы n дифференциальных уравнений 1-го порядка

y1'=y2 , y2'=y3 , ..., yn' =f(x, y1, y2 , ..., yn ),

y1(x0 )=y0, y2(x0)=y1,0 , ..., yn-1(x0)=yn-1,0,

которая в векторной форме имеет вид

`Y '= `F(x,`Y), `Y(x0) =`Y0,

`Y (x)=(y1(x), y2(x), ..., yn(x)), `Y '(x)=(y1'(x), y2'(x), ..., yn'(x)),

`F(x,`Y)= (y2, y3, ..., yn, f(x, y1, y2 , ..., yn )).

Вирішення диференціальних рівнянь методом Рунге-Кутта. Опис методу.

Метод Рунге-Кутта найбільш частіше виконується при чисельному вирішенні задачі Коші і дає можливість отримати наближення рішення високої точності.

Нехай на відрізку [a, b] потрібно знайти чисельне значення рішення диференційного рівняння

(1)

з початковою умовою

Розіб’ємо відрізок [a,b] на n рівних частин точками , деh=(b-a)/n i знайдемо наближені значення рішення диференційного рівняння в точкахПрийдемо до відрізку () і необхідності знаходження(мал. 3).

В методі Рунге – Кутта, як і в методі Ейлера, послідовні наближені значення у_і шуканої функції визначаються за формулою

Якщо розкласти функцію у в (1) у ряд Тейлора та обмежитися членами до h⁴ (четвертого порядку малості) включно, то приріст функції у можна предcтавити у вигляді

, (2)

де похідні визначаються послідовним диференціюванням з рівняння (1).

Замість беспосередніх обчислень за формулою (2) в методі Рунге-Кутта четвертого порядка знаходяться чотири числа наступним чином.

Знаходимо k^(і-1)₁=h f() – напрямок дотичноїдо інтегральної кривої у точці з точністю до множника h і точку перетину прямих і , тобто точку(див мал. 3).

Знаходимо напрямок дотичної в точці :

і із точки проводимо пряму зкутовим коефіцієнтом до перетину з прямою

Отримуємо точку .

Знаходимо напрямок дотичної в точці

і із точки проведемо пряму з кутовим коефіцієнтом до перетину з прямою .

Отримуємо точку Потім знаходимо напрямок дотичної в точці:

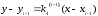Проведемо із точки прямуз кутовим коефіцієнтом k₄^(і-1) до перетину з прямою . В точці, де, і буде знаходитися наближене значення рішення для.

Мал. 3. Геометрична інтерпретація методу Рунге-Кутта.

Таким чином ми отримали 4 числа :

k^(i-1)₁= h f() (3)

(4)

(5)

(6)

Можна доказати, що якщо числам k₁, k₂, k₃, k₄ надати відповідні вагові коефіцієнти ,,,, то середньозважене цих чисел, тобто

,

з точністю до четвертих степеней дорівнює значенню у_і-1, обчисленому по формулі (7):

(7)

Основна формула для обчислення за методом Рунге-Кутта четвертого порядка:

, (8)

в якій для кожної і-ї пари поточних значень х_і та у_і за формулами (3)-(6) визначаються кутові коефіцієнти і за формулою (7) знаходиться у_і-1.

Метод Рунге –Кутта має порядок точності h⁴ на всьому відрізку [a, b]. Оцінка точності метода досить важка. Грубу оцінку похибки ми можемо отримати за допомогою „подвійного прорахунка” за формулою:

|y_i^*-y(x_i)| ,

де y(x_i) – значення точного рішення рівняння (1) в точці х_і, а y_i^* та y_i - наближені значення, отримані з кроком h/2 та h.

Якщо  - задана точність рішення, то число n (число подрібнення для визначення кроку інтегрування h=(b-a)/n) береться таким чином, щоб h⁴<. Але крок розрахунку можна змінювати при переході від однієї точки до іншої.

Для оцінки вірності вибору кроку h використовують рівність

,

де q повинно дорівнювати декільком сотим, в іншому випадку крок h необхідно зменшувати.

Метод Рунге –Кутта можна також застосовувати і для вирішення систем диференційних рівнянь.

Нехай задається система диференційних рівнянь першого порядка

з початковими умовами

х=х₀, у(х₀)=у₀, z(х₀)=z₀.

Для цього випадку на і-му кроці інтегрування паралельно визначаються числа y_i та z_i:

,

,

де k⁽ⁱ⁾₁= h ,

l⁽ⁱ⁾₁= h ;

,

Тоді вирішення системи для (і+1)-го кроку , .