§ 3.2.3. Методика оценки адекватности эмпирических моделей
При анализе численной последовательности, полученной экспериментально, возможны три варианта:
Х – неслучайная и Y – неслучайная величины. Математическая модель у = f(x). Адекватность модели оценивается на основе погрешности измерительных приборов.
Х – неслучайная величина, Y – случайная величина.
Y = φp (X) – регрессионная модель .
Х – случайная величина, Y – случайная величина.
Y = Fk (X) – корреляционная модель .
Адекватность полученного математического описания (уравнения регрессии)– соответствие модели (отклонение данных модели от экспериментальных данных) экспериментальным данным по заданному критерию.
Количественная оценка адекватности может проводиться двумя методами.
Путем определения средней ошибки аппроксимации по формуле
(3.7)
где N – количество опытных данных, используемых для получения коэффициентов в уравнении регрессии;
Yм(i) – значение зависимого параметра, рассчитанного по уравнению регрессии;
Yо(i)- значение зависимого параметра, полученного в эксперименте.
Критерием допустимой погрешности аппроксимации является выражение 10.
Путем статистической оценки результатов на основе критерия Фишера.
Статистическое распределение, которое позволяет проверять гипотезу о равенстве двух дисперсий, называют распределением Фишера F (таблица 3.2).
Проверка гипотезы адекватности осуществляется путем сравнения дисперсии опытных данных относительно уравнения регрессии Sост и дисперсии случайной ошибки измерений. Считается, что уравнение регрессии адекватно описывает исследуемый объект, если остаточная дисперсия Sост исходной величины не превышает погрешности опыта.
Однако, для оценки дисперсии опыта, необходимо иметь несколько значений исходного параметра, полученных при одинаковых условиях.
Если параллельные опыты провести не удается, то проводится оценка качества аппроксимации полученных данных принятому математическому описанию. В этом случае сравнивают дисперсию относительно среднего значения опытных данных Sy и остаточную дисперсию.
Уравнение регрессии имеет смысл, если дисперсия относительного среднего Sy существенно больше, чем остаточная дисперсия Sост. Для этого исчисляется критерий Фишера Fр, а потом находят его табличное значение FT(f1,f2).
f1 - число степеней свободы числителя - f1=N-1;
f2 - число степеней свободы знаменателя - f2=N-n-1;
Степень свободы – число экспериментальных точек, которые можно использовать для оценки дисперсии.
N - количество опытных данных;
n - количество независимых переменных в уравнении регрессии.
Оценка адекватности проводится по следующему алгоритму:
1. Получают массив опытных данных X0(i); Y0(i) в количестве N (табличная функция);
2. Оценивают статистические характеристики опытных данных:
1. среднее значение
(математическое ожидание).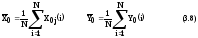
2. среднеквадратичное
отклонение и дисперсию S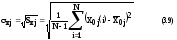
3. Методом наименьших
квадратов получают уравнение регрессии,
например, для линейной модели (с n=1 одна
независимая переменная);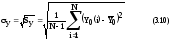
4. Вычисляют по
уравнению регрессии массив значений
YM(i);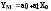
5. Оценивают статистические характеристики регрессионных значений YM, Sост. разброс значений вычисленных за уравнением регрессии относительно опытных данных:
6. Находят значение
критерия Фишера по отношению дисперсий
Sy
и Sост,
как отношение: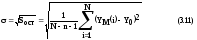
7. Находят по таблице
критерий Фишера как функцию трех
переменных: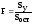
где q
- степень значимости.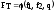
8. Сравнивают Fр и FT и делают вывод. Уравнение регрессии имеет смысл при условии Fp > FT. Чем больше Fp превышает FT, тем эффективнее уравнение регрессии.
Значение критерия
Фишера
Таблица 3.2.
|
Число степеней свободы знаменате-ля |
Число степеней свободы числителя
| ||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
48 | |
|
1 |
161,4 |
199,5 |
215,7 |
224,6 |
230,2 |
234,0 |
243,9 |
249,9 |
254,3 |
|
2 |
18,5 |
19,0 |
19,2 |
19,3 |
19,3 |
19,4 |
19,5 |
19,5 |
19,5 |
|
3 |
10,1 |
9,6 |
9,3 |
9,1 |
9,0 |
8,9 |
8,7 |
8,6 |
8,5 |
|
4 |
7,7 |
6,9 |
6,6 |
6,4 |
6,3 |
6,2 |
5,9 |
5,8 |
5,6 |
|
5 |
6,6 |
5,8 |
5,4 |
5,2 |
5,1 |
5,0 |
4,7 |
4,5 |
4,4 |
|
6 |
6,0 |
5,1 |
4,8 |
4,5 |
4,4 |
4,3 |
4,0 |
4,0 |
3,7 |
|
7 |
5,6 |
4,7 |
4,4 |
4,1 |
4,0 |
3,9 |
3,6 |
3,4 |
3,2 |
|
8 |
5,3 |
4,5 |
4,1 |
3,8 |
3,7 |
3,6 |
3,3 |
3,1 |
2,9 |
|
9 |
5,1 |
4,3 |
3,9 |
3,6 |
3,5 |
3,4 |
3,1 |
2,9 |
2,7 |
|
10 |
5,0 |
4,1 |
3,7 |
3,5 |
3,3 |
3,2 |
2,9 |
2,7 |
2,5 |
|
11 |
4,8 |
4,0 |
3,6 |
3,4 |
3,2 |
3,1 |
2,8 |
2,6 |
2,4 |
|
12 |
4,8 |
3,9 |
3,5 |
3,3 |
3,1 |
3,0 |
2,7 |
2,5 |
2,3 |
|
13 |
4,7 |
3,8 |
3,4 |
3,2 |
3,0 |
2,9 |
2,6 |
2,4 |
2,2 |
|
14 |
4,6 |
3,7 |
3,3 |
3,1 |
3,0 |
2,9 |
2,5 |
2,3 |
2,1 |
|
15 |
4,5 |
3,7 |
3,3 |
3,1 |
2,9 |
2,8 |
2,5 |
2,3 |
2,1 |
|
30 |
4,2 |
3,3 |
2,9 |
2,7 |
2,5 |
2,4 |
2,1 |
1,9 |
1,6 |
|
40 |
4,1 |
3,2 |
2,9 |
2,6 |
2,5 |
2,3 |
2,0 |
1,8 |
1,5 |
|
60 |
4,0 |
3,2 |
2,8 |
2,5 |
2,4 |
2,3 |
1,9 |
1,7 |
1,4 |
|
120 |
3,9 |
3,1 |
2,7 |
2,5 |
2,3 |
2,2 |
1,8 |
1,6 |
1,3 |
|
|
3,8 |
3,0 |
2,6 |
2,4 |
2,2 |
2,1 |
1,8 |
1,5 |
1,0 |
В табл. 3.2 приведены значения критерия Фишера F для уровня значимости q=0.05.
Рассмотрим пример.
Результаты опытов приведены в таблице 3.3
Таблица 3.3
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
yo |
0 |
0 |
1 |
2 |
3 |
Повторных опытов нет. Проверяем оценку качества аппроксимации полученных данных принятому математическому описанию.
Математическое ожидание yo = 1.2
Дисперсия относительно среднего sy=((yo-1.2)2)/4= 1.7
Остаточная дисперсия sост=((yo- yм)2)/3= 0.1333
Расчетный критерий Фишера Fр= 1.7/ 0.1333 = 12.6
Табличный критерий Фишера Fт= 9.1 (число степеней свободы числителя 4, знаменателя 3 в таблице 3.2)
Поскольку Fp > FT уравнение регрессии можно использовать.
Результаты обработки данных в пакете Matlab 6.1 показан на рисунке 3.8
Рис. 3.8 Фрагмент окна в пакете Matlab 6.1