§ 4.1.2 Математическое обеспечение имитационного моделирования.

Математическое обеспечение имитационного моделирования базируется на 3-х разделах математики (рис. 4.2).

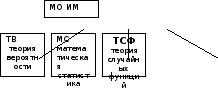
Рис. 4.2 Структура математического обеспечения имитационного моделирования

ТВ изучает случайные события. Напомним некоторые понятия, необходимые для понимания методики стохастического моделирования. Событие – всякий факт, который в результате опыта может произойти или не произойти. их три: достоверное, невозможное и вероятное. Физический процесс, в котором осуществляется и фиксируется наличие или отсутствие событий, называется опытом. Опыт проводится при строго определенных условиях. Событие, которое в определенных условиях:

• обязательно происходит, называют достоверным;

• не может произойти, называют невозможным;

• может произойти, но и не может произойти, называют случайным.

Числовую характеристику степени возможности появления события в тех или иных условиях, которые могут повторяться неограниченное число раз, называют вероятностью. Совокупность множества однородных событий составляют первоначальный статистический материал. Различают генеральную совокупность событий N (X) и её часть N₁(x), называемой выборочной совокупностью (малая выборка). Один из способов вычисления вероятности – отношение P{X} = p(x) = N₁(x)/ N (X).

Для достоверных событий p(x) = 1; для невозможных p(x) = 0, а для случайных справедливо равенство 0 ≤ p(x) ≤ 1.

Количественной характеристикой некоторых событий (например, измерение физической переменной) является случайная величина, которая в результате опыта принимает одно из возможных значений, заранее неизвестное.

Математическая статистика изучает способы обработки и анализа случайных величин. По аналогии вводят понятие – частота события y^*(x), представляющей собой отношение числа случаев, n(x) при которых случайная величина (СВ) x имела оно и тоже значение к общему числу случаев n..

y^*(x) = n(x) / n , причем при n → ∞ y^*(x) → P(x)

Вычислив частоту для разных значений y^*(x_i) можно построить гистограмму, график, где каждому значению x_i будет соответствовать y^*(x_i).

В результате опыта можно получить частоту случайных значений СВ. Случайная величина может принять любое значение. Функция распределения случайной величины – плавная кривая аппроксимирующая гистограмму.

Поскольку случайные величины могут быть дискретные и непрерывные, то различают два вида распределения Д функция распределения и U функция распределения.

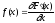
– плотность распределения

Рис. 4. 3 Равномерное распределение

Рис. 4.4. Нормальное распределение

Каждая случайная величина может быть охарактеризована случайными величинами: математическое ожидание, дисперсия, мода, медиана, асимметрия (скошенность), эксцесс (крутость).

Мода – это вероятность наибольшего значения случайной величины. Медиана – это вероятность среднего значения случайной величины. Симметрия, асимметрия и эксцесс вычисляются через так называемые моменты случайной величины, они бывают центральные и начальные.

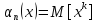–начальный момент

–центральный момент

Пусть выборка х = (3 , 4 , 5)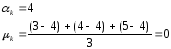

Второй центральный момент дисперсия.

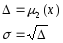
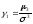
Асимметрия или

Эксцесс или крутость.

Регрессионный анализ – это получение коэффициента уравнения регрессий.

Дисперсионный анализ – сравнение распределений.

Как для дискретных, так и для непрерывных функций известны распределения.

Дискретные распределения: биноминальное, полиноминальное, Паскаля, Пуассона.

Непрерывные распределения: нормальное, логарифмически нормальное, Реллея, Максона, Симпсона, Коши, экспоненциальное , χ², Фишера.

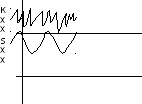
Теория случайных функций изучает случайные функции, которыми описываются случайные процессы. Если случайная функция реализована и записана во времени, то она перестает быть случайной, и её называют реализацией.

Если случайная величина описывается совокупностью случайных величин, то случайный процесс описывается набором реализаций случайных функций.

Рис. 4.5 Реализации случайного процесса

По всем реализациям можно оценить статистические характеристики.

В сечении функций мы получаем набор случайных величин, для которых можно вычислить все статистические характеристики. Если математическое ожидание для всех реализаций случайных процессов остается одинаковым, то это стационарный процесс.

Если статистические характеристики, вычисленные по всем реализациям, совпадают со статистическими характеристиками, вычисленными по одной реализации, то процесс называют эргодическим.

Для оценки в динамике используется корреляционные функции и спектральные плоскости.

t

ω

Корреляционная функция показывает связь между двумя соседними значениями случайной функции.

Спектральная плотность или функция отражают частотные характеристики процессов.

Корреляционная функции и спектральные плоскости связаны между собой через преобразование Фурье.

Случайная функция (центрированная функция) описывается функцией распределения и характеристиками.

Для вычисления СФ приходится проводить дискретизацию: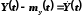

i = 1, 2, ...., n; v - номер реализации.

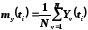
Для случайных процессов вычисляют еще две характеристики: корреляционную функцию и спектральную плотность: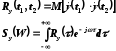

где  - сдвиг между t₁ и t₂.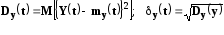

Различают случайные стационарные процессы, в которых m_y(t)=const, D_y(t)=const, a R_y(t₁, t₂)=R_y().

Эргодичные случайные процессы, в которых статистические характеристики, полученные осреднением во времени одной реализации (в достаточно большом интервале наблюдения), приближенно совпадают с характеристиками полученными осреднением по множеству реализаций (при фиксированном времени). Y(t) эргодична, если R_y(t) неограниченно убывает по модулю при  .