
big_doc_LKG
.pdf
130 |
Розділ 2 |
Розв’язок. Так як приклад є зразковим, то відійдемо від умови обчислення критерію за негрупованими вибірками, а скористаємося середніми інтервальними значеннями досліджуваної випадкової величини.
Маємо 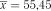 ,
,  . Значення функції нормального розподілу приймаємо за додатком Д1 у відповідності з оператором
. Значення функції нормального розподілу приймаємо за додатком Д1 у відповідності з оператором
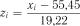 .
.
Результати розрахунку зводимо у таблицю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
15 |
|
–2,10 |
|
0,0179 |
|
0,11 |
|
0,00 |
|
0,0921 |
|
0,0179 |
|
2 |
25 |
|
–1,58 |
|
0,0571 |
|
0,22 |
|
0,11 |
|
0,1629 |
|
–0,0529 |
||
3 |
35 |
|
–1,06 |
|
0,1446 |
|
0,33 |
|
0,22 |
|
0,1854 |
|
–0,0754 |
||
4 |
45 |
|
–0,53 |
|
0,2981 |
|
0,43 |
|
0,33 |
|
0,1319 |
|
–0,0319 |
||
5 |
55 |
|
–0,02 |
|
0,4920 |
|
0,53 |
|
0,43 |
|
0,0380 |
|
0,0620 |
|
|
6 |
65 |
|
0,50 |
|
0,6915 |
|
0,63 |
|
0,53 |
|
-0,0615 |
|
0,1615 |
|
|
7 |
75 |
|
1,02 |
|
0,8461 |
|
0,73 |
|
0,63 |
|
-0,1161 |
|
0,2161 |
|
|
8 |
85 |
|
1,54 |
|
0,9382 |
|
0,83 |
|
0,73 |
|
-0,1081 |
|
0,2082 |
|
|
9 |
95 |
|
2,06 |
|
0,9803 |
|
0,93 |
|
0,83 |
|
-0,0503 |
|
0,1503 |
|
|
|
Із таблиці виходить |
; |
|
; |
|
|
|
. |
|||||||
За формулою |
(2.16) |
розраховуємо |
критичне |
значення |
статистики |
. Маємо |
|||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
 .
.
Так як 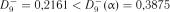 , то гіпотеза
, то гіпотеза  про нормальність розпо-
про нормальність розпо-
ділу випадкової величини підтверджується.
За формулою (2.17) знайдемо перетворену статистику
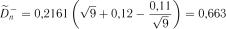 .
.
Критичне значення статистики  . Так як
. Так як 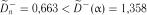 , нульова гіпотеза
, нульова гіпотеза  про нормальний розподіл випадкової величини також підтвер-
про нормальний розподіл випадкової величини також підтвер-
джується.
Критерій Купера. Заснований на розширеній статистиці критерію Колмогорова-Смірнова

Ідентифікація параметрів статистичними законами розподілу |
131 |
.
Статистика критерію розраховується за формулою
, |
(2.18) |
де  ,
, 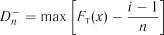 .
.
До граничного розподілу швидко збігається модифікована форма статистики критерію:
для верхніх процентних точок
; (2.19)
для нижніх процентних точок
. (2.20)
Критичне значення для верхніх процентних точок на рівні значимості 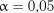 дорівнює
дорівнює  . При
. При 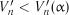 нульова гіпотеза підтверджується.
нульова гіпотеза підтверджується.
Приклад 6. В умовах прикладу 1 перевірити гіпотезу нормальності розподілу на рівні значимості 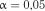 .
.
Розв’язок. При розв’язанні прикладу 4 були отримані значення 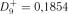 та
та 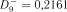 . Звідки
. Звідки 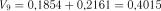 або в модифікованій формі для верхніх процентних точок за формулою (2.19):
або в модифікованій формі для верхніх процентних точок за формулою (2.19):
.
Оскільки 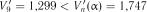 нульова гіпотеза про нормальність розпо-
нульова гіпотеза про нормальність розпо-
ділу підтверджується.
132 |
Розділ 2 |
2.4.2. Спеціальні критерії для перевірки розподілу. Спеціальні критерії застосовуються для конкретних видів розподілу і враховують їх специфіку. Для нормального розподілу застосування спеціальних критеріїв викладено в розділі 1.3.2.
2.4.2.1. Критерії перевірки експоненціальності розподілу. Перш ніж проводити перевірку, необхідно впевнитися у тому, що імовірнісна поведінка випадкової величини за своєю фізичною сутністю підпорядковується «бажаному» експоненціальному закону (наприклад, тривалість обслуговування, моменти надходження транспортних засобів на вантажний пункт тощо). Розглянемо найбільш прийнятні для практичного використання критерії.
Критерій Шапіро–Уілка. Для вибірки  розг-
розг-
лядається щільність імовірностей
(2.21)
з невідомим параметром  . Тоді статистика критерію має вигляд
. Тоді статистика критерію має вигляд
, |
(2.22) |
або при 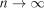 (
( )
)
. (2.23)
Гіпотеза експоненціальності спостережного розподілу підтверджується на рівні значимості  , якщо
, якщо 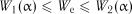 де
де 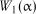 і
і 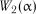 – критичні значення критерію, наведені в табл. 2.6.
– критичні значення критерію, наведені в табл. 2.6.
Таблиця 2.6
Критичні значення критерію  на рівні значимості
на рівні значимості
|
|
Ідентифікація параметрів статистичними законами розподілу |
133 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0,062 |
0,404 |
|
15 |
0,036 |
0,163 |
|
23 |
0,022 |
0,087 |
|
31 |
0,017 |
|
0,057 |
|
8 |
0,054 |
0,342 |
16 |
0,034 |
0,150 |
24 |
0,021 |
0,082 |
32 |
0,017 |
|
0,055 |
|
||||
9 |
0,050 |
0,301 |
17 |
0,030 |
0,135 |
25 |
0,021 |
0,078 |
33 |
0,017 |
|
0,053 |
|
||||
10 |
0,049 |
0,261 |
18 |
0,028 |
0,123 |
26 |
0,020 |
0,073 |
34 |
0,017 |
|
0,057 |
|
||||
11 |
0,046 |
0,234 |
19 |
0,026 |
0,114 |
27 |
0,020 |
0,070 |
35 |
0,016 |
|
0,049 |
|
||||
12 |
0,044 |
0,215 |
20 |
0,025 |
0,106 |
28 |
0,019 |
0,067 |
|
|
|
|
|
|
|||
13 |
0,040 |
0,195 |
21 |
0,024 |
0,101 |
29 |
0,019 |
0,064 |
|
|
|
|
|
|
|||
14 |
0,038 |
0,178 |
22 |
0,023 |
0,094 |
30 |
0,018 |
0,060 |
|
|
|
|
|
|
|||
Приклад 7. Статистичні дані про тривалість (в годинах) розвантаження вагонів з дрібнопартіонними вантажами представлені вибіркою
 : 0,5; 0,8; 1,1; 1,6; 2,0; 2,4; 3,2; 3,8; 4,3; 4,6; 5,0; 7,5; 8,2; 9,6; 10,6.
: 0,5; 0,8; 1,1; 1,6; 2,0; 2,4; 3,2; 3,8; 4,3; 4,6; 5,0; 7,5; 8,2; 9,6; 10,6.
Перевірити відповідність розподілу імовірностей тривалості розвантаження експоненціальному розподілу на рівні значимості 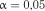 .
.
Розв’язок. Обчислюємо величини
; |
; |
. |
За формулою (2.19) визначаємо 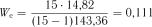 .
.
За табл. 2.6 для 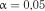 і
і  знаходимо
знаходимо 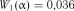 і
і  . Так як
. Так як 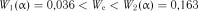 , гіпотеза експоненціальності розподілу тривалості розвантаження вагонів відхиляється.
, гіпотеза експоненціальності розподілу тривалості розвантаження вагонів відхиляється.
Критерії типу Колмогорова-Смірнова. Гіпотетичний закон розподілу має вигляд
, |
|
|
де і – невідомі параметри. |
|
|
Оцінки параметрів за ранжованою вибіркою |
|
|
отримують за формулами |
|
|
; |
. |
(2.24) |

134 |
Розділ 2 |
Позначивши  , переходимо до нормованого експоненці-
, переходимо до нормованого експоненці-
ального розподілу  , для якого можна використати різні статистики критеріїв згоди.
, для якого можна використати різні статистики критеріїв згоди.
Критерій Колмогорова-Смірнова.
; |
; |
(2.25) |
 .
.
Значення статистики розраховується за формулою
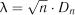 . (2.26)
. (2.26)
Обчислене значення порівнюється з критичним 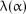 .
.
Критерій 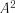
|
. |
(2.27) |
Критерій |
|
|
|
. |
(2.28) |
Критерій |
|
|
, де |
. |
(2.29) |
Критерій |
|
|
|
. |
(2.30) |
Статистика критерію розраховується за формулою
 . (2.31)
. (2.31)
Критичні значення статистик на рівні значимості 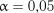 наведені у табл. 2.7.
наведені у табл. 2.7.
Таблиця 2.7 Критичні значення статистик критеріїв на рівні значимості 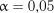
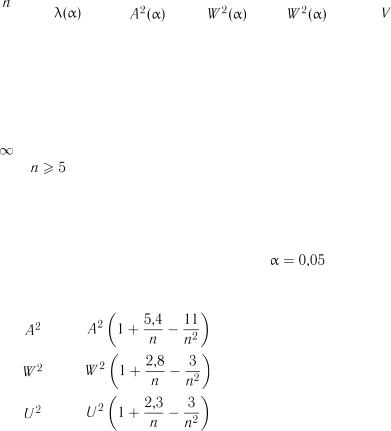
|
Ідентифікація параметрів статистичними законами розподілу |
135 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Критерії |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,865 |
0,725 |
0,141 |
0,113 |
1,314 |
|
|
10 |
0,977 |
0,920 |
0,176 |
0,131 |
1,461 |
|
|
|
15 |
1,002 |
1,009 |
0,188 |
0,139 |
1,504 |
|
|
|
20 |
1,021 |
1,062 |
0,195 |
0,143 |
1,536 |
|
|
|
25 |
1,033 |
1,097 |
0,199 |
0,146 |
1,559 |
|
|
|
500 |
1,061 |
1,197 |
0,209 |
0,152 |
1,600 |
|
|
|
100 |
1,072 |
1,250 |
0,215 |
0,155 |
1,647 |
|
|
|
|
|
1,094 |
1,321 |
0,222 |
0,159 |
1,656 |
|
|
|
Для |
верхні |
процентні |
точки розподілу |
статистик цілком спів- |
|||
падають з граничними розподілами при використанні модифікацій, наведених в табл. 2.8.
|
|
|
|
|
Таблиця 2.8 |
|
|
Процентні точки модифікованих критеріїв |
|||||
|
|
типу Колмогорова-Смірнова ( |
) |
|
|
|
|
|
|
|
|
|
|
Статистика |
|
Модифікація |
Процентні |
|
№ формули |
|
|
точки |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,321 |
|
(2.32) |
|
|
|
|
0,222 |
|
(2.33) |
|
|
|
|
0,159 |
|
(2.34) |
|
|
|
|
|
|
|
|
Приклад 8. Маємо 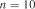 спостережень інтервалів
спостережень інтервалів  (у хвилинах) прибуття автомобілів на вантажний пункт:
(у хвилинах) прибуття автомобілів на вантажний пункт:
 : 1, 2, 4, 5, 9, 11, 18, 21, 29, 35.
: 1, 2, 4, 5, 9, 11, 18, 21, 29, 35.
Перевірити можливість опису транспортного потоку експоненціальним законом розподілу на рівні значимості 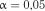 .
.
Розв’язок. Обчислюємо за формулами (2.24) величини  і
і 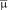 :
:

136 |
Розділ 2 |
; |
|
; |
. |
Обчислюємо величини |
і |
: |
|
|
|
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
; |
. |
|
|
Виконуємо перевірку за різними критеріями.
Критерій Колмогорова-Смірнова. Результати розрахунку представлені у таблиці.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,1 |
0,0952 |
0,0048 |
|
0,0 |
0,0952 |
|
2 |
0,2 |
0,1580 |
0,0420 |
|
0,1 |
0,0580 |
|
|
3 |
0,3 |
0,2709 |
0,0291 |
|
0,2 |
0,0709 |
|
|
4 |
0,4 |
0,3216 |
0,0784 |
|
0,3 |
0,0216 |
|
|
5 |
0,5 |
0,4913 |
0,0087 |
|
0,4 |
0,0913 |
|
|
6 |
0,6 |
0,5596 |
0,0404 |
|
0,5 |
0,0956 |
|
|
7 |
0,7 |
0,7339 |
–0,0339 |
|
0,6 |
0,1339 |
|
|
8 |
0,8 |
0,7856 |
0,0144 |
|
0,7 |
0,0856 |
|
|
9 |
0,9 |
0,8795 |
0,0205 |
|
0,8 |
0,0795 |
|
|
10 |
1,0 |
0,9218 |
0,0782 |
|
0,9 |
0,0218 |
|
|
Із таблиці маємо: |
|
|
, |
|
; |
|||
|
|
|
. |
|
|
|
|
|
Значення статистики критерію за формулою (2.26) дорівнює
.
Із табл. 2.7 для 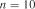 знаходимо
знаходимо 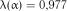 . Так як
. Так як 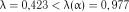 , гіпотеза експоненціальності розподілу величини
, гіпотеза експоненціальності розподілу величини  підтверджується.
підтверджується.
Критерій 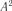 . Обчислюємо за формулою (2.27):
. Обчислюємо за формулою (2.27):

Ідентифікація параметрів статистичними законами розподілу |
137 |
Із табл. 2.7 для  знаходимо критичне значення
знаходимо критичне значення 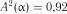 . Для модифікованого критерію маємо (2.32):
. Для модифікованого критерію маємо (2.32):
.
Критичне значення із табл. 2.8 дорівнює 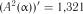 . Таким чином, маємо:
. Таким чином, маємо: 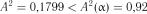 та
та 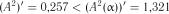 , отже, гіпотеза про експоненціальність розподілу величини
, отже, гіпотеза про експоненціальність розподілу величини  підтверджується.
підтверджується.
Критерій 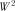 . Обчислюємо статистики критерію за формулами (2.28) і (2.33):
. Обчислюємо статистики критерію за формулами (2.28) і (2.33):
|
. |
|
Критичні значення статистики для дорівнюють |
(табл. 2.7) |
|
та |
(табл. 2.8). Таким чином, маємо |
|
та |
, тобто, гіпотеза експоненціальності розподілу |
|
величини |
підтверджується. |
|
138 |
Розділ 2 |
Критерій 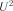 . Обчислюємо
. Обчислюємо 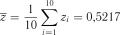 . За формулами (2.29), (2.34)
. За формулами (2.29), (2.34)
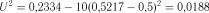 ;
; 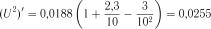 .
.
Із табл. 2.7 для 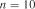 знаходимо
знаходимо 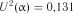 , із табл. 2.8 —
, із табл. 2.8 — 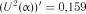 . Так як
. Так як 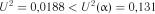 і
і 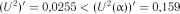 , то гіпотеза експоненціальності розподілу величини
, то гіпотеза експоненціальності розподілу величини  підтверджується.
підтверджується.
Критерій  . Маємо:
. Маємо: 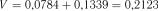 ;
; 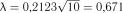 . Із табл. 2.7 для
. Із табл. 2.7 для  визначаємо критичне значення статистики
визначаємо критичне значення статистики 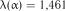 . Так як
. Так як 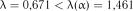 , то гіпотеза експоненціальності розподілу величини
, то гіпотеза експоненціальності розподілу величини  під-
під-
тверджується.
Критерій Фроціні. Статистика критерію обчислюється за формулою
. (2.35)
Критичні значення 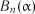 наведені у табл. 2.9.
наведені у табл. 2.9.
Таблиця 2.9
Критичні значення критерію 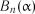 для
для 
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,3687 |
11 |
0,3790 |
17 |
0,3806 |
6 |
0,3666 |
12 |
0,3784 |
18 |
0,3814 |
7 |
0,3742 |
13 |
0,3768 |
19 |
0,3844 |
8 |
0,3740 |
14 |
0,3821 |
20 |
0,3795 |
9 |
0,3800 |
15 |
0,3837 |
|
0,3840 |
10 |
0,3820 |
16 |
0,3777 |
|
|
|
|
|
|
|
|
При 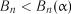 нульова гіпотеза
нульова гіпотеза 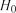 підтверджується.
підтверджується.
Приклад 9. В умовах прикладу 8 перевірити гіпотезу експоненціальності даних на рівні значимості 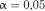 .
.
Розв’язок. При 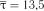 обчислюємо статистику
обчислюємо статистику

Ідентифікація параметрів статистичними законами розподілу |
139 |
Із табл. 2.9 для  знаходимо
знаходимо 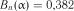 . Порівнюючи фактичне і критичне значення, маємо
. Порівнюючи фактичне і критичне значення, маємо 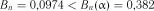 . Отже, гіпотеза експоненціальності розподілу величини
. Отже, гіпотеза експоненціальності розподілу величини  підтверджується.
підтверджується.
До окремої групи слід віднести критерії, побудовані на твердженні сталості інтенсивності відмов деякого виробу у часі. Припускається перевірка гіпотези  (сталість інтенсивності відмов) проти альтернативи монотонної зміни інтенсивності відмов.
(сталість інтенсивності відмов) проти альтернативи монотонної зміни інтенсивності відмов.
В теорії транспортних систем такий підхід можна розповсюдити на перевірку експоненціальності розподілу деяких характерних показників транспортного процесу:
–інтенсивності відмов в обслуговуванні клієнтів;
–інтенсивності потоку замовлень на транспортне обслуговування;
–інтенсивності поповнення складських запасів;
–ступенів використання транспортних засобів, складського обладнання, засобів механізації, які характеризується інтенсивністю
попиту на них тощо.
Для практичного використання можна рекомендувати такі наступні порівняно прості в обчислені критерії.
Критерій Кочара. Застосовується для перевірки сталості відмови в обслуговуванні або замовлення на обслуговування проти альтернативи їх монотонного зростання. Статистика критерію для ранжованого за зростанням ряду 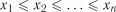 має вигляд
має вигляд
, |
(2.36) |
де  .
.
