
big_doc_LKG
.pdfВипадкові процеси та їх статистичні характеристики |
189 |
Стан системи характеризується векторами наступного вигляду

|
|
|
|
|
|
|
|
|
|
|
Таблиця 3.15 |
|
|
|
|
Розрахунок складових для обчислення критерію |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реалізація (доба) |
|
Значення параметра (чисельник) і його ранг (знаменник) погодинно |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сума рангів |
60 |
60,5 |
50,5 |
24 |
50,5 |
55,5 |
29 |
47,5 |
42,5 |
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
20,2 |
16,8 |
8 |
16,8 |
18,5 |
9,7 |
15,8 |
14,1 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,5 |
4,7 |
1,3 |
–7,5 |
1,3 |
3 |
–5,8 |
0,3 |
–0,4 |
–0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20,25 |
22,09 |
1,69 |
56,25 |
1,69 |
9 |
33,64 |
0,09 |
1,96 |
0,25 |
146,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Випадкові процеси та їх статистичні характеристики |
191 |
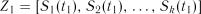 ;
;
 ;
;
.....................................................
 .
.
Якщо розглядати поведінку системи як послідовну зміну станів 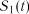 ,
, 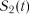 , ...,
, ..., 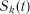 , то їх можна інтерпретувати як координати точки у k-вимірному фазовому просторі, причому кожній реалізації процесу відповідає певна фазова траєкторія. Сукупність всіх можливих значень станів {S} називається простором станів досліджуваного об’єкта.
, то їх можна інтерпретувати як координати точки у k-вимірному фазовому просторі, причому кожній реалізації процесу відповідає певна фазова траєкторія. Сукупність всіх можливих значень станів {S} називається простором станів досліджуваного об’єкта.
Для опису поведінки систем при наявності випадкових факторів широко використовується математичний апарат марківських випадкових процесів. Із всієї множини марківських випадкових процесів розглядаються тільки процеси із скінченою або ліченою множиною станів.
Нехай маємо дискретний випадковий процес, який відбувається в системі з можливими станами  ,
, 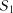 ,
, 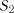 , ...,
, ...,  , ...,
, ..., 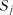 . Позначимо
. Позначимо
умовну імовірність того, що в момент  система буде у стані
система буде у стані
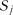 , якщо в момент
, якщо в момент 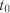 вона була у стані
вона була у стані  , через
, через  . Дискретний
. Дискретний
випадковий процес функціонування системи називається марківським, якщо імовірність 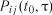 залежить тільки від вказаних в позначенні
залежить тільки від вказаних в позначенні
параметрів  ,
,  ,
, 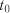 ,
,  , тобто від того, у якому стані була система у момент
, тобто від того, у якому стані була система у момент 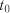 і в який стан вона може перейти через інтервал часу
і в який стан вона може перейти через інтервал часу  .
.
Розрізняють два основних види марківських випадкових процесів:
1)з дискретним станом і дискретним часом;
2)з дискретним станом і неперервним часом.
Випадковий процес називається процесом з дискретним станом, якщо можливі стани системи  ,
,  ,
, 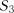 , ... можна перелічити (перенумерувати) один за іншим, а безпосередньо процес полягає у тому, що час від часу система
, ... можна перелічити (перенумерувати) один за іншим, а безпосередньо процес полягає у тому, що час від часу система  стрибком (миттєво) переходить із одного стану в інший.
стрибком (миттєво) переходить із одного стану в інший.
Марківським випадковим процесом з дискретним часом називається процес, у якому переходи із одного стану в інший можливі тільки у певні фіксовані моменти часу.
Марківським випадковим процесом з неперервним часом називається процес, у якого перехід із одного стану в інший відбувається в будь які випадкові моменти часу.
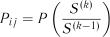
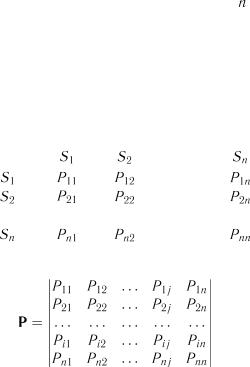
Випадкові процеси та їх статистичні характеристики |
193 |
|
Оскільки система може перебувати в одному із |
станів, то для |
|
формалізації процесу в кожний момент часу 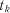 необхідно задати
необхідно задати 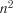 імовірностей переходів
імовірностей переходів  . Формалізовану модель процесу можна представити у вигляді таблиці (табл. 3.16) або матриці (3.21).
. Формалізовану модель процесу можна представити у вигляді таблиці (табл. 3.16) або матриці (3.21).
Таблиця 3.16 Перехідні ймовірності системи
Стан |
|
|
Стан |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
… |
… |
… |
|
… |
… |
|
|
|
|
… |
|
, (3.21)
де 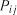 – імовірність переходу системи за один крок із стану
– імовірність переходу системи за один крок із стану  до стану
до стану 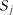 ;
;
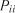 – імовірність затримки системи в стані
– імовірність затримки системи в стані 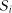 .
.
Матриця (3.21) називається перехідною, або матрицею перехід-
них ймовірностей. Відзначимо деякі особливості цієї матриці:
1)кожний рядок характеризує вибраний стан системи, а його елементами є імовірності можливих переходів системи за один крок із вибраного (і-го) стану, у тому числі і перехід в саму себе;
2)елементи стовпців показують імовірності всіх можливих переходів системи за один крок в заданий (ј-й) стан (інакше кажучи, рядок характеризує імовірність переходу системи із стану, а стовпець – до стану);
3)сума ймовірностей кожного рядка дорівнює одиниці, так як переходи утворюють повну групу подій;
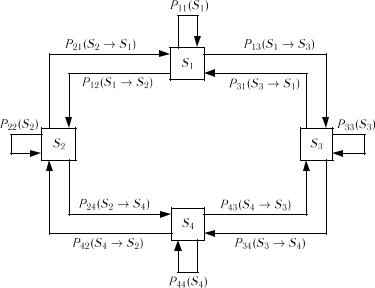

Випадкові процеси та їх статистичні характеристики |
195 |
Один із них полягає у тому, що поведінка великої кількості окремих елементів системи (автомобілі, вантажні пункти, перевізні документи, види вантажів тощо) розглядається за окремі періоди часу  (година, зміна, день) протягом відповідно невеликого періоду функціонування системи (зміна, доба, тиждень, місяць).
(година, зміна, день) протягом відповідно невеликого періоду функціонування системи (зміна, доба, тиждень, місяць).
Другий спосіб передбачає вивчення окремо вибраного елемента системи протягом достатньо великого періоду часу T (наприклад, дослідження роботи вантажних пунктів, окремих дільниць складів, наван- тажувально-розвантажувальних машин, транспортних засобів i т.д. періодами часу  , що дорівнюють одній годині, дню, впродовж декількох місяців, років).
, що дорівнюють одній годині, дню, впродовж декількох місяців, років).
За фіксованими показниками стану при дослідженні систем можна визначити:
1)кількість переходів системи із одного стану до іншого;
2)кількість появ тих чи інших ознак в окремі періоди 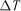 функціо-
функціо-
нування системи (наприклад, кількість показників в різноманітних формах документів; кількість видів перероблюваних вантажів; кількість транспортних засобів, які прибувають на вантажний пункт тощо).
На підставі проведених досліджень визначається зведена матриця показників
. (3.22)
Надалі розраховують суму значень показників по кожному рядку. Поділивши кожний елемент рядка на відповідну суму показників у цьому рядку, отримаємо основну матрицю (3.21) перехідних ймовірностей.
Використовуючи матрицю (3.21) можна визначити ймовірності станів  системи після k-го кроку переходів за рекурентною формулою
системи після k-го кроку переходів за рекурентною формулою
( ), (3.23)
), (3.23)
де |
– можлива кількість станів системи; |
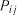

Випадкові процеси та їх статистичні характеристики |
197 |
Із табл. 3.17 виходить, що протягом місяця перший автомобіль (перший рядок табл. 3.17) 3 дні (з 1-го по 3-й день місяця) працював на лінії (Л), потім один день (4- й) знаходився на технічному ремонті (Р), з 5-го по 13-й день місяця працював на лінії, в 14-й проходив технічне обслуговування ТО-1 (1), з 15-го по 19-й день на лінії, 20-й день на ТО-1, 21-й - 23-й – на лінії, 24-й – на ТО-1, з 25-го по 31-й – на лінії і т.д. Аналогічно восьмий автомобіль 1-й та 2-й дні поточного місяця перебував на лінії, на 3-й день знаходився у парку (резерві), з 4-го по 9-й – на лінії і т. д.
Матриця перехідних імовірностей має вигляд
.
Використовуючи інформацію табл. 3.17 як вихідні дані, визначимо загальну кількість переходів цих автомобілів із п’яти станів (Л); (1); (Р); (2); (П) в ті ж самі стани. Для цього підготуємо табл. 3.18, в якій по горизонталі і вертикалі зазначені відповідні стани системи (Л); (1); (Р); (2); (П).
|
|
|
|
|
|
Таблиця 3.18 |
|
Підсумкові дані про кількість переходів в різні технологічні стани |
|||||
|
|
|
|
|
|
|
Стани |
|
|
|
Стани |
|
|
|
|
|
|
|
|
|
|
Л (лінія) |
1 (ТО-1) |
Р (ТР) |
2 (ТО-2) |
П (парк) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+8+4+2+ |
1+1+1+1 |
1+1+1+ |
1+1+1+1 |
1+1+1+1 |
|
|
9+8+8+15 |
+1+1+1+ |
1+1+1+ |
|
+1 |
|
|
+4+5+9+4 |
1+1+1+1 |
1+1+1 |
|
|
Л |
|
+8+13+7+ |
+1+1+1+ |
|
|
|
|
5+6+6+5+ |
1+1+1+1 |
|
|
|
|
(лінія) |
|
7+13+8+7 |
+1+1 |
|
|
|
|
|
+2+5+3+3 |
|
|
|
|
|
|
+7+2+2+1 |
|
|
|
|
|
|
1+8+11+2 |
|
|
|
|
|
|
+2+3 |
|
|
|
|
1 |
|
21 |
– |
– |
– |
1 |
(ТО-1) |
|
|||||
|
|
|
|
|
|
|
Р |
|
8 |
1 |
2 |
– |
– |
(ТР) |
|
|||||
|
|
|
|
|
|
|
2 |
|
2 |
1 |
– |
2 |
1 |
(ТО-2) |
|
|||||
|
|
|
|
|
|
|
П |
|
7 |
– |
– |
– |
1 |
(парк) |
|
|||||
|
|
|
|
|
|
|


 ,
, 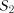 , ...,
, ..., 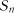 , для якої переходи із стану в стан можливі тільки в дискретні моменти часу
, для якої переходи із стану в стан можливі тільки в дискретні моменти часу  ,
, 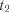 , ...,
, ..., 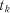 , ...,
, ..., 
 ,
, 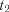 , ...,
, ..., 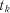 існують деякі імовірності переходу системи із одного стану в будь-який інший, а також імовірності перебування (затримки) системи у даному стані. Ці імовірності на-
існують деякі імовірності переходу системи із одного стану в будь-який інший, а також імовірності перебування (затримки) системи у даному стані. Ці імовірності на- ,
, 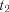 , ... система переходить в інший стан (або залишається у попередньому) випадково (наприклад,
, ... система переходить в інший стан (або залишається у попередньому) випадково (наприклад, 
 i т.д.).
i т.д.).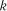 моментів часу (кроків) у стані
моментів часу (кроків) у стані  через
через 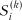 , а імовірності цих подій після
, а імовірності цих подій після  -го кроку як
-го кроку як ;
;  ; ... ;
; ... ; 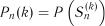 .
. ,
, 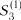 ,
, 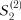 ,
, 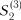 ,
, 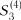 , ...
, ...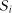 в будь-який стан
в будь-який стан 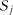
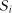 . Найважливішою особливістю марківського ланцюга є те, що перехід системи у наступні моменти в деякий стан залежить тільки від стану, у якому вона була в даний момент.
. Найважливішою особливістю марківського ланцюга є те, що перехід системи у наступні моменти в деякий стан залежить тільки від стану, у якому вона була в даний момент.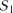 ,
, 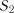 , ...,
, ..., 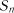 в момент часу
в момент часу 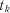 характеризують умовними ймовірностями
характеризують умовними ймовірностями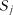 за умови, що в момент часу
за умови, що в момент часу  вона знаходилась у стані
вона знаходилась у стані 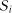 .
.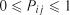 , а
, а  .
.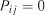 означає, що перехід за один крок із
означає, що перехід за один крок із  того, що система не вийде із стану
того, що система не вийде із стану  , а залишиться в ньому.
, а залишиться в ньому.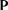 можна будувати декількома способами.
можна будувати декількома способами. –імовірність перебування системи в
–імовірність перебування системи в  за дискретними періодами часу
за дискретними періодами часу 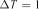 доба. Зафіксовані за часом
доба. Зафіксовані за часом  стани 10 автомобілів КАМАЗ–5320 протягом періоду часу
стани 10 автомобілів КАМАЗ–5320 протягом періоду часу 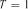 місяць (31 день) наведені в табл. 3.17.
місяць (31 день) наведені в табл. 3.17. для декількох періодів
для декількох періодів 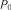 автомобілів для п’яти станів, використовуючи звітні дані АТП за розглядуваний період часу (1 місяць). Для цього кількість днів роботи усіх автомобілів на лінії, а також їх перебування відповідно на ТО-1, ТР, ТО-2 і в резерві розділимо на їх сумарну кількість.
автомобілів для п’яти станів, використовуючи звітні дані АТП за розглядуваний період часу (1 місяць). Для цього кількість днів роботи усіх автомобілів на лінії, а також їх перебування відповідно на ТО-1, ТР, ТО-2 і в резерві розділимо на їх сумарну кількість.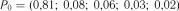 .
.