
big_doc_LKG
.pdf
Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 289
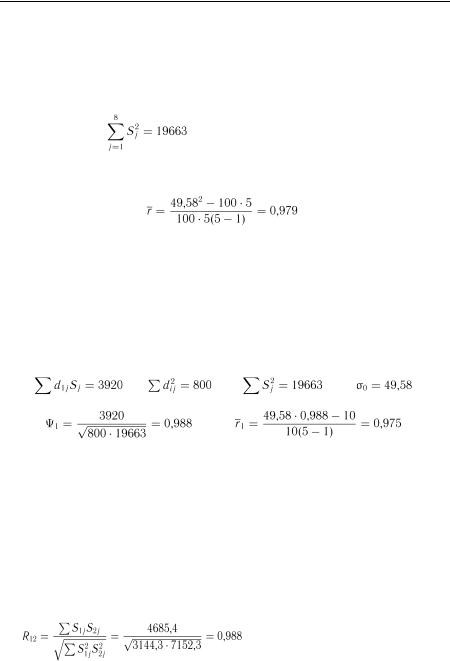
Так як значення коефіцієнтів дисгармонічності  є достатньо малими, і коефіцієнти кореляції
є достатньо малими, і коефіцієнти кореляції  є додатними, то можна об’єднати дві випадкові кореляційні оцінки в одну загальну комплексну оцінку
є додатними, то можна об’єднати дві випадкові кореляційні оцінки в одну загальну комплексну оцінку  .
.
2. Оцінка ступеня зв’язку між факторами всередині комплексу. Для обчислення внутрішньокомплексного коефіцієнта кореляції (5.58) розраховуємо величини:
; .
.
Для кількості факторів  коефіцієнт кореляції дорівнює
коефіцієнт кореляції дорівнює
.
Так як  , то сукупність вважається однорідною. Обчислюємо похибку внутрішньокомплексного коефіцієнта кореляції (5.59)
, то сукупність вважається однорідною. Обчислюємо похибку внутрішньокомплексного коефіцієнта кореляції (5.59)
 .
.
3. Обчислення групових коефіцієнтів кореляції. Розглядаємо першу ознаку.
Маємо:
; |
; |
; |
; |
|
; |
|
. |
Для решти факторів аналогічним чином отримані такі значення коефіцієнтів кореляції:  ;
;  ;
;  ;
;  . Всі групові коефіцієнти кореляції за величиною є великими і не підлягають виключенню зі статистичного комплексу.
. Всі групові коефіцієнти кореляції за величиною є великими і не підлягають виключенню зі статистичного комплексу.
4. Обчислення міжкомплексного коефіцієнту кореляції. Використовуємо формулу (5.63). Поділяємо весь комплекс на дві частини. В перший підкомплекс входять фактори  та
та  . До другого підкомплексу входять фактори
. До другого підкомплексу входять фактори  ,
,  та
та  .
.
За вихідними даними (табл. 5.25) обчислюємо складові формули (5.63):
 ;
;  ;
;
.  .
.


Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 291
9.Охарактеризуйте функціональний, кореляційний і скедастичний зв’язки між ознаками.
10.За яким критерієм оцінюється надійність парного коефіцієнта кореляції?
11.Як можна виявити наявність кореляційної залежності між досліджуваними ознаками?
12.Що характеризує коефіцієнт частинної кореляції?
13.Яким чином розв’язується задача визначення щільності зв`язку у багатофакторному кореляційному аналізі?
14.У чому полягає сутність кореляційного аналізу
15.З якою метою здійснюється систематизація статистичного матеріалу за однією якісною ознакою?
16.Як формується задача при використані для дослідження методів парної кореляції?
17.Дайте визначення коефіцієнту детермінації.
18.Сформулюйте задачу і наведіть математичну модель задачі дослідження процесу функціонування систем методом множинної кореляції.
19.Назвіть способи перевірки правильності прийнятої гіпотези щодо прямолінійної форми кореляційного зв’язку.
20.Як можна оцінити «слабкий», «середній», «сильний» кореля-
ційні зв’язки?
21.Як визначається відсутність кореляційного зв’язку?
22.Як визначається наявність функціонального зв’язку?
23.Поясніть особливості аналізу статистичних даних з неоднорідними ознаками.
24.Що являє собою таблиця спряженості?
25.Наведіть таблицю спряженості для двох ознак і охарактеризуйте її складові.
26.Яка статистика використовується для оцінки зв’язку в статистичних комплексах з багатьма ознаками?
27.Наведіть формулу для обчислення коефіцієнту спряженості.
28.Що являє собою коефіцієнт точково-серійної кореляції?
29.Що характеризує метод дисгармонічних оцінок статистичного комплексу?
30.Що являє собою децисігмальна оцінка фактору?
31.Що визначає нормуючий децисігмальний коефіцієнт?
32.Наведіть і поясніть формулу стандартного відхилення децисігмальних оцінок.
РОЗДІЛ 6
АПРОКСИМАЦІЯ СТОХАСТИЧНИХ ЗВ'ЯЗКІВ ОДНОФАКТОРНИМИ РЕГРЕСІЙНИМИ МОДЕЛЯМИ
Мета вивчення теми – оволодіти методикою дослідження тран- спортно-технологічних процесів за допомогою однофакторного регресійного аналізу в умовах пасивного експерименту.
Після вивчення теми ви повинні вміти:
–виявляти в конкретних умовах діючого виробництва залежні і незалежні змінні;
–виконувати попереднє опрацювання зібраних статистичних даних;
–проводити змістовний аналіз факторних і результативних ознак;
–будувати емпіричні регресійні залежності;
–практично користуватися методикою однофакторного регресійного аналізу на ЕОМ з застосуванням стандартних програм;
–кількісно оцінювати параметри моделі та її адекватність;
–вибирати із множин альтернативних моделей раціональну для практичного використання.
6.1. Сутність регресійного аналізу
Задача полягає у визначенні кривої або поверхні, які дають най-
краще наближення до статистичних даних спостережень, без врахування флуктуацій (коливань). Відповідні методи наближення називаються регресійними. За допомогою цих методів розглядаються залежності між випадковими і невипадковими величинами. Такі залежності називаються регресійними, а моделі, за допомогою яких вони вивчаються – регресійними моделями. За функцію в регресійній мо-
делі обов’язково приймається випадкова величина (змінна)  , а за
, а за
аргумент – невипадкова величина  .
.
За допомогою регресійного аналізу визначають кількісну оцінку зв’язку між  та
та  у вигляді лінії регресії. Цей процес називається вирівнюванням емпіричної лінії регресії і включає такі процедури:
у вигляді лінії регресії. Цей процес називається вирівнюванням емпіричної лінії регресії і включає такі процедури:
–вибір виду рівняння зв’язку;
–ідентифікацію параметрів рівняння;
–визначення імовірності рівняння зв’язку.

|
Апроксимація зв’язків однофакторними регресійними моделями |
295 |
||||||||
де |
|
– фактичне значення досліджуваної ознаки; |
|
|
||||||
|
|
– теоретичне значення досліджуваної ознаки. |
|
|
||||||
Отримана таким чином регресійна модель перевіряється на відпо- |
||||||||||
відність експериментальним даним. |
|
|
|
|||||||
|
|
6.2. Методика складання рівнянь парної регресії |
|
|
||||||
Для побудови рівняння регресії повинні бути наявні не менш ніж |
||||||||||
20–25 спостережень. Розробка регресійної моделі проводиться у пос- |
||||||||||
лідовності, викладеній нижче. |
|
|
|
|
|
|||||
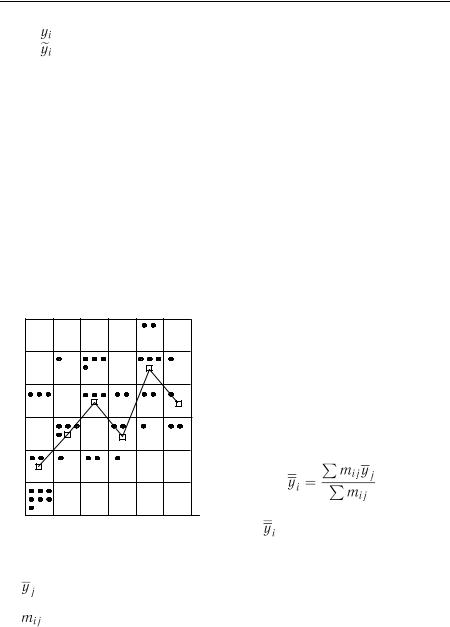
6.2.1. Встановлення форми лінії зв’язку (лінії регресії). Форму |
||||||||||
зв’язку можна встановити візуально, виходячи із графічного зобра- |
||||||||||
ження емпіричної лінії регресії (графіка ескізної функції). Побудову |
||||||||||
емпіричної лінії регресії здійснюють на підставі побудови поля коре- |
||||||||||
|
|
|
|
|
|
|
ляції і |
кореляційної таблиці. |
|
|
y |
|
|
|
|
|
|
Нехай, в результаті збирання |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
статистичного матеріалу |
було |
по- |
|
50 |
|
|
|
|
|
|
будоване поле кореляції (рис. 6.1) і |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
складена кореляційна таблиця. |
За |
||
40 |
|
|
|
|
|
|
даними кореляційної таблиці роз- |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
раховують середні значення у для |
|||
30 |
|
|
|
|
|
|
кожного інтервалу ознаки х за фо- |
|||
|
|
|
|
|
|
|
||||
20 |
|
|
|
|
|
|
рмулою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
, |
(6.3) |
|
0 |
2 |
4 |
6 |
8 |
10 |
x |
де |
– середнє значення |
ре- |
|
|
|
|
|
|
|
|
||||
Рис. 6.1. Емпірична лінія регресії |
|
зультативної ознаки в і-му стовпці |
||||||||
|
|
|
|
|
|
|
кореляційної таблиці; |
|
|
|
–середнє значення результативної ознаки в j-му інтервалі (по рядках);
–абсолютні частоти (кількість точок) ознаки у в клітині, утвореної і-м стовпцем і j-м рядком.
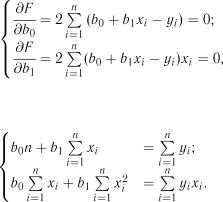
Апроксимація зв’язків однофакторними регресійними моделями |
297 |
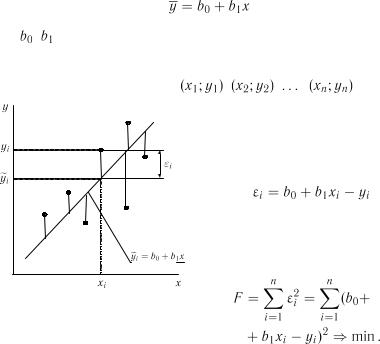
Невідомими величинами у цьому рівнянні будуть коефіцієнти  та
та  . Умови мінімізації функції (6.6) двох змінних за рівністю нулю частинних похідних по невідомим коефіцієнтам мають вигляд
. Умови мінімізації функції (6.6) двох змінних за рівністю нулю частинних похідних по невідомим коефіцієнтам мають вигляд
 ;
;  .
.
Тоді маємо наступну систему рівнянь для визначення  та
та  :
:
(6.7)
або
(6.8)
Розв’язавши цю систему із двох лінійних рівнянь з двома невідомими, можна визначити невідомі коефіцієнти у рівнянні регресії за формулами
 ; (6.9)
; (6.9)
 . (6.10)
. (6.10)
Поліноміальна залежність. Ця залежність представляється у вигляді полінома  -го степеня
-го степеня
 . (6.11)
. (6.11)




 . Сумарний дисгармонічний коефіцієнт (5.57)
. Сумарний дисгармонічний коефіцієнт (5.57)  . Аналогічні обчислення проводимо для решти пар факторів. Результати розрахунків наведені у табл. 5.24.
. Аналогічні обчислення проводимо для решти пар факторів. Результати розрахунків наведені у табл. 5.24.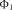 ) і всім комплексом. Маємо:
) і всім комплексом. Маємо:  ;
; .
. відкладають на кореляційному полі у відповідних інтервалах (позначені квадратами на рис. 6.1). Ламана лінія, яка з’єднує ці точки, називається
відкладають на кореляційному полі у відповідних інтервалах (позначені квадратами на рис. 6.1). Ламана лінія, яка з’єднує ці точки, називається