
При побудові лінійних моделей використовується метод включення змінних. Основним критерієм для визначення порядку включення факторів в модель є величина частинного коефіцієнту кореляції. Процедура побудови моделі включає такі операції.
1. Із скоригованої матриці парних коефіцієнтів кореляції вибирають перший фактор (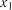 ), у якого коефіцієнт кореляції
), у якого коефіцієнт кореляції 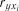 є найбіль-
є найбіль-
шим, і будують лінійне рівняння
 . (7.14)
. (7.14)
2. Для отриманого регресійного рівняння розраховують оціночні критерії якості: множинний коефіцієнт кореляції 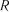 і множинний коефіцієнт детермінації
і множинний коефіцієнт детермінації 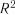 .
.
Множинний коефіцієнт кореляції характеризує силу зв’язку су-
купної комбінованої дії низки факторів на величину залежної змінної
 . Коефіцієнт множинної кореляції можна обчислити за такими формулами:
. Коефіцієнт множинної кореляції можна обчислити за такими формулами:
де 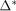 – визначник матриці парних коефіцієнтів кореляції;
– визначник матриці парних коефіцієнтів кореляції;
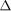 – визначник тієї ж самої матриці з викресленими першим рядком і першим стовпцем, тобто визначник матриці парних коефіцієнтів кореляції між факторами;
– визначник тієї ж самої матриці з викресленими першим рядком і першим стовпцем, тобто визначник матриці парних коефіцієнтів кореляції між факторами;
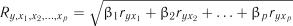 , (7.17)
, (7.17)
де  , ,
, , 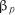 –стандартизовані коефіцієнти регресії (
–стандартизовані коефіцієнти регресії ( -коефіцієнти). Значення
-коефіцієнти). Значення  -коефіцієнтів обчислюють за формулою
-коефіцієнтів обчислюють за формулою
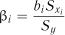 . (7.18)
. (7.18)

Квадрат множинного коефіцієнту кореляції  називається мно-
називається мно-
жинним коефіцієнтом детермінації і показує, яка частка диспер-
сії функції пояснюється за рахунок варіації лінійної комбінації вибраних факторів 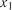 ,
, 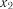 , ,
, ,  .
.
3. Із вектора частинних коефіцієнтів кореляції вибирають фактор
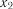 , який має найбільше значення частинного коефіцієнта кореля-
, який має найбільше значення частинного коефіцієнта кореля-
ції 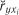 і знаходять друге рівняння регресії
і знаходять друге рівняння регресії
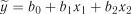 . (7.22)
. (7.22)
Якщо для двох або декількох факторів отримані однакові частинні коефіцієнти кореляції, то для визначення порядку включення факторів можна рекомендувати процедуру їх порівняння за критерієм
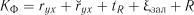 , (7.23)
, (7.23)
де 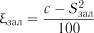 – коефіцієнт, який характеризує залишкову
– коефіцієнт, який характеризує залишкову
дисперсію; – будь-яке постійне число, що перевищує
значення залишкових дисперсій порівнюваних факторів.
В модель включається фактор з більшим значенням 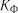 .
.
Пояснимо цю процедуру на прикладі. Нехай при розв’язанні задачі отримано такі статистики :
|
|
|
|
|
|
|
0,35 |
0,44 |
2,56 |
184 |
0,65 |
|
0,48 |
0,41 |
2,70 |
190 |
0,73 |
Для обчислення 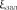 покладемо
покладемо 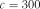 . Тоді маємо
. Тоді маємо
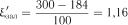 ;
; 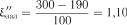 .
.
Обчислюємо величини: 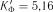 ;
; 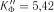 .
.
Отже, фактор  має перевагу перед фактором
має перевагу перед фактором  і включається в модель пер-
і включається в модель пер-
шочергово.
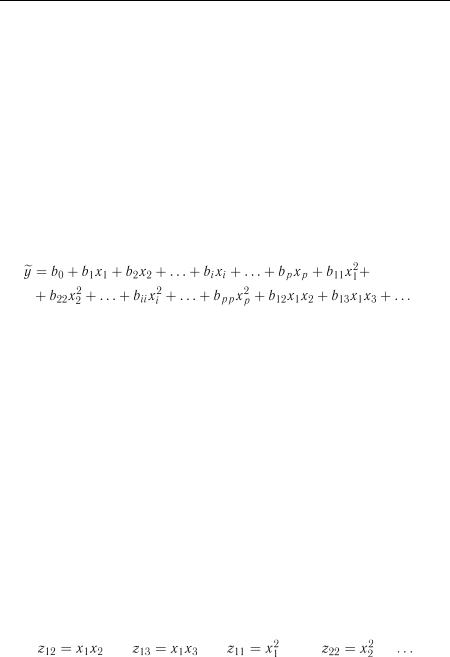
Апроксимація зв’язків багатофакторними регресійними моделями 331
4.Для отриманої в п. 3 моделі обчислюють 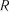 ,
, 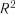 і
і 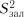 .
.
5.Включення факторів продовжується доти, доки 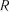 ,
, 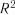 і
і 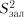 отриманих моделей покращуються, і може бути припинено, коли
отриманих моделей покращуються, і може бути припинено, коли
включення нового фактора викликає значне збільшення 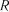 ,
, 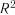 і
і
зменшення  .
.
6. Визначення адекватності регресійної залежності за 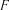 -критерієм Фішера. Виконується аналогічно однофакторним регресійним моделям
-критерієм Фішера. Виконується аналогічно однофакторним регресійним моделям
(див. розділ 6.2.4).
7.3.2. Нелінійні регресійні залежності.
Поліноміальна залежність. Функція представляється у вигляді полінома
(7.24)
Степінь рівняння можна підвищувати доти, доки зменшується залишкова дисперсія 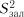 . Якщо не обмежувати степінь полінома і кількості членів, то можна апроксимувати будь-яку залежність з будьяким ступенем точності, однак на практиці, як правило, обмежують як степінь полінома так і кількість його членів. Практично для вироб- ничо-економічних задач достатньо задати поліном другого степеня.
. Якщо не обмежувати степінь полінома і кількості членів, то можна апроксимувати будь-яку залежність з будьяким ступенем точності, однак на практиці, як правило, обмежують як степінь полінома так і кількість його членів. Практично для вироб- ничо-економічних задач достатньо задати поліном другого степеня.
Для квадратичних форм і форм вищих порядків частинні коефіцієнти кореляції обчислити неможливо, для цих моделей застосовують два методи апроксимації:
1)метод виключення факторів (від складного до простого);
2)багатокроковий регресійний аналіз (змішаний метод).
7.3.2.1. Апроксимація методом виключення факторів. Алгоритм апроксимації включає такі процедури.
1.Побудова рівняння регресії у формі повної квадратичної і, за необхідності, повної кубічної залежності .
2.Заміна кожного складного члена полінома додатковою умовною змінною у першій степені:
Приведення полінома до лінійної форми
3.Складання системи нормальних рівнянь і ідентифікація параметрів регресійної моделі.
4.Перевірка коефіцієнтів регресії на значимість за  -критерієм
-критерієм
Стьюдента.
5.Виключення незначимих членів регресійного рівняння.
6.Обчислення множинного кореляційного відношення
. (7.25)
7. Перевірка значимості кореляційного відношення за допомогою 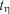 -критерію, який характеризується розподілом Стьюдента з
-критерію, який характеризується розподілом Стьюдента з
 ступенями вільності
ступенями вільності
де  – стандартна похибка множинного кореляційного відношення. Величина
– стандартна похибка множинного кореляційного відношення. Величина  визначається за формулою
визначається за формулою
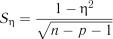 . (7.27)
. (7.27)
9.Розрахунок залишкової дисперсії  і
і 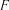 -критерію Фішера.
-критерію Фішера.
10.Перевірка адекватності моделі 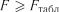 для прийнятого рівня значимості
для прийнятого рівня значимості  .
.
11.Викреслювання із матриці нормальних рівнянь відповідних рядків і стовпців.
Апроксимація зв’язків багатофакторними регресійними моделями 333
12. Визначення для отриманої матриці коефіцієнтів регресії, перевірка їх на значимість, виключення незначимих із розгляду і т. д. доти, доки не буде отримано вираз, всі коефіцієнти якого будуть значимими і модель регресії буде адекватною за  -критерієм.
-критерієм.
7.3.2.2. Багатокроковий регресійний аналіз. Задача полягає у тому, щоб встановити, на якому члені рівняння можна припинити (перервати) ряд, щоб отриманий відрізок був значимим з заданою імовірністю.
Процес пошуку значимого відрізка рівняння здійснюється таким чином. Спочатку в модель включаються всі невідомі у перших степенях
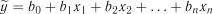 .
.
Якщо після оцінки за  -критерієм цей вираз буде незначимим, то його слід подовжити, додаючи значення невідомих з парними добутками, в квадраті і т.д. Процес підвищування степеня полінома продовжується до тих пір, доки відрізок рівняння не стане значимим.
-критерієм цей вираз буде незначимим, то його слід подовжити, додаючи значення невідомих з парними добутками, в квадраті і т.д. Процес підвищування степеня полінома продовжується до тих пір, доки відрізок рівняння не стане значимим.
При багатокроковому регресійному аналізі з метою виявлення значимих членів рівняння відсіюють несуттєві члени. Для цього здійснюють оцінку значимості коефіцієнтів регресії за допомогою критерію 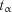 Стьюдента. Член рівняння, для якого значення
Стьюдента. Член рівняння, для якого значення 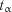 є найменшим, вважають незначимим і виключають із рівняння. Після цього визначають параметри рівняння регресії для (
є найменшим, вважають незначимим і виключають із рівняння. Після цього визначають параметри рівняння регресії для ( ) членів і вся процедура починається спочатку. Процес виключення не значимих членів рівняння продовжують до тих пір, доки всі коефіцієнти регресії у рівнянні не стануть значимими, а сама модель – адекватною.
) членів і вся процедура починається спочатку. Процес виключення не значимих членів рівняння продовжують до тих пір, доки всі коефіцієнти регресії у рівнянні не стануть значимими, а сама модель – адекватною.
Блок-схема цього алгоритму представлена на рис. 7.1.
Степенева залежність має вигляд
. (7.28)
Для знаходження параметрів моделі її слід лініювати, взявши логарифм від правої та лівої частини рівняння
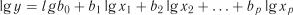 . (7.29)
. (7.29)
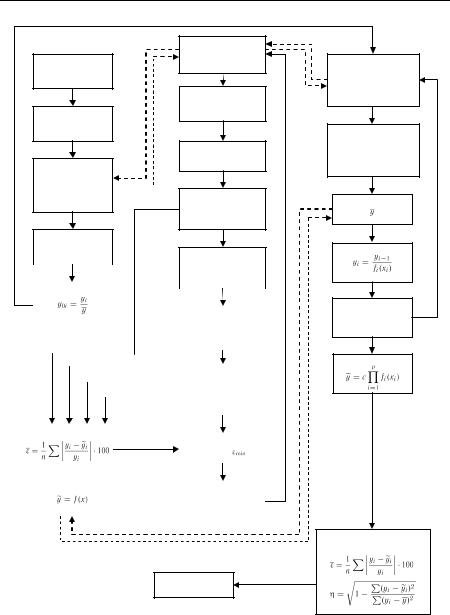
1.Введення вихідних даних x, y
2.Обчислення середнього значення 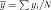
3. Обчислення дисперсії
4. Формування системи нормальних рівнянь
5.Розрахунок елементів оберненої матриці 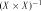
6.Обчислення коефіцієнтів регресії 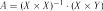
7. Обчислення розрахункових значень незалежної змінної
8.Обчислення залишкової дисперсії 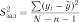
9.Перевірка на зменшення 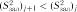 , де j - номер кроку
, де j - номер кроку
10.Обчислення F-критерію 
11.Перевірка адекватності 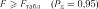
 ні
ні
12.Розширення матриці Х для здобуття полінома 2-го ступеня
13.Обчислення багатофакторного кореляційного відношення
14.Обчислення стандартної похибки коефіцієнтів регресії 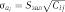
15. Обчислення t-критерію для коефіцієнтів регресії
так
16. Оцінка членів рівняння регресії за t-критерієм 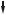 ні
ні
17.Виключення відповідного рядка та стовпчика матриці Х
18.Фіксування результатів розрахунку
Рис. 7.1. Блок-схема алгоритму багатокрокового регресійного аналізу
Апроксимація зв’язків багатофакторними регресійними моделями 335
Зробимо заміну змінних:  ;
; 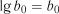 ;
; 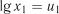 ;
; 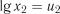 ; ;
; ; 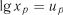 . Тоді залежність набуде вигляду
. Тоді залежність набуде вигляду
. (7.30)
Параметри моделі відшукуються методом найменших квадратів. Після того як будуть знайдені всі параметри моделі, можна перейти до шуканої моделі шляхом потенціювання.
Показникова залежність має вигляд
. (7.31)
Для апроксимації рівняння його слід лініювати шляхом логарифмування і після цього методом найменших квадратів знайти невідомі коефіцієнти.
Залежність у вигляді добутку ряду функцій (метод Брандо-
на) має вигляд
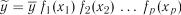 . (7.32)
. (7.32)
Залежності 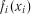 можуть бути різними функціями: лінійною, параболічною, степеневою тощо. Розв’язання задачі полягає у визначенні величини
можуть бути різними функціями: лінійною, параболічною, степеневою тощо. Розв’язання задачі полягає у визначенні величини 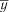 і виразу функцій
і виразу функцій 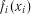 в такій послідовності.
в такій послідовності.
1. Розраховується середнє значення 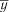 , після чого фактичні значен-
, після чого фактичні значен-
ня y замінюються нормалізованими
 . (7.33)
. (7.33)
2. Вибирається вид взаємозв’язку 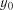 від
від 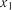 і методом найменших квадратів визначаються параметри залежності
і методом найменших квадратів визначаються параметри залежності
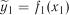 . (7.34)
. (7.34)
3. За отриманою емпіричною залежністю розраховується значення функції 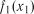 і визначається залишковий показник
і визначається залишковий показник  для кожного спостереження
для кожного спостереження
|
. |
|
(7.35) |
Цей залишковий результат уже не буде залежати від |
, а зале- |
жить тільки від , , , |
|
|
|
|
. |
(7.36) |
4. |
Визначається регресійна модель залежності |
від |
|
|
. |
|
(7.37) |
5. |
Знову визначається умовний показник |
|
|
|
|
|
. (7.38) |
6. Такий розрахунок здійснюється до тих пір, доки не будуть визначені всі функції 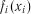 . Останнім розраховується умовний показник
. Останнім розраховується умовний показник
|
. |
(7.39) |
Після цього відшукується аналітичне значення |
. |
|
Таким чином, після того як будуть розраховані значення всіх |
, |
модель представляється як добуток всіх відшуканих функцій |
|
|
. |
(7.40) |
На рис 7.2 представлена блок-схема апроксимації регресійної залежності (7.32). Апроксимація парних залежностей здійснюється такими функціями:
– лінійною |
; |
– параболічною |
; |
– степеневою |
; |
– тригонометричною 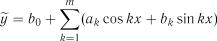 ,
,
де k 1, 2, ..., m є задана кількість гармонік.
Апроксимація зв’язків багатофакторними регресійними моделями 337
14. Початок
внутрішнього циклу
1. Введення вихідних даних
15. Виклик  в
в
робочий масив
2. Занесення 
в робочий масив
16. Нульовий цикл
3. Розрахунок парних регресійних 
залежностей 17. Апроксимація парної залежності
прямою лінією
4.Аналіз факторів на значущість
|
|
|
|
|
|
|
|
|
|
|
|
18. Апроксимація |
|
|
|
|
|
|
|
|
|
|
|
|
парної залежності |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параболою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Нормалізація |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. Апроксимація |
|
|
|
|
|
|
|
|
|
|
|
|
парної залежності |
|
|
|
|
|
|
|
|
|
|
|
|
степеневою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функцією |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. Апроксимація |
|
|
|
|
|
|
|
|
|
|
|
|
парної залежності |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тригонометричною |
|
|
|
|
|
|
|
|
|
|
|
|
функцією |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21.Обчислення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22. Вибір мінімальної |
|
|
|
|
|
|
|
|
|
|
|
|
похибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24.Обчислення: |
|
|
|
|
|
23. Засилання |
|
|
|
|
|
|
|
|
|
|
|
|
мінімальних |
|
|
|
|
|
|
|
|
|
|
|
|
параметрів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. Кінець
6. Розрахунок додаткових парних регресійних залежностей
7. Аналіз отриманих залежностей на відповідність причинним зв’язкам
8.Обчислення
9.Перетворення
10.Порівняння ні
 ?
?
11.Обчислення
12. Обчислення
 ;
;
;
Рис. 7.2. Блок-схема апроксимації регресійної залежності методом Брандона



 , то всі точки кореляційного простору розташовані на поверхні регресії, тобто маємо функціональний зв’язок. Якщо
, то всі точки кореляційного простору розташовані на поверхні регресії, тобто маємо функціональний зв’язок. Якщо  , то кореляційний зв’язок між функцією і аргументом відсутній.
, то кореляційний зв’язок між функцією і аргументом відсутній. -критерієм Стьюдента. Для цього розраховується величина
-критерієм Стьюдента. Для цього розраховується величина – стандартна похибка коефіцієнта множинної
– стандартна похибка коефіцієнта множинної порівнюється з табличним
порівнюється з табличним 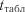 для вибраного рівня значимості
для вибраного рівня значимості  і кількістю ступенів вільності
і кількістю ступенів вільності  . Якщо
. Якщо  , то коефіцієнт множинної кореляції вважається значимим.
, то коефіцієнт множинної кореляції вважається значимим.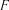 -критерієм Фішера з використанням формули
-критерієм Фішера з використанням формули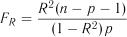 . (7.20)
. (7.20)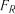 порівнюють з табличним, яке визначається за таблицею розподілу Фішера для прийнятого рівня значимості
порівнюють з табличним, яке визначається за таблицею розподілу Фішера для прийнятого рівня значимості  і кількості ступенів вільності
і кількості ступенів вільності  та
та 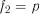 . Якщо
. Якщо 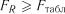 , то коефіцієнт кореляції
, то коефіцієнт кореляції 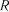 вважається значимим.
вважається значимим.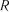 повинна бути скоригованою за формулою
повинна бути скоригованою за формулою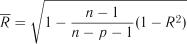 . (7.21)
. (7.21)
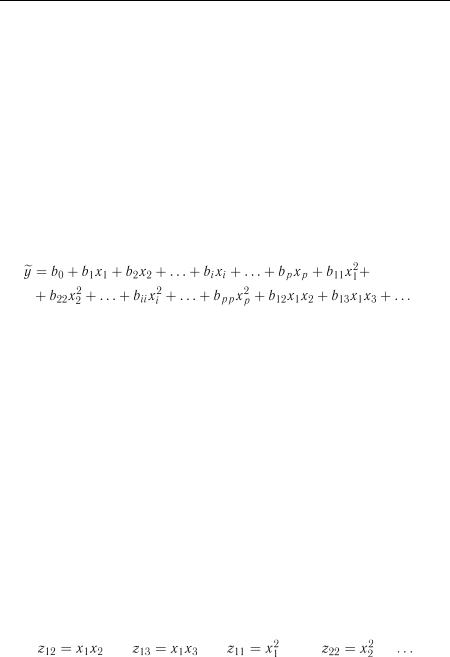


 -критерієм.
-критерієм.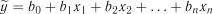 .
. -критерієм цей вираз буде незначимим, то його слід подовжити, додаючи значення невідомих з парними добутками, в квадраті і т.д. Процес підвищування степеня полінома продовжується до тих пір, доки відрізок рівняння не стане значимим.
-критерієм цей вираз буде незначимим, то його слід подовжити, додаючи значення невідомих з парними добутками, в квадраті і т.д. Процес підвищування степеня полінома продовжується до тих пір, доки відрізок рівняння не стане значимим.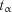 Стьюдента. Член рівняння, для якого значення
Стьюдента. Член рівняння, для якого значення 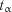 є найменшим, вважають незначимим і виключають із рівняння. Після цього визначають параметри рівняння регресії для (
є найменшим, вважають незначимим і виключають із рівняння. Після цього визначають параметри рівняння регресії для ( ) членів і вся процедура починається спочатку. Процес виключення не значимих членів рівняння продовжують до тих пір, доки всі коефіцієнти регресії у рівнянні не стануть значимими, а сама модель – адекватною.
) членів і вся процедура починається спочатку. Процес виключення не значимих членів рівняння продовжують до тих пір, доки всі коефіцієнти регресії у рівнянні не стануть значимими, а сама модель – адекватною.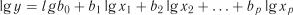 . (7.29)
. (7.29)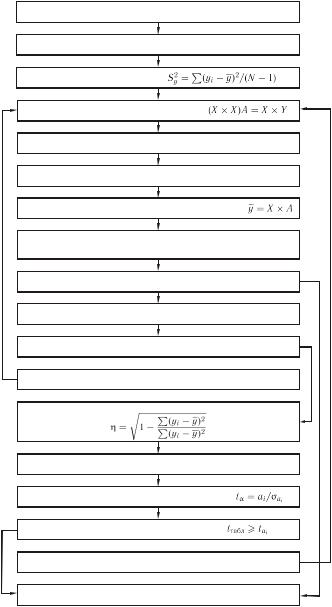

 ;
; 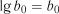 ;
; 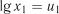 ;
; 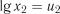 ; ;
; ; 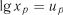 . Тоді залежність набуде вигляду
. Тоді залежність набуде вигляду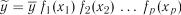 . (7.32)
. (7.32)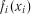 можуть бути різними функціями: лінійною, параболічною, степеневою тощо. Розв’язання задачі полягає у визначенні величини
можуть бути різними функціями: лінійною, параболічною, степеневою тощо. Розв’язання задачі полягає у визначенні величини 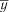 і виразу функцій
і виразу функцій 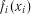 в такій послідовності.
в такій послідовності.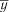 , після чого фактичні значен-
, після чого фактичні значен- . (7.33)
. (7.33)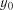 від
від 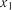 і методом найменших квадратів визначаються параметри залежності
і методом найменших квадратів визначаються параметри залежності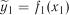 . (7.34)
. (7.34)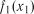 і визначається залишковий показник
і визначається залишковий показник  для кожного спостереження
для кожного спостереження

 ), у якого коефіцієнт кореляції
), у якого коефіцієнт кореляції  є
є  . (7.14)
. (7.14) і
і 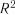 .
. . Коефіцієнт множинної кореляції можна обчислити за такими формулами:
. Коефіцієнт множинної кореляції можна обчислити за такими формулами: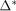 – визначник матриці парних коефіцієнтів кореляції;
– визначник матриці парних коефіцієнтів кореляції;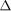 – визначник тієї ж самої матриці з викресленими
– визначник тієї ж самої матриці з викресленими 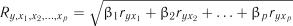 , (7.17)
, (7.17) , ,
, , 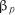 –стандартизовані коефіцієнти регресії (
–стандартизовані коефіцієнти регресії ( -коефіцієнти). Значення
-коефіцієнти). Значення  -коефіцієнтів обчислюють за формулою
-коефіцієнтів обчислюють за формулою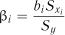 . (7.18)
. (7.18) називається
називається 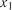 ,
, 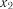 , ,
, ,  .
.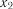
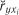 і знаходять друге рівняння регресії
і знаходять друге рівняння регресії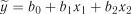 . (7.22)
. (7.22)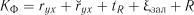 , (7.23)
, (7.23)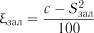 – коефіцієнт, який характеризує залишкову
– коефіцієнт, який характеризує залишкову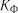 .
.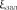 покладемо
покладемо 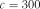 . Тоді маємо
. Тоді маємо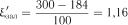 ;
; 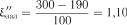 .
.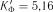 ;
; 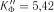 .
. має перевагу перед фактором
має перевагу перед фактором  і включається в модель
і включається в модель 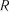 ,
, 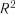 і
і 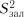 .
.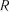 ,
, 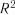 і
і 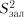 отриманих моделей покращуються, і
отриманих моделей покращуються, і 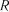
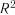

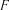 -критерієм Фішера. Виконується аналогічно однофакторним регресійним моделям
-критерієм Фішера. Виконується аналогічно однофакторним регресійним моделям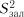 . Якщо не обмежувати степінь полінома і кількості членів, то можна апроксимувати будь-яку залежність з будьяким ступенем точності, однак на практиці, як правило, обмежують
. Якщо не обмежувати степінь полінома і кількості членів, то можна апроксимувати будь-яку залежність з будьяким ступенем точності, однак на практиці, як правило, обмежують  -критерієм
-критерієм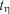 -критерію, який характеризується розподілом Стьюдента з
-критерію, який характеризується розподілом Стьюдента з ступенями вільності
ступенями вільності – стандартна похибка множинного кореляційного відношення. Величина
– стандартна похибка множинного кореляційного відношення. Величина  визначається за формулою
визначається за формулою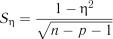 . (7.27)
. (7.27) і
і 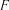 -критерію Фішера.
-критерію Фішера.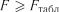 для прийнятого рівня значимості
для прийнятого рівня значимості  .
.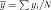
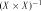
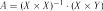
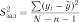
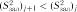 , де
, де 
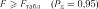
 ні
ні
 ні
ні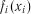 . Останнім розраховується умовний показник
. Останнім розраховується умовний показник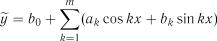 ,
, в
в

 ?
? ;
;