big_doc_LKG
.pdf
120 |
Розділ 2 |
|
Розрахунок критерію |
для експоненціального розподілу |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Щільність розподілу |
|
h |
|
|
|||
|
|
|
|
|
|
|
|
|
|
i |
|
|
Інтервал t |
Середина інтервалу |
|
|
|
|
|
|
|
P 10 |
P 10 |
|
|
|
|
|
|
|
емпірична |
теоретична |
ц |
ц)] |
|
|
||
|
|
|
|
|
|
|
|
|
) |
2 |
|
|
ц |
|
mi |
hi |
|
|
|
|
|
–f(t –3 |
f(t –3 |
|
|
|
|
|
|
|
, |
|
||||||
|
|
|
|
, |
|
|
– |
|
|
|||
|
|
|
|
|
|
|
* і |
|
|
|||
|
|
|
|
|
|
|
10 |
–3 |
|
* |
|
|
|
|
|
|
|
|
10–3 |
|
[ |
|
|
||
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20–40 |
30 |
30 |
20 |
0,30 |
|
15 |
9,87 |
5,13 |
0,526 |
|
0,053 |
|
40–60 |
50 |
22 |
20 |
0,22 |
|
11 |
7,17 |
3,83 |
0,292 |
|
0,041 |
|
60–80 |
70 |
16 |
20 |
0,16 |
|
8 |
5,2 |
2,8 |
0,156 |
|
0,030 |
|
80–100 |
90 |
20 |
20 |
0,20 |
|
10 |
3,82 |
0,618 |
0,762 |
|
0,020 |
|
100–120 |
110 |
8 |
40 |
0,08 |
|
3 |
2,36 |
0,64 |
0,016 |
|
0,007 |
|
120–140 |
130 |
|
0,04 |
|
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
100 |
|
|
|
|
|
|
|
|
|
|
Приклад 3. Розглянемо випадкову величину – тривалість простою одного вагона під навантаженням металопрокатом на складі готової продукції металургійного комбінату. Згруповані дані наведені в наступній таблиці.
Тривалість |
0–46 |
46–92 |
92–138 |
138–184 |
184–230 |
230–276 |
276–322 |
322–368 |
368–414 |
|
простою вагона |
||||||||||
, хв. |
|
|||||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Частота, |
4 |
48 |
35 |
30 |
14 |
12 |
2 |
3 |
2 |
150 |
Необхідно апроксимувати дані теоретичним законом розподілу.
Розв’язок.
1. За даними вихідної таблиці частот будуємо гістограму і емпіричну функцію розподілу тривалості навантаження у вигляді полігону розподілу. За зовнішньою формою полігону робимо припущення, що для апроксимації випадкової величини можна застосувати один з таких теоретичних законів розподілу: Ерланга, гамма-розподіл, Вей-
булла, Релея.
Розрахункові статистичні характеристики випадкової величини мають такі значен-
ня: 
хв., 
хв.
Апроксимація законом Ерланга. Функція щільності імовірності закону розподілу Ерланга (табл. 2.4) має вигляд
Ідентифікація параметрів статистичними законами розподілу |
121 |
. |
|
m |
|
t, . |
|
Обчислюємо оцінки параметрів закону |
|
; |
. |
Тоді маємо
.
Всі подальші розрахунки наведені у розрахунковій таблиці. Обчислюємо міру розбіжності
.
Закон розподілу Ерланга є двохпараметричним. Кількість інтервалів 
, кількість ступенів вільності 
. У додатку Д3 знаходимо критичне значення 
.
.
122 |
Розділ 2 |
Отже, нульова гіпотеза щодо узгодження емпіричного розподілу теоретичному закону Ерланга не підтверджується.
Процедура апроксимації емпіричного розподілу законом Ерланга
хв, . |
хв. |
|
, |
|
|
|
|
|
, |
|
|
|
|
|
|
||
i |
Частотат |
i |
10–3 |
|
–3 |
|
||
Інтервалчасу, t |
Серединаінтервалуt |
Емпіричначастість |
f |
|
p |
|
||
i |
|
і |
|
m |
Щільність розподілу |
10 |
|
|
|
|
|
|
/ |
|
|
), |
|
|
|
|
|
i |
|
|
t ( |
|
|
|
|
|
т= |
|
|
T |
|
|
|
|
|
|
|
–f |
|
|
|
|
|
|
емпірична |
теоретична |
|
||
|
|
|
|
Е |
* |
|
||
|
|
|
|
|
|
, |
N |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
10–3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0–46 |
23 |
4 |
0,027 |
0,59 |
4,13 |
–3,54 |
0,139 |
|
46–92 |
69 |
48 |
0,320 |
6,96 |
5,91 |
1,05 |
0,008 |
|
92–138 |
115 |
35 |
0,233 |
5,06 |
4,70 |
0,36 |
0,001 |
|
138–184 |
161 |
30 |
0,200 |
4,35 |
3,14 |
1,21 |
0,021 |
|
184–230 |
207 |
14 |
0,093 |
2,02 |
1,93 |
0,09 |
0,000 |
|
230–276 |
253 |
12 |
0,080 |
1,73 |
1,12 |
0,61 |
0,015 |
|
276–322 |
299 |
2 |
0,013 |
0,28 |
0,63 |
–0,35 |
0,009 |
|
322–368 |
345 |
3 |
0,020 |
0,43 |
0,57 |
–0,14 |
0,001 |
|
368–414 |
391 |
2 |
0,013 |
0,28 |
0,19 |
0,09 |
0,001 |
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
Апроксимація гамма-розподілом. Щільність гамма-розподілу описується залежністю (табл. 2.4)
.
Знаходимо оцінки параметрів закону за формулами табл. 2.4:
|
; |
. |
Значення гамма-функції |
наведені у табл. 2.5, звідки маємо |
. |
Ідентифікація параметрів статистичними законами розподілу |
123 |
Після підстановки в формулу для 
значень параметрів і здійснення відповідних перетворень, отримаємо залежність для приблизної оцінки теоретичного розподілу тривалості простою вагонів
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
Таблиця 2.5 |
|
|
Таблиця значень гамма-функції |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
9,5135 |
|
1,5 |
0,8862 |
3 |
|
2,0000 |
0,2 |
4,5908 |
|
1,6 |
0,8935 |
3,1 |
|
2,1976 |
0,3 |
2,9916 |
|
1,7 |
0,9086 |
3,2 |
|
2,4240 |
0,4 |
2,2182 |
|
1,8 |
0,9314 |
3,3 |
|
2,6834 |
0,5 |
1,7725 |
|
1,9 |
0,9618 |
3,4 |
|
2,9812 |
0,6 |
1,4892 |
|
2 |
1,0000 |
3,5 |
|
3,3234 |
0,7 |
1,2981 |
|
2,1 |
1,0465 |
3,6 |
|
3,7170 |
0,8 |
1,1642 |
|
2,2 |
1,1018 |
3,7 |
|
4,1707 |
0,9 |
1,0686 |
|
2,3 |
1,1667 |
3,8 |
|
4,6942 |
1,0 |
1,0000 |
|
2,4 |
1,2422 |
3,9 |
|
5,2993 |
1,1 |
0,9514 |
|
2,5 |
1,3293 |
4 |
|
6,0000 |
1,2 |
0,9182 |
|
2,6 |
1,4296 |
4,1 |
|
6,8126 |
1,3 |
0,8975 |
|
2,7 |
1,5447 |
4,2 |
|
7,7567 |
1,4 |
0,8873 |
|
2,8 |
1,6765 |
4,3 |
|
8,8553 |
1,5 |
0,8862 |
|
2,9 |
1,8274 |
4,4 |
|
10,1361 |
Результати розрахунків наведені в таблиці.
Процедура апроксимації емпіричного розподілу гамма-розподілом
хв. |
хв. |
|
, |
i |
|
||
Інтервалчасу, t |
, |
Частотат |
Емпіричначастість f |
Серединаінтервалу t |
|||
, |
|
і |
i |
i |
|
|
m |
|
|
|
/ |
|
|
|
i |
|
|
|
т= |
|
|
|
Е |
|
|
|
|
0–46 |
23 |
4 |
0,027 |
46–92 |
69 |
48 |
0,320 |
92–138 |
115 |
35 |
0,233 |
138–184 |
161 |
30 |
0,200 |
|
|
|
|
Щільність розподілу
емпірична |
теоретична |
|
, |
, |
|
10–3 |
||
10–3 |
||
|
||
0,59 |
2,77 |
|
6,96 |
6,30 |
|
5,06 |
5,54 |
|
4,35 |
3,56 |
|
|
|
p * – f (t), 10–3 N T
–2,18 0,078 0,86 0,003 –0,48 0,002 0,79 0,008
124 |
Розділ 2 |
184–230 |
207 |
14 |
0,093 |
|
2,02 |
2,02 |
0,0 |
0,000 |
230–276 |
253 |
12 |
0,080 |
|
1,73 |
1,06 |
0,67 |
0,020 |
276–322 |
299 |
2 |
0,013 |
|
0,28 |
0,53 |
–0,25 |
0,005 |
322–368 |
345 |
3 |
0,020 |
|
0,43 |
0,25 |
0,18 |
0,006 |
368–414 |
391 |
2 |
0,013 |
|
0,28 |
0,12 |
0,16 |
0,010 |
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
Обчислюємо міру розбіжності |
|
|
|
|
||||
|
|
|
|
|
|
|
. |
|
Так як розрахункове значення 
перевищує табличне значення критерію 
, то гіпотетично прийнятий гамма-розподіл не може бути застосований для математичного опису тривалості простою вагонів.
Перевірку узгодженості емпіричного розподілу теоретичним законам Вейбулла і Релея виконано за формулою (2.8) з використанням інтегральних функцій розподілу випадкової величини 
.
Процедура апроксимації емпіричного розподілу розподілом Вейбулла
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0–46 |
23 |
4 |
1,0 |
0,8521 |
0,1479 |
22,18 |
330,51 |
14,9 |
46–92 |
69 |
48 |
0,8521 |
0,6052 |
0,2469 |
37,04 |
120,12 |
3,24 |
92–138 |
115 |
35 |
0,6052 |
0,3753 |
0,2299 |
34,48 |
0,27 |
0,01 |
138–184 |
161 |
30 |
0,3753 |
0,2039 |
0,1714 |
25,71 |
18,40 |
0,72 |
184–230 |
207 |
14 |
0,2039 |
0,1003 |
0,8997 |
15,54 |
2,37 |
0,15 |
230–276 |
253 |
12 |
0,1003 |
0,0446 |
0,0557 |
8,36 |
13,25 |
1,58 |
276–322 |
299 |
2 |
0,0446 |
0,0185 |
0,0261 |
3,92 |
3,69 |
0,94 |
322–368 |
345 |
3 |
0,0185 |
0,0069 |
0,0116 |
1,74 |
1,59 |
0,91 |
368–414 |
391 |
2 |
0,0069 |
0,0025 |
0,0044 |
0,66 |
1,80 |
2,72 |
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
149,63 |
|
25,17 |
Ідентифікація параметрів статистичними законами розподілу |
125 |
.
.
.
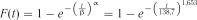Процедура апроксимації емпіричного розподілу розподілом Релея
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0–46 |
23 |
4 |
1,0000 |
0,9324 |
0,0676 |
10,14 |
37,70 |
3,72 |
46–92 |
69 |
48 |
0,9324 |
0,7334 |
0,1990 |
29,85 |
329,42 |
11,03 |
92–138 |
115 |
35 |
0,7334 |
0,4960 |
0,2374 |
35,61 |
0,37 |
0,01 |
138–184 |
161 |
30 |
0,4960 |
0,2894 |
0,2066 |
30,99 |
0,98 |
0,03 |
184–230 |
207 |
14 |
0,2894 |
0,1437 |
0,1457 |
21,85 |
61,62 |
2,82 |
230–276 |
253 |
12 |
0,1437 |
0,0614 |
0,0823 |
12,34 |
0,12 |
0,01 |
276–322 |
299 |
2 |
0,0614 |
0,0226 |
0,0388 |
5,82 |
14,59 |
2,51 |
322–368 |
345 |
3 |
0,0226 |
0,0070 |
0,0156 |
2,34 |
0,44 |
0,19 |
368–414 |
391 |
2 |
0,0070 |
0,0019 |
0,0051 |
0,77 |
1,51 |
1,86 |
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
149,7 |
|
22,28 |
;
;
.
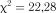Аналіз результатів перевірки показує, що законами розподілу Вейбулла та Релея також не можна апроксимувати розглядуваний вхідний параметр.
Приклад 4. Дані про кількість автомобілів, які прибувають на станцію технічного обслуговування (СТО) протягом інтервалу часу t = 1,0 год., представлені статистичним рядом розподілу.
Кількість |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
автомобілів |
||||||||
|
|
|
|
|
|
|
||
Частота |
18 |
35 |
25 |
10 |
7 |
5 |
100 |
126 |
Розділ 2 |
Обґрунтувати теоретичний закон інтенсивності прибуття автомобілів на станцію технічного обслуговування, на основі якого можна побудувати математичну модель вхідного потоку автомобілів.
Розв’язок.
1. Досліджуваний параметр являє собою дискретну випадкову величину, розподіл якої графічно можна представити полігоном частот:
mi
k
2.Вид теоретичного закону вибираємо згідно з табл. 2.3 для розподілу дискретних випадкових величин. Візуальний аналіз полігону показує, що для апроксимації даного емпіричного ряду гіпотетично можна прийняти закон розподілу Пуассона.
3.Визначаємо параметр закону розподілу 
. Параметр 
характеризує інтенсив-
ність вхідного потоку (середню кількість автомобілів, що надходять за прийнятий інтервал часу) і дорівнює
.
Тоді для даних умов закон Пуассона можна записати у вигляді
.
4. Розраховуємо імовірності 
та за формулою (2.5) критерій 
. Результати розрахунків наведені в таблиці.
Кількість |
Частота |
Теоретична |
|
|
|
автомобілів |
|
імовірність |
|
|
|
|
|
|
|
|
|
|
Ідентифікація параметрів статистичними законами розподілу |
127 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
18 |
0,1864 |
|
18,64 |
0,4096 |
|
0,022 |
|
|
1 |
|
35 |
0,3132 |
|
31,32 |
13,54 |
|
0,4324 |
|
|
|
2 |
|
25 |
0,2630 |
|
26,30 |
1,63 |
|
0,0642 |
|
|
|
3 |
|
10 |
0,1473 |
|
14,73 |
22,37 |
|
1,5188 |
|
|
|
4 |
|
7 |
0,0619 |
|
6,19 |
0,6561 |
|
0,1060 |
|
|
|
5 |
|
5 |
0,0208 |
|
2,08 |
8,5264 |
|
4,099 |
|
|
|
|
|
100 |
|
100 |
|
|
6,243 |
|
|
||
|
5. Закон розподілу Пуассона є однопараметричним. У додатку Д3 |
для кількості |
|||||||||
ступенів |
вільності |
і |
рівня значимості |
знаходимо |
|||||||
. Так як 
менше ніж 
, то гіпотеза щодо розподілу автомобільного потоку, що прибуває на СТО, за законом Пуассона підтверджу-
ється.
2.4.1.2. Критерії, засновані на порівнянні теоретичної і емпіричної функції розподілу імовірностей. Різниця між емпіричною 
і теоретичною 
функціями розподілу ймовірностей є доволі ефективною статистикою для перевірки гіпотез про вид закону розподілу ймовірностей випадкової величини. Емпіричну функцію розподілу випадкової величини 
можна представити у вигляді
(2.12)
Якщо функція теоретичного розподілу вірогідно невідома і тільки промовляється гіпотеза, згідно з якою ця функція, є деякою заданою функцією неперервного розподілу 
з відомими параметрами, то, позначивши таку гіпотезу символом 
, можемо умовно записати її у вигляді тотожності
, 
.
Так само можна виразити нерівностями конкуруючі з 
гіпотези:
; 
; (2.13)
128 |
Розділ 2 |
.
Тут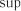 
, 
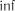– точні верхня і нижня межі відповідних різностей. Серед відомих критеріїв згоди такого типу відзначимо серію крите-
ріїв, що використовують різні варіанти аналізу різниці між значеннями
і 
.
При розгляданні критеріїв цієї групи припускається знання теоретичного закону з точністю до параметрів. У випадку відсутності надійної інформації про параметри розподілу слід користуватися спеціаль-
ними критеріями нормальності і експоненціальності розподілів.
Критерії Колмогорова-Смірнова. Ці критерії призначені для перевірки гіпотези 
по відношенню до конкуруючих гіпотез 
, 
та 
, підраховування критерію здійснюється за негрупованими ви-
бірками великого обсягу (
). Для деяких модифікацій критерію можна використати і груповані дані, але при цьому потужність критерію знижується на 5–15%.
Статистики критеріїв задаються формулами:
;
; (2.14)
,
де в лівих частинах тотожностей знаки + та –, а також відсутність знаку вказує відповідну конкуруючу гіпотезу.
Для практичних обчислень цих статистик використовують такі залежності:
;
; (2.15)
Ідентифікація параметрів статистичними законами розподілу |
129 |
|
|
|
. |
|
|
Якщо гіпотеза |
є вірною, то статистики |
і |
мають одна- |
||
ковий розподіл. За умов |
або |
|
гіпотеза |
||
відхиляється. |
|
|
|
|
|
При |
критичне значення |
на відрізку |
|
||
та 
при 
можна приблизно розрахувати за такою формулою
, (2.16)
де 
, якщо обчислюється 
і 
, як-
що обчислюється 
. У додатку Д7 наведені критичні значення критерію для найбільшого відхилення.
В дослідницькій практиці використовуються також перетворені
статистики: |
|
– верхня точка; |
|
– нижня точка; |
(2.17) |
. |
|
В цих виразах критичні значення статистики не залежать від 
і на рівні значимості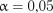 
дорівнюють
Приклад 5. Перевірити нормальність розподілу статистичних даних прикладу 1 на рівні значимості 
.