big_doc_LKG
.pdf
140 |
Розділ 2 |
Якщо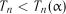 
, то гіпотеза експоненціальності розподілу відхиляється. Критичні значення 
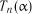наведені у табл. 2.10.
|
|
|
|
|
|
|
|
|
|
Таблиця 2.10 |
|
|
Критичні значення |
|
|
для |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2,2265 |
|
7 |
2,5046 |
|
12 |
2,4724 |
|
17 |
2,4235 |
|
3 |
2,3923 |
8 |
2,5029 |
13 |
2,4627 |
18 |
2,4141 |
|
|||
4 |
2,4536 |
9 |
2,4976 |
14 |
2,4528 |
19 |
2,4049 |
|
|||
5 |
2,4863 |
10 |
2,4903 |
15 |
2,4429 |
20 |
2,3559 |
|
|||
6 |
2,5006 |
11 |
2,4817 |
16 |
2,4335 |
|
|
|
|
||
Приклад 10. За даними прикладу 8 перевірити експоненціальність розподілу інтервалів прибуття автомобілів за критерієм Кочара на рівні значимості 
.
Розв’язок. Маємо:
;
;
; 
; 
;
; 
; 
;
; 
;
.
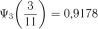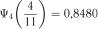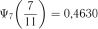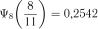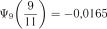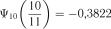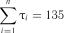Отримуємо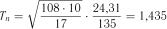 
.
Ідентифікація параметрів статистичними законами розподілу |
141 |
Із табл. 2.10 для 
знаходимо критичне значення 
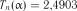. Так як 
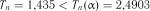, то гіпотеза експоненціальності розподілу досліджуваної величини підтверджується.
Критерій Шермана. Статистика критерію має вигляд
. (2.37)
Критичні значення 
на рівні значимості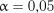 
наведені в табл. 2.11.
|
|
|
|
|
|
Таблиця 2.11 |
|
|
Критичні значення |
для |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0,475 |
8 |
0,482 |
|
15 |
0,458 |
2 |
|
0,537 |
9 |
0,477 |
|
16 |
0,455 |
3 |
|
0,518 |
10 |
0,473 |
|
17 |
0,453 |
4 |
|
0,509 |
11 |
0,469 |
|
18 |
0,451 |
5 |
|
0,502 |
12 |
0,466 |
|
19 |
0,449 |
6 |
|
0,494 |
13 |
0,463 |
|
20 |
0,448 |
7 |
|
0,488 |
14 |
0,460 |
|
|
|
|
|
|
|
|
|
|
|
При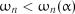 
нульова гіпотеза 
підтверджується.
Приклад 11. Для даних прикладу 8 перевірити гіпотезу експоненціальності розподілу інтервалів прибуття автомобілів за критерієм Шермана на рівні значимості
.
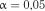Розв’язок. Маємо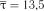 
. За формулою (2.37) розраховуємо статистику критерію 
:
.
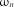Із табл. 2.11 для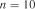 
знаходимо критичне значення 
.
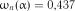142 |
Розділ 2 |
Так як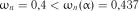 
, то гіпотеза експоненціальності розподілу інтервалів прибуття автомобілів підтверджується.
Критерій найбільшого інтервалу. Статистика критерію визна-
чається виразом
. (2.38)
Критичні значення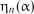 
на рівні значимості 
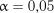наведені у табл. 2.12.
Таблиця 2.12
Критичні значенн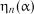я 
для 
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,975 |
8 |
0,561 |
24 |
0,235 |
3 |
0,871 |
9 |
0,477 |
30 |
0,198 |
4 |
0,768 |
10 |
0,445 |
40 |
0,158 |
5 |
0,684 |
12 |
0,392 |
60 |
0,113 |
6 |
0,616 |
15 |
0,335 |
120 |
0,063 |
7 |
0,561 |
20 |
0,270 |
|
|
Гіпотеза експоненціальності підтверджується у випадку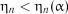 
.
Приклад 12. Перевірити гіпотезу експоненціальності розподілу для вихідних даних прикладу 8 на рівні значимості 
.
Розв’язок. Маємо 
, 
, 
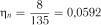. Із
табл. 2.12 визначаємо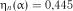 
. Так як 
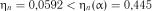, то гіпотеза експоненціальності розподілу підтверджується.
Критерій Хартлі. Це один з найбільш простих у обчислювальному відношенні критеріїв. Статистика критерію має вигляд
. (2.39)
Ідентифікація параметрів статистичними законами розподілу |
143 |
Критичні значення статистики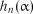 
на рівні значимості наведені у табл. 2.13.
Таблиця 2.13 Критичні значенн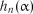я 
для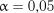 
|
|
|
|
|
|
|
|
|
|
|
|
2 |
39 |
6 |
266 |
10 |
505 |
3 |
88 |
7 |
333 |
11 |
626 |
4 |
142 |
8 |
403 |
12 |
704 |
5 |
202 |
9 |
475 |
|
|
|
|
|
|
|
|
При 
нульова гіпотеза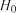 
відхиляється.
Приклад 13. Перевірити гіпотезу експоненціальності розподілу для вихідних даних прикладу 8 за критерієм Хартлі на рівні значимості 
.
Розв’язок. Маємо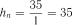 
. Для 
із табл. 2.13 маємо 
,
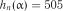що суттєво більше ніж отримане значення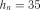 
. Отже, гіпотеза експоненціальності розподілу випадкової величини підтверджується.
2.4.2.2. Критерії перевірки для рівномірного розподілу. Якщо
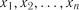– вибірка із розподілу імовірностей з функцією 
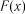, то випадкова величина 
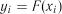розподілена рівномірно на інтервалі 
. Тому встановлення рівномірності розподілу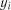 
є по суті критерієм згоди досліджуваних даних з теоретичним розподілом 
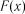. Для перевірки цього розподілу можна скористатися наступними критеріями.
Критерій Шермана. Статистика критерію для перевірки рівномірності розподілу має вигляд
, 
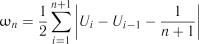, (2.40)
де |
– порядкова статистика, рівномірно розподілена на |
інтервалі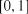 
.
144 |
Розділ 2 |
Критичні значення статистики наведені у табл. 2.14. Таблиця 2.14
Критичні значенн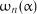я 
для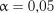 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,475 |
8 |
0,482 |
15 |
0,458 |
2 |
0,537 |
9 |
0,477 |
16 |
0,455 |
|
3 |
0,578 |
10 |
0,473 |
17 |
0,453 |
|
4 |
0,509 |
11 |
0,469 |
18 |
0,451 |
|
5 |
0,502 |
12 |
0,466 |
19 |
0,449 |
|
6 |
0,494 |
13 |
0,463 |
20 |
0,448 |
|
7 |
0,488 |
14 |
0,460 |
|
|
|
Якщо |
, |
нульова гіпотеза |
відхиляється. |
|||
Приклад 13. Маємо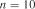 
спостережень величини транспортної партії вантажів у тоннах
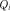: 0,5; 0,8; 1,2; 1,6; 2,5; 3,8; 4,6; 5,2; 6,3; 8,5.
Необхідно перевірити гіпотезу рівномірності розподілу даних вибірки на рівні значимості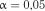 
.
Розв’язок. Перетворюємо вихідні дані у рівномірно розподілений ряд:
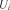: 0,0142; 0,0371; 0,0714; 0,1171; 0,1886; 0,2971; 0,4286; 0,5771; 0,7571; 1,00.
Обчислюємо статистику критерію Шермана:
Із табл. 2.14 для маємо |
. |
Так як |
, гіпотеза рівномірності розподілу підтвер- |
джується. |
|
Ідентифікація параметрів статистичними законами розподілу |
145 |
Критерій типу Колмогорова-Смірнова. Модифіковані фор-
мули критеріїв для задачі перевірки рівномірності розподілу ранжованої вибірки задаються статистиками
; |
; (2.41) |
; 
.
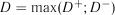Розподіл статистик буде швидко збігатися, якщо використати їх модифікації
; (2.42)
;
;
.
Гіпотеза рівномірності підтверджується у випадках
і ;
і .
На рівні значимості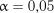 
критичні значення критеріїв рівномірності розподілу дорівнюють
Приклад 15. За даними прикладу 14 перевірити гіпотезу рівномірності розподілу величини транспортної партії на рівні значимості 
.
146 |
Розділ 2 |
Розв’язок. Результати обчислень окремих складових у формулах (2.41) наведені у таблиці.
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,5 |
0,0142 |
0,0909 |
–0,0767 |
0,9967 |
2 |
0,8 |
0,0371 |
0,1818 |
–0,1447 |
0,1447 |
3 |
1,2 |
0,0714 |
0,2727 |
–0,2013 |
0,2013 |
4 |
1,6 |
0,1171 |
0,3636 |
–0,2465 |
0,2465 |
5 |
2,5 |
0,1836 |
0,4545 |
–0,2709 |
0,2709 |
6 |
3,8 |
0,2971 |
0,5454 |
–0,2483 |
0,2483 |
7 |
4,6 |
0,4286 |
0,6363 |
–0,2077 |
0,2077 |
8 |
5,2 |
0,5771 |
0,7272 |
–0,1501 |
0,1501 |
9 |
6,3 |
0,7571 |
0,8181 |
–0,0610 |
0,0610 |
10 |
8,5 |
1,0000 |
0,9090 |
–0,0910 |
–0,0910 |
|
|
|
|
|
|
Визначаємо:
; 
; 
; 
;
;
;
;
.
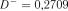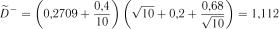Так як 
і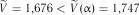 
, то гіпотеза рівномірності розподілу підтверджується.
Критерій Саркаді-Косіка. Статистика цього критерію визначається виразом
,(2.43)
Ідентифікація параметрів статистичними законами розподілу |
147 |
де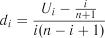 
; 
.
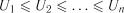Гіпотеза про рівномірність розподілу на рівні значимості 
підтверджується, якщо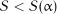 
. Критичні значення 
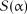наведені у табл. 2.15.
Таблиця 2.15
Критичні значенн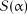я 
для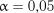 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,499 |
|
20 |
0,931 |
|
35 |
1,020 |
|
60 |
1,060 |
|
90 |
1,080 |
10 |
0,741 |
25 |
0,973 |
40 |
1,040 |
70 |
1,070 |
100 |
1,080 |
||||
15 |
0,881 |
30 |
1,000 |
50 |
1,050 |
80 |
1,070 |
|
|
|
|||
Приклад 16. За даними прикладу 14 перевірити гіпотезу рівномірності розподілу випадкової величини на рівні значимості 
за критерієм Саркаді-Косіка.
Розв’язок. Обчислення статистики критерію наведені у таблиці.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,0142 |
0,0909 |
–0,0767 |
10 |
–0,00767 |
0,5883∙10–4 |
2 |
0,0371 |
0,1818 |
–0,1447 |
18 |
–0,00804 |
0,6462∙10–4 |
3 |
0,0714 |
0,2727 |
–0,2013 |
24 |
–0,00839 |
0,7035∙10–4 |
4 |
0,1171 |
0,3636 |
–0,2465 |
28 |
–0,00880 |
0,7750∙10–4 |
5 |
0,1836 |
0,4545 |
–0,2709 |
30 |
–0,00903 |
0,8154∙10–4 |
6 |
0,2971 |
0,5454 |
–0,2483 |
30 |
–0,00828 |
0,6856∙10–4 |
7 |
0,4286 |
0,6363 |
–0,2077 |
28 |
–0,00742 |
0,5502∙10–4 |
8 |
0,5771 |
0,7272 |
–0,1501 |
24 |
–0,00625 |
0,3911∙10–4 |
9 |
0,7571 |
0,8181 |
–0,0610 |
18 |
–0,00339 |
0,1148∙10–4 |
10 |
1,0000 |
0,9090 |
–0,0910 |
10 |
–0,00910 |
0,8281∙10–4 |
|
|
|
|
|
–0,05817 |
6,0982∙10-4 |
Обчислюємо статистику |
|
. |
Із табл. 1.15 для |
визначаємо |
. |
Маємо |
, отже гіпотеза рівномірності розподілу вели- |
|
чини транспортної партії вантажів підтверджується.
Критерій Фроціні. Для перевірки рівномірності розподілу ранжованого ряду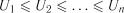 
на відрізку 
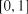використовується статистика
148 |
Розділ 2 |
. (2.44)
Критичні значення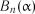 
на рівні значимості 
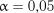наведені у табл. 2.16.
Таблиця 2.16
Критичні значенн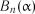я 
для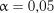 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,5756 |
|
9 |
0,5764 |
|
13 |
0,5815 |
6 |
0,5700 |
10 |
0,5723 |
14 |
0,5769 |
||
7 |
0,5780 |
11 |
0,5806 |
15 |
0,5730 |
||
8 |
0,5733 |
12 |
0,5790 |
|
|
0,5780 |
|
Приклад 17. За даними прикладу 14 перевірити гіпотезу рівномірності розподілу випадкової величини на рівні значимості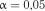 
за критерієм Фроціні.
Розв’язок. Обчислюємо статистику
Із табл. 2.16 для знаходимо |
. |
Так як |
, то гіпотеза рівномірності розподілу випадко- |
вої величини підтверджується. |
|
Критерій вибіркового розмаху. Статистика критерію обчислю-
ється за формулою
. (2.45)
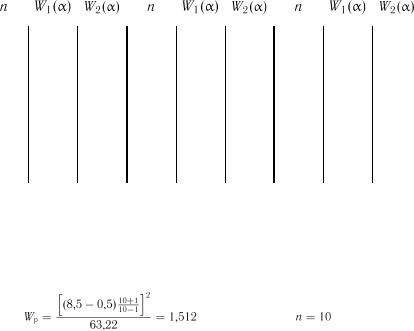
Тут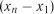 
– вибірковий розмах. Гіпотеза про рівномірність розподілу підтверджується, якщо 
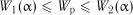. Критичні
Ідентифікація параметрів статистичними законами розподілу |
149 |
значення критерію 
та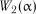 
на рівні значимості 
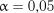наведені у табл. 2.17.
Таблиця 2.17
Критичні значення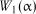 
та 
для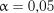 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
6,15 |
7,99 |
|
12 |
0,84 |
1,57 |
|
21 |
0,47 |
0,81 |
4 |
3,44 |
5,43 |
13 |
0,77 |
1,42 |
22 |
0,45 |
0,78 |
||
5 |
2,42 |
4,18 |
14 |
0,71 |
1,31 |
23 |
0,43 |
0,73 |
||
6 |
1,88 |
3,41 |
15 |
0,66 |
1,21 |
24 |
0,42 |
0,70 |
||
7 |
1,54 |
2,85 |
16 |
0,62 |
1,11 |
25 |
0,40 |
0,67 |
||
8 |
1,32 |
2,47 |
17 |
0,58 |
1,04 |
30 |
0,33 |
0,54 |
||
9 |
1,15 |
2,19 |
18 |
0,55 |
0,98 |
40 |
0,25 |
0,39 |
||
10 |
1,02 |
1,92 |
19 |
0,52 |
0,92 |
50 |
0,20 |
0,30 |
||
11 |
0,92 |
1,73 |
20 |
0,50 |
0,86 |
|
|
|
|
|
Приклад 18. За даними прикладу 14 перевірити гіпотезу рівномірності розподілу випадкової величини на рівні значимості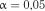 
за критерієм вибіркового розмаху.
Розв’язок. Маємо
; 
; 
; 
.
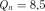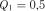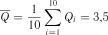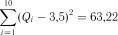Тоді |
. Із табл. 2.17 для визначаємо кри- |
тичні значення критерію вибіркового розмаху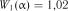 
і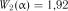 
. Так як
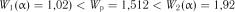, то гіпотеза про рівномірність розподілу випадкової величини підтверджується.
2.4.2.3. Критерії перевірки для логарифмічно-нормального роз-
поділу. При обчисленнях, пов’язаних з логарифмічно-нормальним розподілом, використовують прийом для нормального розподілу, замінюючи при цьому значення випадкової величини її логарифмом. Перевірку логарифмічно-нормального розподілу можна здійснювати за такими критеріями: