big_doc_LKG
.pdf
Формування вихідної інформації для аналізу і дослідження систем |
61 |
.
Так як 
, то найменше за значенням спостереження також
не є викидом.
1.4.1.2. Критерій Ірвіна. Статистика критерію має вигляд:
– для перевірки підозрілого найбільшого значення 
; |
(1.57) |
– для перевірки підозрілого найменшого значення 
. (1.58)
При 
найбільше (найменше) значення вважається викидом на рівні значимості 
. Критичні значення 
критерію Ірвіна наведені в табл. 1.20.
Таблиця 1.20
Критичні значення критерію Ірвіна для
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2,77 |
30 |
1,20 |
70 |
1,05 |
200 |
0,95 |
3 |
2,17 |
40 |
1,15 |
80 |
1,04 |
300 |
0,91 |
10 |
1,46 |
50 |
1,11 |
90 |
1,03 |
400 |
0,87 |
20 |
1,27 |
60 |
1,08 |
100 |
1,02 |
500 |
0,83 |
|
|
|
|
|
|
|
|
Приклад 16. Перевірити гіпотезу про наявність викидів за даними прикладу 15 за критерієм Ірвіна при рівні значимості 
.
Розв’язок. Обчислюємо статистики Ірвіна:
– для найбільшого значення
;
– для найменшого значення
.
62 |
Розділ 1 |
Із таблиці критичних значень критерію Ірвіна (табл. 1.20) для 
маємо 
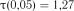. Так як 
, то мінімальне та максимальне значення вибірки 
та 
не є викидами.
1.4.1.3. Критерій найбільшого абсолютного відхилення. Для ви-
ділення аномального значення випадкової величини обчислюється значення статистики
. (1.59)
Якщо 
, значення 
вважається викидом. Критичні зна-
чення критерію найбільшого абсолютного відхилення |
для довір- |
чої імовірності 
(
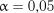) наведені в табл. 1.21.
Таблиця 1.21 Критичні значення 
критерію найбільшого абсолютного
відхилення для 
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1,414 |
9 |
2,349 |
20 |
2,779 |
4 |
1,710 |
10 |
2,414 |
22 |
2,823 |
5 |
1,917 |
12 |
2,519 |
24 |
2,862 |
6 |
2,067 |
14 |
2,602 |
26 |
2,897 |
7 |
2,182 |
16 |
2,670 |
28 |
2,929 |
8 |
2,273 |
18 |
2,718 |
30 |
2,958 |
Критичне значення 
при 
можна апроксимувати такою залежністю
(1.60)
Приклад 17. Перевірити гіпотезу про наявність викидів за даними прикладу 15 за критерієм найбільшого абсолютного відхилення при рівні значимості 
.
Розв’язок. Обчислюємо значення статистики критерію найбільшого абсолютного відхилення
Формування вихідної інформації для аналізу і дослідження систем |
63 |
.
За таблицею критичних значень критерію (табл. 1.21) для 
знаходимо 
. Значення 
. Отже, гіпотеза про наявність викидів відхиляється.
Обчислимо також апроксимацію за формулою (1.60)
,
що приблизно дорівнює табличному значенню.
1.4.1.4. Критерій Груббса. Виявлення викидів базується на таких статистиках:
– для підозрілого найбільшого значення 
; |
(1.61) |
– для підозрілого найменшого значення 
. (1.62)
У випадку 
або 
відповідні значення ви-
падкової величини (
за 
та 
за 
) вважаються викидами. Критичні значення критерію Груббса 
і 
для довірчої
ймовірності 
наведені в табл. 1.22.
Таблиця 1.22
Критичні значення 
і 
критерію Груббса для довірчої імовірності 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1,738 |
1,412 |
9 |
2,392 |
2,237 |
15 |
2,617 |
2,493 |
21 |
2,750 |
2,644 |
4 |
1,941 |
1,689 |
10 |
2,441 |
2,294 |
16 |
2,644 |
2,523 |
22 |
2,768 |
2,664 |
5 |
2,080 |
1,869 |
11 |
2,484 |
2,343 |
17 |
2,668 |
2,551 |
23 |
2,784 |
2,683 |
6 |
2,184 |
1,996 |
12 |
2,523 |
2,387 |
18 |
2,691 |
2,577 |
24 |
2,800 |
2,701 |
7 |
2,267 |
2,093 |
13 |
2,557 |
2,426 |
19 |
2,712 |
2,600 |
25 |
2,815 |
2,717 |
|
|
|
|
|
|
|
|
|
|
|
|
64 |
Розділ 1 |
8 2,334 2,172 
14 2,589 2,461 
20 2,732 2,623 
За невеликого обсягу вибірки (
) критичні значення критерію Груббса 
можна обчислити, використовуючи таке наближення
, |
(1.63) |
де 
– 
-квантиль стандартного нормального розподілу, яка об-
числюється за формулою 
.
Для 
при 
може бути використана апроксимація
(1.64)
Приклад 18. Перевірити гіпотезу про наявність викидів за даними прикладу 15 за критерієм Груббса при рівні значимості 
.
Розв’язок. Обчислюємо статистики критерію Груббса:
; |
. |
Із таблиці критичних точок критерію Груббса (табл. 1.22) для 
і 
знаходимо 
і 
. Так як 
та 
, гіпотеза про наявність викидів у вибірці відхиляється.
Скористаємося апроксимацією для 
,
що приблизно дорівнює табличному значенню.
1.4.1.5. Критерій Тітьєна-Мура для виявлення декількох викидів.
При використанні цього критерію можливі два випадки.
Випадок 1. Підозрілими є найбільше або найменше спостереження. У цьому випадку використовуються такі статистики:
– для виокремлення 
найбільших спостережень
Формування вихідної інформації для аналізу і дослідження систем |
65 |
, |
(1.65) |
де |
і |
; |
– для виокремлення 
найменших спостережень
, |
(1.66) |
де 
.
Наявність викидів вважається значимою з довірчою імовірністю 
при виконанні умови
.
Критичні значення 
для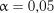 
(
) наведені в табл. 1.23.
Випадок 2. Підозрілими є як найменші, так і найбільші спостереження. Для їх виявлення використовується таке правило.
Визначаються абсолютні відхилення |
|
і ранжуються за |
||
збільшенням від |
до |
. Позначимо через |
вибіркове значення |
|
, для якого |
є -тим за величиною. |
|
|
|
Для перевірки гіпотези виключення |
найбільших за модулем |
|||
спостережень використовується статистика |
|
|
||
66 |
Розділ 1 |
, |
(1.67) |
де 
.
Формування вихідної інформації для аналізу і дослідження систем |
67 |
Таблиця 1.23 Критичні значення 
(
) для довірчої імовірності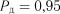 
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
30,003
40,051 0,001
50,125 0,018
60,203 0,055 0,010
70,273 0,106 0,032
80,326 0,146 0,064 0,022
90,372 0,194 0,099 0,045
100,418 0,233 0,129 0,070 0,034
110,454 0,270 0,162 0,098 0,054
120,489 0,305 0,196 0,125 0,076 0,042
130,517 0,337 0,224 0,150 0,097 0,060
140,540 0,363 0,250 0,174 0,122 0,079 0,050
150,556 0,387 0,276 0,197 0,140 0,097 0,066
160,579 0,410 0,300 0,219 0,159 0,115 0,082 0,055
170,594 0,427 0,322 0,240 0,181 0,136 0,100 0,072
18 |
0,608 |
0,447 |
0,337 |
0,259 |
0,200 |
0,154 |
0,116 |
0,086 |
0,062 |
|
19 |
0,624 |
0,462 |
0,354 |
0,277 |
0,209 |
0,168 |
0,130 |
0,099 |
0,074 |
|
20 |
0,639 |
0,484 |
0,377 |
0,299 |
0,238 |
0,188 |
0,150 |
0,115 |
0,088 |
0,066 |
25 |
0,696 |
0,550 |
0,450 |
0,374 |
0,312 |
0,262 |
0,222 |
0,184 |
0,154 |
0,126 |
30 |
0,730 |
0,599 |
0,506 |
0,434 |
0,376 |
0,327 |
0,283 |
0,245 |
0,212 |
0,183 |
35 |
0,762 |
0,642 |
0,554 |
0,482 |
0,424 |
0,376 |
0,334 |
0,297 |
0,264 |
0,235 |
40 |
0,784 |
0,672 |
0,588 |
0,523 |
0,468 |
0,378 |
0,378 |
0,342 |
0,310 |
0,280 |
45 |
0,802 |
0,696 |
0,618 |
0,556 |
0,502 |
0,417 |
0,417 |
0,382 |
0,350 |
0,320 |
50 |
0,820 |
0,722 |
0,646 |
0,588 |
0,535 |
0,450 |
0,450 |
0,414 |
0,383 |
0,356 |
За умови |
спостереження вважають викидами. Кри- |
тичні значення критерію |
для довірчої імовірності |
наведені в табл. 1.24. |
|
68 |
Розділ 1 |
Таблиця 1.24
Критичні значення 
для довірчої ймовірності 
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
30,001
40,025 0,001
50,081 0,010
60,146 0,034 0,004
70,208 0,065 0,016
80,265 0,099 0,034 0,010
90,314 0,137 0,057 0,021
100,356 0,172 0,083 0,037 0,014
110,386 0,204 0,107 0,055 0,026
120,424 0,234 0,133 0,073 0,039 0,018
130,455 0,262 0,156 0,092 0,053 0,028
140,484 0,293 0,179 0,112 0,068 0,039 0,021
150,509 0,317 0,206 0,134 0,084 0,052 0,030
16 |
0,526 |
0,340 |
0,227 |
0,153 |
0,102 |
0,067 |
0,041 |
0,024 |
|
|
17 |
0,544 |
0,362 |
0,248 |
0,170 |
0,116 |
0,078 |
0,050 |
0,032 |
|
|
18 |
0,562 |
0,382 |
0,267 |
0,187 |
0,132 |
0,091 |
0,062 |
0,041 |
0,026 |
|
19 |
0,581 |
0,398 |
0,287 |
0,203 |
0,146 |
0,105 |
0,074 |
0,050 |
0,033 |
|
20 |
0,597 |
0,416 |
0,302 |
0,221 |
0,163 |
0,119 |
0,085 |
0,059 |
0,041 |
0,028 |
25 |
0,652 |
0,493 |
0,381 |
0,298 |
0,236 |
0,186 |
0,146 |
0,114 |
0,089 |
0,068 |
30 |
0,698 |
0,549 |
0,443 |
0,364 |
0,298 |
0,246 |
0,203 |
0,166 |
0,137 |
0,112 |
35 |
0,732 |
0,596 |
0,495 |
0,417 |
0,351 |
0,298 |
0,254 |
0,214 |
0,171 |
0,154 |
40 |
0,758 |
0,629 |
0,534 |
0,458 |
0,395 |
0,343 |
0,297 |
0,259 |
0,223 |
0,195 |
45 |
0,778 |
0,658 |
0,577 |
0,492 |
0,433 |
0,381 |
0,337 |
0,299 |
0,263 |
0,233 |
50 |
0,797 |
0,684 |
0,599 |
0,529 |
0,468 |
0,417 |
0,373 |
0,334 |
0,299 |
0,268 |
Приклад 19. Застосуємо критерій Тітьєна-Мура при рівні значимості 
для перевірки наявності декількох викидів у статистичній вибірці прикладу 15.
Розв’язок.
Випадок 1. Підозрілими вважаємо окремо найбільші або найменші спостереження у вибірці.
Для найбільших спостережень (
і 
) маємо:
Формування вихідної інформації для аналізу і дослідження систем |
69 |
; 
;
; 
;
; 
.
Обчислюємо статистики:
|
|
|
; |
|
|
|
|
. |
Із табл. 1.23 для |
( , |
|
) знаходимо |
|
, для |
|
||
маємо |
. |
Так як |
|
|
, |
найбільше |
значення |
|
не вважаємо викидом. Так як |
|
|
, |
найбільше |
||||
значення |
також не є викидом. |
|
|
|
|
|
||
Для найменших спостережень ( |
, |
) маємо: |
|
|
|
|
||
|
|
|
; |
|
|
; |
|
|
|
|
|
; |
|
|
. |
|
|
Обчислюємо статистики: |
|
|
|
|
|
|
||
|
|
; |
|
|
|
. |
|
|
Так як |
|
|
і |
|
|
, обидва най- |
||
менші спостереження не повинні вважатися викидами. |
|
|
|
|
||||
Випадок 2. Підозрілими вважаємо найбільше ( |
) |
і найменше ( |
) |
|||||
спостереження. |
|
|
|
|
|
|
|
|
Послідовно |
розраховуємо |
|
: |
|
|
|
; |
|
|
|
… |
|
|
|
. Утворюємо |
||
ранжований ряд за зростанням величини . |
|
|
|
|
|
|||
70 |
Розділ 1 |
Результати зводимо в таблицю, в якій у відповідних стовпчиках вказані:
1)номери спостережень 
;
2)ранжовані значення величини 
;
3)ранги 
величин 
, що відповідають значенням 
;
4)величини 
, що дорівнюють вибірковому значенню 
для 
-го за величиною значення 
.
1 |
0,5 |
11 |
26 |
2 |
2,5 |
12 |
28 |
3 |
4,5 |
13 |
30 |
4 |
5,5 |
10 |
20 |
5 |
6,5 |
14 |
32 |
6 |
9,5 |
9 |
16 |
7 |
9,5 |
15 |
35 |
8 |
10,5 |
7 |
15 |
9 |
10,5 |
8 |
15 |
10 |
11,5 |
6 |
14 |
11 |
13,5 |
5 |
12 |
12 |
14,5 |
4 |
11 |
13 |
14,5 |
16 |
40 |
14 |
17,5 |
3 |
8 |
15 |
18,5 |
17 |
44 |
16 |
19,5 |
2 |
6 |
17 |
23,5 |
1 |
2 |
18 |
24,5 |
18 |
50 |
19 |
26,5 |
19 |
52 |
20 |
28,5 |
20 |
54 |
Вибираємо із таблиці два (
) найбільших спостереження (
і 
) і для них обчислюємо:
; |
; |
; |
; |
; |
. |
Обчислюємо статистики: |
|
|
; |
|
. |
Із табл. 1.24 для 
(
, 
) визначаємо 
і відповідно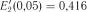 
.
Так як 
і 
, обидва перевірені спостереження (
і 
) не вважаються викидами.
1.4.1.6. Критерій Роспера для виявлення декількох викидів. Цей метод передбачає не тільки виокремлювання самих викидів, а і виявлення їх кількості. Алгоритм критерію Роспера полягає у наступному.
За початковою вибіркою об’ємом 
обчислюються значення 
, 
і статистика крайніх (максимального і мінімального) спостережень ранжованого ряду