big_doc_LKG
.pdf
Формування вихідної інформації для аналізу і дослідження систем |
51 |
. (1.49)
Значення 
розраховуються за формулами:
(1.50)
Якщо 
, то на рівні значимості 
гіпотеза нормальності
підтверджується.
Приклад 12. Статистичні дані величини вхідного вантажопотоку на вантажний пункт підприємства представлені трьома (
) ранжованими вибірками по шість (
) спостережень у кожній.
Номер |
|
Величина вантажопотоку в |
-му спостереженні , т |
|||||
вибірки |
1 |
2 |
3 |
4 |
|
5 |
6 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
20 |
2 |
|
|
|
|
|
|
|
40 |
3 |
|
|
|
|
|
|
|
24 |
Необхідно перевірити гіпотезу про нормальний розподіл випадкової величини вхідного вантажопотоку з довірчою імовірністю 
за критерієм Саркаді.
Розв’язок. Для першої вибірки обчислюємо величини 
(
):
; |
; |
. |
52 |
Розділ 1 |
Обчислюємо величини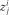 
(
):
Далі для кількості ступенів вільності |
в додатку Д4 знаходимо зна- |
|
чення функції |
і обчислюємо величини |
: |
|
; |
; |
|
|
; |
|
; |
; |
|
|
; |
|
; |
; |
|
|
; |
|
; |
. |
Формування вихідної інформації для аналізу і дослідження систем |
53 |
Величину 
обчислюємо за формулою (1.48). Із додатка Д4 маємо для 
. Тоді
.
Аналогічні розрахунки проводимо для другої і третьої вибірок. В результаті отримуємо:
–друга вибірка:
; 
; 
; 
; 
;
; 
; 
; 
;
; 
; 
; 
;
; |
; |
; |
; |
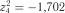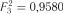–третя вибірка:
; 
; 
; 
; 
;
; 
; 
; 
;
; 
; 
; 
;
; |
; |
; |
. |
Обчислюємо статистики «гладкого критерію» Неймана:
–перша вибірка:
;
;
54 |
Розділ 1 |
; 
; 
; 
;
; |
; |
; |
; |
; 
; 
; 
.
Аналогічним чином обчислюємо статистики для другої та третьої вибірок. Результати розрахунків зводимо в підсумкову таблицю.
Результати обчислення статистик
Стати- |
Перша вибірка |
Друга вибірка |
Третя вибірка |
|
|
|||||||||
стики |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
–1,412 |
–1,550 |
–1,219 |
–1,623 |
–1,588 |
–1,586 |
–1,583 |
–1,146 |
–1,584 |
–1,630 |
–1,091 |
–1,030 |
– |
|
|
1,111 |
1,565 |
0,544 |
1,828 |
1,699 |
1,699 |
1,686 |
0,350 |
1,646 |
1,847 |
0,213 |
|
0,089 |
– |
|
–0,347 |
–1,189 |
0,487 |
–1,725 |
–1,377 |
–1,450 |
–1,416 |
0,710 |
–1,447 |
–1,768 |
0,849 |
|
0,953 |
– |
|
–0,555 |
–0,546 |
–1,221 |
1,371 |
0,957 |
0,915 |
0,864 |
–1,283 |
0,788 |
1,470 |
–1,275 |
–1,224 |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,994 |
2,403 |
1,486 |
2,634 |
2,521 |
2,515 |
2,506 |
1,313 |
2,509 |
2,657 |
1,190 |
|
1,061 |
24,79 |
|
1,234 |
2,449 |
0,296 |
3,342 |
2,887 |
2,887 |
2,843 |
0,123 |
2,709 |
3,411 |
0,045 |
|
0,008 |
22,23 |
|
0,120 |
1,414 |
0,237 |
2,976 |
1,896 |
2,102 |
2,005 |
0,504 |
2,094 |
3,126 |
0,721 |
|
0,908 |
18,10 |
|
0,308 |
0,298 |
1,491 |
1,880 |
0,916 |
0,837 |
0,746 |
1,646 |
0,621 |
2,161 |
1,626 |
|
1,498 |
14,03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
79,15 |
Обчислюємо статистику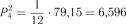 
. Критичне значення 
з
кількістю ступенів вільності 
знаходимо із додатку Д3 
. Так як
, то гіпотеза про нормальність розподілу випадкових величин підтверджується.
1.3.3.3. Критерій Смірнова. Розглядається 
(
) незалежних вибірок, кожна із яких має однакову кількість спостережень 
(
).
При 
для перевірки нормальності розподілу використовується статистика
, |
(1.51) |
де 
– навмання взяте 
-те спостереження в 
-ій вибірці;
– середнє вибіркове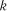 
-ої вибірки;
Формування вихідної інформації для аналізу і дослідження систем |
55 |
– стандартне відхилення 
-тої вибірки.
При 
переходять до статистики
. (1.52)
При 
статистика 
має рівномірний розподіл, а при 
статистика 
має 
-розподіл Стьюдента (додаток Д4) з 
ступенями вільності. Перевірка гіпотези нормальності за обчисленими значеннями величин 
i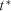 
виконується за допомогою критерію згоди 
у такій послідовності.
1. Із кожної вибірки беремо навмання по одному значенню випадкової величини. Якщо вибірка представляє часові «проби», взяті із поточних спостережень виробничого процесу (величина поточної транспортної партії вантажів, що надходять на склад; тривалість наван- таження-розвантаження наступного транспортного засобу; час обертання автомобіля на маятниковому маршруті при виконанні чергової їздки; поточне завантаження транспортного засобу тощо), то можна із кожної проби взяти по одному першому (або останньому) за часом порядковому спостереженню. Порядок відбору не має суттєвого значення: важливим є те, щоб відбір одного спостереження із даної проби здійснювався без будь-якого обліку значень випадкових величин, що відбираються із інших проб. Кількість спостережень у кожній вибірці повинна бути однаковою для всіх вибірок, тобто 
.
Якщо в кожній вибірці число 
є достатньо великим (наприклад, 
), то можна виконати не одну, а дві або навіть три (при великих 
) самостійні перевірки гіпотези, наприклад, за першим і останнім екземплярами кожної проби.
2. Для кожного відібраного значення обчислюється показник 
за формулою (1.51) при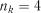 
, або показник 
за формулою (1.52) при 
. Після цього з отриманих значень 
або 
утворюють варіаційний ряд і для кожного значення підраховується емпірична функція розподілу статистики 
за формулою
56 |
Розділ 1 |
, |
(1.53) |
де 
– кількість розглядуваних вибірок.
3. Для кожного відібраного значення статистики 
(
або 
) обчислюється теоретична функція розподілу 
.
При 
спостереження у вибірці розподіл емпіричного показника 
підпорядковується рівномірному розподілу із щільністю
. (1.54)
При 
теоретична функція розподілу 
визначається за допомогою функції розподілу Стьюдента (додаток Д4).
4. Обчислюють величину 
за формулою
. (1.55)
5. Визначають критичну точку 
. Для рівня значимості
.
6. Порівнюють величини 
та 
. Якщо 
, то гіпотеза про нормальний розподіл розглядуваних сукупностей відхиляється як така, що не відповідає результатам спостережень.
Приклад 13. Щоденно на вантажному терміналі вантажопереробки і постачання промислових товарів формуються партії вантажу для доставки чотирьом (
) філіям деякої торговельної фірми. За даними проведених спостережень (табл. 1.15) протягом десяти (
) часових проб (днів) перевірити гіпотезу нормальності розподілу тривалості формування однієї партії вантажу за критерієм Смірнова.
Розв’язок. Беремо із кожної проби (для одного дня) по одній партії (першу за часом формування) і обчислюємо для кожного із 10 значень показник 
. Результати обчислень зводимо в розрахункову таблицю показника 
(табл. 1.15).
В стовпчику 1 проставлені номери поточної проби (дня), а в стовпчиках 2–5 дані тривалості формування кожної із чотирьох партій товарів по десяти пробах.
Формування вихідної інформації для аналізу і дослідження систем |
57 |
Таблиця 1.15
Розрахункова таблиця показника 
Номер
проби (дня)
Тривалість формування у порядку проведених спостережень, год.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
1 |
0,98 |
0,52 |
0,10 |
0,42 |
0,505 |
0,364 |
0,475 |
1,305 |
2 |
0,43 |
0,26 |
0,86 |
0,78 |
0,582 |
0,286 |
–0,152 |
–0,531 |
3 |
0,19 |
0,97 |
0,73 |
0,63 |
0,630 |
0,326 |
–0,440 |
–1,350 |
4 |
0,57 |
0,31 |
0,26 |
0,20 |
0,335 |
0,163 |
0,235 |
1,442 |
5 |
0,35 |
0,27 |
0,24 |
0,18 |
0,260 |
0,071 |
0,090 |
1,268 |
6 |
0,90 |
1,58 |
0,65 |
1,36 |
1,122 |
0,436 |
–0,222 |
–0,509 |
7 |
1,57 |
0,82 |
1,65 |
1,63 |
1,418 |
0,397 |
0,152 |
0,383 |
8 |
0,64 |
0,95 |
0,25 |
0,71 |
0,638 |
0,289 |
0,002 |
0,007 |
9 |
0,32 |
0,79 |
0,40 |
0,66 |
0,542 |
0,219 |
–0,222 |
–1,014 |
10 |
1,40 |
0,30 |
0,27 |
0,60 |
0,642 |
0,527 |
0,758 |
1,438 |
Встовпчиках 6 і 7 записані середнє арифметичне 
і стандартне відхилення 
.
Встовпчику 9 показані значення показника 
, обчислені за першим із спостережних значень кожної проби.
З отриманих значень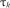 
(
) формуємо варіаційний ряд і обчислюємо для кожної точки значення емпіричної функції розподілу 
і теоретичної функції 
для подальшого підрахунку величини 
. Всі обчислення зводимо у розрахункову таблицю (табл. 1.16).
|
|
|
|
|
|
Таблиця 1.16 |
|
Розрахункова таблиця складових для обчислення величини |
|
||||
|
|
|
|
|
|
|
№ |
|
|
|
|
|
|
проби |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
6 |
|
|
|
|
|
|
|
1 |
–1,350 |
0,110 |
0,05 |
0,06 |
|
0,0036 |
2 |
–1,014 |
0,208 |
0,15 |
0,057 |
|
0,0033 |
3 |
–0,531 |
0,347 |
0,25 |
0,097 |
|
0,0094 |
4 |
–0,509 |
0,353 |
0,35 |
0,003 |
|
0,0000 |
5 |
0,007 |
0,502 |
0,45 |
0,052 |
|
0,0027 |
6 |
0,383 |
0,611 |
0,55 |
0,061 |
|
0,0037 |
7 |
1,268 |
0,866 |
0,65 |
0,216 |
|
0,0466 |
8 |
1,305 |
0,877 |
0,75 |
0,127 |
|
0,0161 |
9 |
1,438 |
0,915 |
0,85 |
0,065 |
|
0,0042 |
10 |
1,442 |
0,916 |
0,95 |
0,034 |
|
0,0012 |
58 |
Розділ 1 |
= 0,0908
В стовпчику 2 цієї таблиці розташовані обчислені в попередній таблиці показники 
для кожної проби у порядку збільшення їх значень. В стовпчик 3 записані теоретичні значення функції розподілу 
, обчислені за формулою (1.54) для відповідних значень 
.
В стовпчику 4 містяться значення емпіричної функції розподілу 
, розраховані за формулою (1.53). Так, наприклад, для 5-го за чергою значення 
маємо
.
У стовпчику 5 показані різниці значень 
і в стовпчику 6 – квадрати цих різниць.
Підставивши у формулу (1.55) значення 
і підсумок значень у стовпчику 6 табл. 1.16, отримуємо
.
Так як значення 
, то гіпотеза про нормальний розподіл величини тривалості формування партії вантажу за даними спостережень підтвер-
джується.
Приклад 14. Перевірити гіпотезу про нормальність розподілу тривалості формування однієї вантажної партії товарів за критерієм Смірнова при 
і 
(табл. 1.17).
Розв’язок. Розрахунок показника 
показаний у табл. 1.17.
Таблиця 1.17
Розрахункова таблиця показника
Номер проби
1
2
3
4
5
Тривалість формування у порядку проведення спостережень
0,98 |
0,52 |
0,10 |
0,42 |
0,31 |
0,82 |
0,525 |
0,326 |
0,455 |
1,396 |
1,948 |
1,384 |
0,43 |
0,26 |
0,86 |
0,78 |
0,60 |
0,30 |
0,538 |
0,250 |
–0,108 |
–0,432 |
0,187 |
–0,340 |
0,19 |
0,97 |
0,73 |
0,63 |
1,40 |
0,40 |
0,720 |
0,428 |
–0,530 |
–1,238 |
1,533 |
–1,152 |
0,57 |
0,31 |
0,26 |
0,20 |
0,82 |
0,71 |
0,478 |
0,257 |
0,092 |
0,358 |
0,128 |
0,281 |
0,35 |
0,27 |
0,24 |
0,18 |
0,64 |
0,66 |
0,390 |
0,209 |
–0,040 |
–0,191 |
0,037 |
–0,148 |
|
|
|
|
|
|
|
|
|
|
|
|
Формування вихідної інформації для аналізу і дослідження систем |
59 |
В наступній розрахунковій табл. 1.18 обчислюємо складові для розрахунку 
. Величину 
визначаємо за додатком Д4 для числа ступенів вільності
.
|
|
|
|
|
|
|
|
Таблиця 1.18 |
|
Розрахункова таблиця складових для обчислення величини |
|
||||||
|
|
|
|
|
|
|
|
|
Номер |
|
|
|
|
|
|
|
|
проби |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
–1,152 |
|
0,842 |
0,10 |
0,742 |
|
0,551 |
2 |
|
–0,340 |
|
0,624 |
0,30 |
0,324 |
|
0,105 |
3 |
|
–0,148 |
|
0,556 |
0,50 |
0,056 |
|
0,003 |
4 |
|
0,281 |
|
0,603 |
0,70 |
–0,097 |
|
0,009 |
5 |
|
1,384 |
|
0,880 |
0,90 |
0,020 |
|
0,000 |
|
|
|
|
|
|
|
|
= 0,695 |
Обчислюємо значення |
: |
|
|
|
|
|||
|
|
|
|
|
|
. |
|
|
Так як 
, то гіпотеза про нормальний розподіл величини тривалості формування однієї партії вантажу відхиляється.
1.4. Виключення грубих аномальних значень випадкової величини
Ця задача пов’язана з тим, що статистична інформація, як правило, є неоднорідною. Поряд з основним масивом прямих спостережень або вимірів в експериментальних даних часто присутні грубі похибки, викликані прорахунками спостерігача, зробленими при введені в ЕОМ тощо. Без аналізу якості статистичних даних, усунення або зменшення впливу аномальних значень випадкових величин на результати наступних етапів опрацювання статистичної сукупності можна зробити помилкові висновки щодо досліджуваного об’єкта або явища.
Грубими аномальними вважаються такі дані, які значній мірі відрізняються від інших даних варіаційного ряду. При проведенні попереднього статистичного аналізу для відсіву грубих похибок можна використати декілька методів, заснованих на порівнянні максимального відносного відхилення випадкової величини від критичного значення деякого критерію.
60 |
Розділ 1 |
Розглянемо найбільш розповсюджені з точки зору практичного використання критерії.
1.4.1. Нормальний розподіл статистичних даних
1.4.1.1. Критерій Шовене. Згідно з цим критерієм елемент вибірки 
об’ємом 
є викидом, якщо ймовірність його відхилення від середнього значення не перевищує 
). Статистика Шовене розраховується за формулою
. (1.56)
Отримане значення 
порівнюється з критичним значенням 
статистики Шовене (табл. 1.19).
Таблиця 1.19
Критичні значення статистики Шовене
|
4 |
5 |
6 |
10 |
15 |
25 |
50 |
100 |
300 |
|
1,54 |
1,65 |
1,73 |
1,96 |
2,13 |
2,33 |
2,57 |
2,81 |
3,14 |
Якщо 
, то значення 
(
) вважається викидом і виключається із вибірки.
Приклад 15. Кількість вантажів, що надходять на склад в критих вагонах, представлена ранжованою вибіркою з 
спостережень:
: 2, 6, 8, 11, 12, 14, 15, 16, 20, 26, 28, 30, 32, 35, 40, 44, 50, 52, 54.
Необхідно перевірити наявність викидів у вибірці за критерієм Шовене.
Розв’язок. Розраховуємо вибіркові характеристики 
; 
. Для найбільшого за значенням спостереження (
) обчислюємо за формулою (1.56) статистику Шовене
.
За таблицею критичних значень статистики Шовене (табл. 1.19) для 
має-
мо 
. Так як 
, то 
не є викидом.
Перевіряємо найменше значення у вибірці (
)