§ 12.4. Торможенный откат

Расчет торможенного отката заключается в определении дей­ствительной скоростии путиоткатных частей. Движение откатных частей при торможенном откате рассматри­вается по тем же периодам, как и при свободном откате.

В первом и втором периодах дифференциальное уравнение дви­жения откатных частей имеет вид

в третьем, так как. Для определения скоро­

сти отката проинтегрируем уравнение (12.47):

Так как по зависимостям свободного отката

то

Имея в виду, что

или

Так как

то

откуда

В начале первого периода; тогда для

первого периода выражения (12.48) и (12.49) примут вид

В начале второго периодатогда для второго периода будем иметь

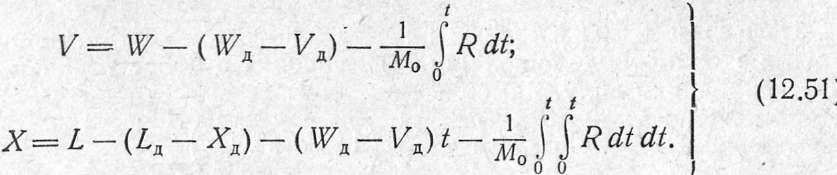
Полученные выражения (12.50) и (12.51) называются форму­лами перехода от элементов свободного отката к элементам тор-

Рис. 12.14. График силы R=f(t)

моженного отката. Для получения расчетных формул необходимо знать закон изменения силы сопротивления откату, кото­

рым обычно задаются. Выбранный закон зависит от конкретного типа орудия (полевого, зенитного, стационарного и т. д.).

Для полевых орудий закондолжен отвечать следую­

щим основным требованиям:

• значение силы сопротивления откату на любом участке от­ката не должно превосходить значениеполученное из усло­вия устойчивости орудия (рис. 12.6);

• торможение должно быть плавным, а энергия откатных ча­стей должна полностью поглощаться на заданной длине отката X.

Наиболее полно физической сущности явления отвечает закон проф. Е. Л. Бравина, получивший поэтому широкое распростране­ние (рис. 12.14). Закон удобен для интегрирования и позволяет применить для расчета элементов отката формулы перехода.

В первом периоде

поэтому закон носит краткое название «закона квадрата синуса».

Во втором периодеВ третьем периоде

изменяется линейно отимеет криволинейную

зависимость).

Первый период. Для расчета элементов торможенного от­ката в этом периоде закон (12.52) приводят к более удобному для интегрирования виду. Заменив

и обозначив через

получим

После подстановки R в формулы перехода (12.50) получим

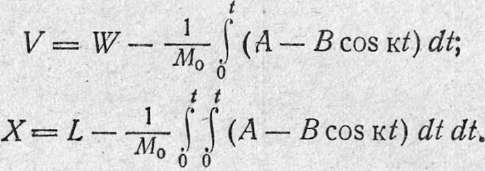
Путем интегрирования находим искомые величины: 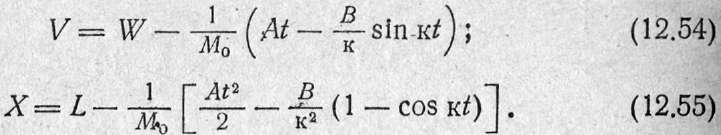В конце период

После подстановки этих значений в формулы (12.54) и (12.55) будем иметь:

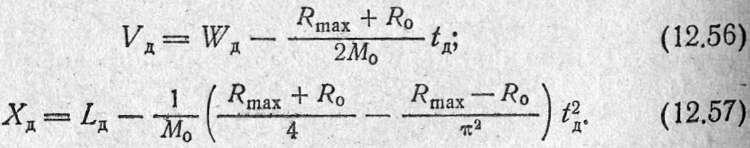
Если принятьто

Для производства расчетов необходимо знать величиныикоторые выбираются из следующих соображений. В началь­ный момент времени, когда откатные части неподвижны,сила гид­равлического тормоза отката будет равна нулю. Силасклады­вается в этом случае из следующих величин:

где—начальная сила накатника;

— сила трения;

— составляющая веса откатных частей, направленная вдоль оси канала ствола (рис. 12.15).

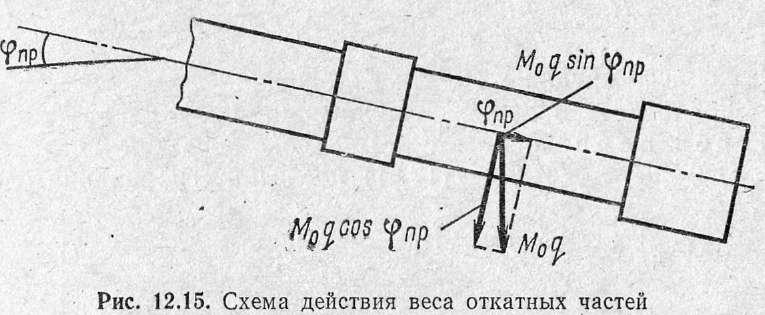
v

Начальная сила накатника, как будет показано ниже в гл. 13, определяется по формуле

где—наибольший угол возвышения;

— коэффициент трения на направляющих люльки;

— коэффициент учета трения в уплотнениях про­тивооткатных устройств.

Значение коэффициента v можно приближенно рассчитать по формуле проф. А. А. Толочкова

где d — калибр, см.

Сила тренияявляется суммой сил

^где— сила трения на направляющих люльки, про­

порциональная нормальной составляющей веса (рис. 12.15); — сила трения в уплотнениях противооткатных устройств, которую принимают пропорцио­нальной весу откатных частей.

Тогда

гдеиимеют вышеуказанные числовые значения.

Обратим внимание, что формула (12.62) для определения силы трениясправедлива для любых углов возвышения ствола после подстановки в нее угла ср, при котором сила трения определяется. На практике

Величина силырассчитывается исходя из условия устой­

чивости орудия (12.13) с учетом того, что при

где— масса орудия в боевом положении.

Так как путь Х_х еще неизвестен, можно приниматьВторой период. Во втором периоде откатаТогда из формул перехода (12.51) после интегрирования следует, что

Расчет элементов отката ведется в тех же точках, что и для свободного отката. В конце второго периода

Тогда

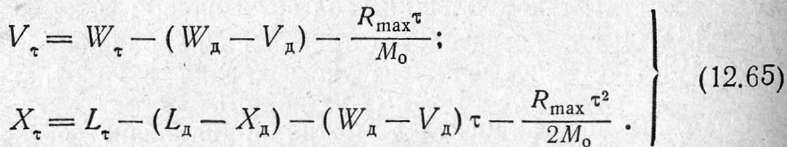
Второй период отката характерен тем, что в этом периоде ско­рость торможенного отката может достигать максимального значе­ния. Максимальноезначение скоростибудет соответствовать моменту временипри котором(рис. 12.16). При— откат будет ускоренным. При— откат замедленный. С точки зрения математики в момент вре­мени

Следовательно, производная, что соответствует экстре­

муму.

Скорость и путь торможенного отката в момент временипа основе зависимостей (12.64) будут равны:

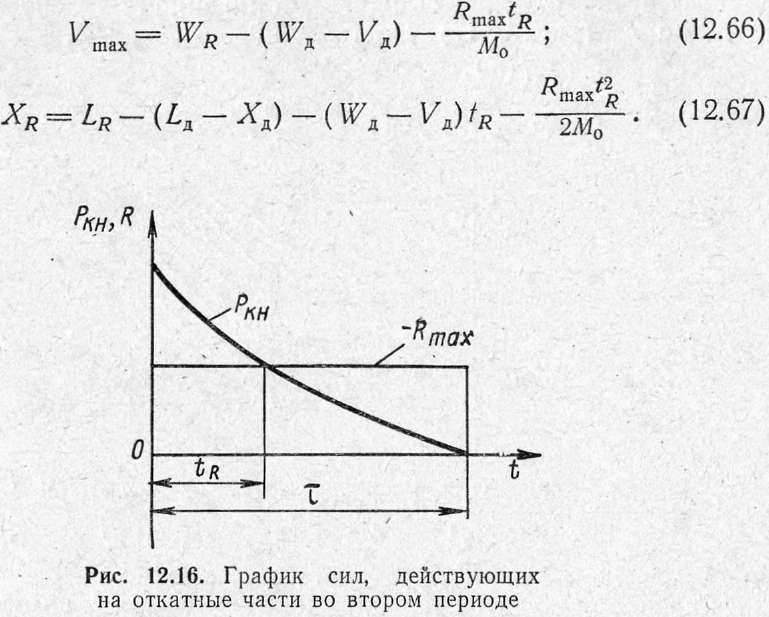
Для расчетанеобходимо знать времяТак как

при

то

Все вышесказанное о времени t_R справедливо при отсутствии дульного тормоза или при применении относительно малоэффек­тивных дульных тормозов, у которых импульсная характеристика %>0. При применении дульных тормозов с большой эффективно­стью с х<0, как отмечалось ранее, сила Ркндт в начале второго периода меняет свое направление (знак) и уравнение движения откатных частей будет иметь вид

Это означает, что сразу после вылета снаряда из канала ствола откат будет замедленным.

Следовательно, при применении дульных тормозов с импульс­ной характеристикоймаксимальная скорость отката будетсуществующих орудий

Третий период. В третьем периоде на откатные части дей­ствует только сила сопротивления откату R. При этомиз­меняется,как отмечалось ранее, по линейному закону от значениядо(рис. 12.17). Поэтому задача сводится к определению зависимости

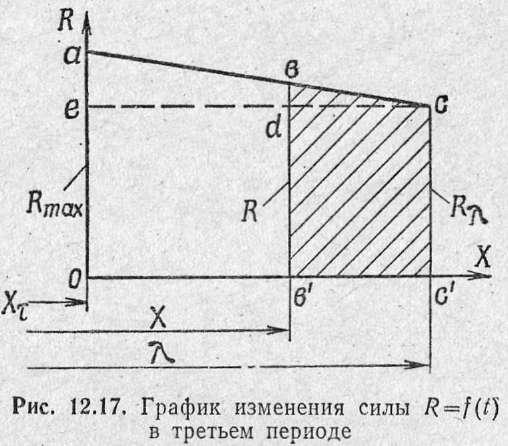
Вначале составим уравнение прямой, которое нам по­

надобится для определения скорости отката V. Из подобия тре­угольников (рис. 12.17) асе и bed следует

или

Отсюда

Скорость откатных частей найдем, применив к откатным ча­стям теорему об изменении кинетической энергии. Когда откатные части пройдут путь X, их скорость будет равна V. В конце откатаих скорость V=0.Работа силы R на путибудет равна пло­

щади трапецииСледовательно,

или

Подставляя в выражение (12.70) значение силы R (12.69), по­лучим квадрат скорости отката

Квадрат скорости определяется при расчетах через интервал путиОднако в формуле (12.71) неизвестна длина

откатгкоторую определяют, также применяя к откатным частям теорему об изменении кинетической энергии на пути.. При

,а приРабота силы R, затраченная на

изменений кинетической энергии, равна площади трапецииСледовательно,

откуда

Из условия устойчивости орудия и

Подставляя значенияв выражение (12.72) и пре­

образуя относительнополучаем

где

Очевидно, что

Продолжительность третьего периодаопределяем из уравне­ния изменения количества движения откатных частей:

где

Отсюда продолжительность третьего периода

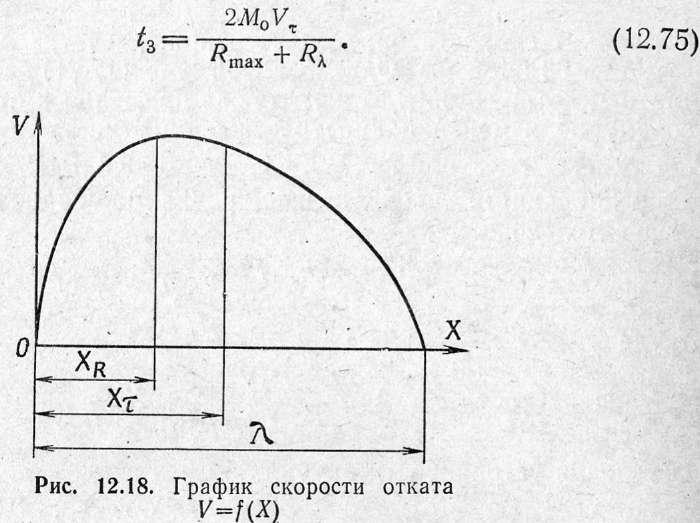
Полное время отката

В заключение приведем примерный график изменения скорости откатных частей при выстреле (рис. 12.18).