
- •§ 1. Принцип устройства и действия орудия
- •§ 2. Основные характеристики орудия
- •§ 3. Классификация и требования, предъявляемые к артиллерийским орудиям
- •§ 4. История развития советской артиллерии
- •Раздел I
- •Глава 1
- •§ 1.1. Явление выстрела
- •§ 1.2. Параметры внутренней баллистики
- •§ 1.3. Горение пороха
- •§ 1.4. Образование пороховых газов
- •§ 1.5. Давление пороховых газов в постоянном объеме
- •§ 2.1. Расширение пороховых газов
- •§ 2.2. Движение снаряда в канале ствола
- •§ 2.3. Работы, совершаемые пороховыми газами
- •§ 2.4. Последействие пороховых газов
- •Глава 3
- •§ 3.1. Система уравнений внутренней баллистики
- •§ 3.2. Решение основной задачи
- •§ 3.3. Таблицы внутренней баллистики
- •§ 3.4. Поправочные формулы внутренней баллистики
- •Глава 4
- •§ 4.1. Назначение боеприпасов и требования, предъявляемые к ним
- •§ 4.2. Принципы устройства выстрелов
- •§ 4.3. Комплектация выстрелов
- •§ 4.4. Окраска и маркировка боеприпасов
- •Глава 5
- •§ 5.1. Силы, действующие при выстреле
- •§ 5.2. Силы, действующие в полете
- •§ 6.1. Конструкция и характеристики снарядов
- •§ 6.2. Ударное действие снарядов
- •§ 6.3. Осколочное действие снарядов
- •§ 6.4. Фугасное действие снарядов
- •§ 6.5. Действие кумулятивных снарядов
- •§ 6.6. Действие снарядов специального назначения
- •§ 7.1. Ударные взрыватели
- •§ 7.2. Дистанционные и неконтактные взрыватели
- •§ 7.3. Действие взрывателей
- •§ 7.4. Условия безопасности и взводимости взрывателей
- •Глава 8 боевые заряды
- •§ 8.1. Пороховые заряды
- •§ 8.2. Гильзы
- •§ 8.3. Средства воспламенения
- •Глава 9
- •§ 9.1. Хранение и сбережение боеприпасов
- •§ 9.2. Эксплуатация боеприпасов на огневой позиции
- •Глава 10 орудийные стволы
- •§ 10.1. Типы и конструкция стволов
- •§ 10.2. Силы, действующие на ствол при выстреле
- •§ 10.3. Предел упругого сопротивления ствола-моноблока
- •§ 10.4. Расчет ствола-моноблока на прочность
- •Глава 11 затворы § 11.1. Типы и конструкции затворов
- •§ 11.2. Запирающие механизмы
- •§ 11.3. Ударные и спусковые механизмы
- •§ 11.4. Выбрасывающие механизмы
- •§ 11.5. Полуавтоматика
- •§ 11.6. Предохранительные и вспомогательные механизмы
- •§ 11.7. Эксплуатация затворов
- •Глава 12
- •§ 12.2. Свободный откат ствола
- •§ 12.3. Дульный тормоз и его влияние на откат ствола
- •§ 12.4. Торможенный откат
- •§ 12.5. Устойчивость и неподвижность орудия при накате
- •Глава 13 противооткатные устройства
- •§ 13.1. Накатники
- •§ 13.2. Гидравлические тормоза отката
- •§ 13.3. Накат ствола
- •§ 13.4. Основы эксплуатации противооткатных устройств
- •I. Расчет свободного отката а. Первый период
- •Б. Второй период
- •III. Расчет накатника
- •3. Сила накатника для рассчитанных значений длины отката ( табл. 2 )
- •IV. Расчет тормоза отката веретенного типа а. Расчет тормоза отката
- •12; Величина (табл. 3)
- •Глава 14
- •§ 14.1. Уравновешивающие механизмы
- •§ 14.2. Механизмы наведения
- •§ 14.3. Электрические приводы
- •§ 14.4. Эксплуатация механизмов
- •Глава 15
- •§ 15.1. Лафеты
- •§ 15.2. Ход и подрессоривание
- •§ 15.3. Вспомогательное оборудование
- •Глава 16
- •§ 16.1. Типы прицелов и требования, предъявляемые к ним
- •§ 16.2. Механические прицелы
- •§ 16.3. Оптические прицелы и визиры
- •§ 16.4. Ночные прицелы
- •§ 16.5. Эксплуатация прицелов
- •Глава 17
- •§ 17.2. Особенности устройства артиллерийской части самоходных орудий
- •§ 17.3. Действие выстрела на самоходное орудие
- •Глава 18
- •§ 18.1. Порядок разработки орудий
- •§ 18.2. Испытания орудий
- •Глава 19
- •§ 19.1. Организация эксплуатации
- •§ 19.2. Осмотры и технические обслуживания
- •§ 19.3. Хранение и сбережение
- •§ 1. Принцип устройства и действия орудия . .* —
§ 10.3. Предел упругого сопротивления ствола-моноблока
Для сообщения снаряду требуемой скорости в канале ствола создается довольно высокое давление газов, которое стремится не только переместить снаряд, но и разрушить ствол. Чтобы ствол выдерживал это давление, не разрушаясь в течение всего срока его эксплуатации, он должен быть достаточно прочным. Мерой прочности является предел упругого сопротивления ствола.
Пределом упругого сопротивления ствола называется такое максимальное давление газов в канале, при котором в стенках ствола не образуются остаточные деформации.
При определении величины предела упругого сопротивления ствола используют одну из четырех существующих в настоящее время теорий прочности, каждая из которых по-разному подходит
к моменту появления остаточных деформаций в металле, подвер- j женному объемному напряженному состоянию.
В
Советском Союзе и в ряде государств
Европы применяют вторую теорию прочности
при определении предела упругого со- i
противления ствола. Согласно этой теории
остаточные деформации в материале,
подверженном объемному напряженному
состоянию, наступают тогда, когда
наибольшее относительное удлинение
бу- : дет больше относительного удлинения
при простом растяжении
в момент
достижения в материале напряжения,
равного пределу упругости. Поэтому в
зависимости от того, что в каждом конкрет-
. ном случаебольше относительные
тангенциальные (окружные) удлинения![]() или
относительные радиальные удлинения
или
относительные радиальные удлинения![]() условие
прочности по этой теории будет
соответственно выглядеть так:
условие
прочности по этой теории будет
соответственно выглядеть так:
![]()
или
![]()
где![]() —
модуль упругости первого рода;
—
модуль упругости первого рода;![]() —
предел упругости.
—
предел упругости.
Основываясь на условии (10.25) или (10.26), определяют предел упругого сопротивления ствола. Предварительно устанавливают зависимости между главными напряжениями и деформациями, возникающими в стенках ствола при выстреле.
Установление этих зависимостей проводят при следующих допущениях:
труба имеет цилиндрическую форму до и после деформации, и всякое сечение, плоское до деформации, остается плоским и после деформации;
материал трубы однороден и изотропен;
по поверхностям трубы силы давления распределены равномерно и приложены нормально к ним;
частицы металла под действием внешних сил находятся в равновесии.
В общем случае стенки ствола при выстреле под действием сил давления пороховых газов подвергаются сложному нагружению и испытывают объемные деформации. В его поперечных сечениях происходит растяжение металла по окружностям, имеющим центр на оси канала, и одновременно сжатие по радиальным направлениям. Кроме того, под действием сил инерции ствола и силы продольного давления ведущего пояска на нарезы, направленных вперед, возникает осевое растяжение в продольном сечении ствола.
Для
определения напряжений в стенке ствола,
возникающих под действием давления
газов, выделяют из него концентрическими
поверхностями с радиусами![]() бесконечно
малый элемент длиной
бесконечно
малый элемент длиной![]() с
центральным углом
с
центральным углом![]() .
отстоящий от казенного среза на
расстоянии
.
отстоящий от казенного среза на
расстоянии![]() (рис.
10.15,а).
(рис.
10.15,а).
Пусть
на внутренней поверхности этого элемента
возникают радиальные напряжения![]() на
наружной—
на
наружной—![]() на
торцевых
на
торцевых
поверхностях
— окружные напряжения![]() а
на поверхностях, перпендикулярных
плоскости чертежа, — осевые напряжения
а
на поверхностях, перпендикулярных
плоскости чертежа, — осевые напряжения![]() и
и
![]()
а —
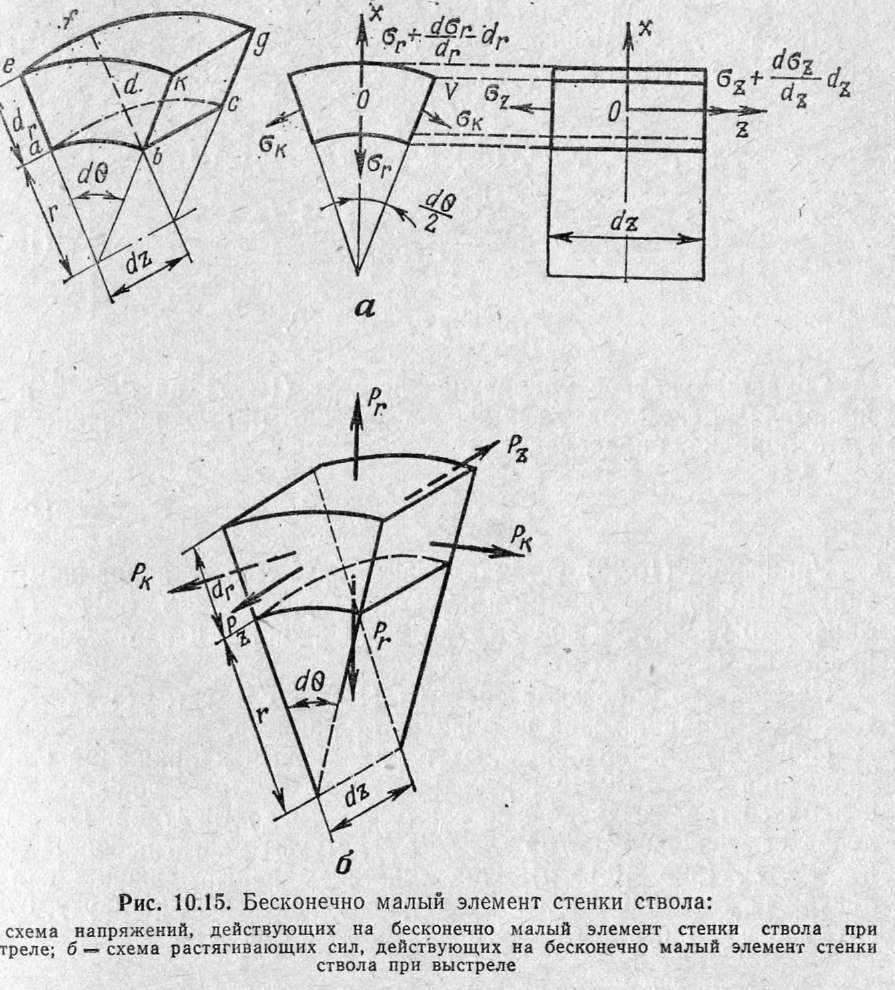
Согласно
допущениям элемент при деформации
перекашиваться не будет, а следовательно,
касательные напряжения по его граням
будут отсутствовать. Значит, по
поверхностям этого элемента действуют
внутренние силы, равнодействующие
которых приложены к центру граней и
равны произведению напряжения на
соответствующую площадь грани, т. е.
равнодействующая сила внутренней
поверхности равна![]() наружной
поверхности —
наружной
поверхности —
![]()
![]()
![]() боковых
поверхностей —
боковых
поверхностей —![]() торце
торце
вых
—![]() и
и![]()
На
основании допущения, что частицы
материала трубы под действием внешних
сил находятся в равновесии, используя
уравнение статики, приравнивают нулю
сумму проекций сил, действующих на
элемент, на каждую из трех взаимно
перпендикулярных осей![]() Ось
Ось![]() направлена
по радиусу ствола, ось
направлена
по радиусу ствола, ось![]() —по
оси
—по
оси
ствола,
а ось
Y
перпендикулярна осям![]()
Проектируя
силы на ось![]() и
учитывая, что ввиду мало
и
учитывая, что ввиду мало
сти
угла![]() получают
получают

Сокращая
первое уравнение системы (10.27) на![]() и
от
и
от
брасывая члены, содержащие бесконечно малые величины высшего порядка, определяют
![]()
Уравнение (10.28) устанавливает связь между радиальными и окружными напряжениями и называется уравнением Ляме — Гадо- лина. Это уравнение показывает, что окружные и радиальные напряжения не зависят от осевых.
Из третьего уравнения системы (10.27) следует, что cz = const, т. е. осевые напряжения не зависят от радиуса.
При определении окружных и радиальных напряжений одного уравнения системы (10.28) недостаточно, поэтому дополнительно к нему составляют условные совместности деформаций. На выделенный бесконечно малый элемент действуют растягивающие силы
![]() (рис.
10.15,6). Под действием растягивающих сил
(рис.
10.15,6). Под действием растягивающих сил![]() линейный размер элемента будет
увеличиваться по радиусу, относительное
удлинение которого
линейный размер элемента будет
увеличиваться по радиусу, относительное
удлинение которого
![]()
В
то же время от действия сил![]() линейныйразмер
эле
линейныйразмер
эле
мента
будет уменьшаться в направлении
радиуса![]() При
этом относительное укорочение
При
этом относительное укорочение
![]()
где![]() —коэффициент
Пуассона (для стали
—коэффициент
Пуассона (для стали![]() ).
).
Следовательно,
полная относительная деформация элемента
в направлении радиуса![]() выразится
разностью относительного удлинения
и укорочения, т. е.
выразится
разностью относительного удлинения
и укорочения, т. е.
![]()
Подобные
выражения получают и для относительных
деформаций в направлении действия
сил![]() т.
е.
т.
е.

Принимая
во внимание допущение о том, что всякое
сечение после деформации остается
плоским, т. е. относительная осевая
деформация![]() не
зависит от радиуса, устанавливают, что
не
зависит от радиуса, устанавливают, что
![]()
Дифференцируют
выражение (10.31) по![]() и
с учетом зависимости (10.32) получают
и
с учетом зависимости (10.32) получают
![]()
Следовательно
![]()
Подставляя
в формулу (10.34) значение![]() из
зависимости (10.28), находят
из
зависимости (10.28), находят
![]()
Умножая
обе части выражения (10.35) на
rdr,
имеют
![]() или
или
![]()
Интегрируя
последние выражения, получают
![]() откуда
откуда
![]()
Подставляя
в уравнение (10.34) значениеиз
зависимости X 10.36), определяют![]()
![]()
Постоянные
интегрирования![]() находят
из граничных усло
находят
из граничных усло
вий на внутренней и наружной поверхностях цилиндра:
![]()
Знак
«минус» в правых частях этих формул
говорит о том, что положительными
радиальными напряжениями![]() приняты
растягивающие напряжения (рис.
10.15,6). Подставляя граничные условия
(10.38) при соответствующих
приняты
растягивающие напряжения (рис.
10.15,6). Подставляя граничные условия
(10.38) при соответствующих![]() в
выражение (10.36), получают
в
выражение (10.36), получают

Решая
совместно уравнения (10.39) и (10.40)
относительно![]() и
и![]() определяют
определяют

Подставляя
значения![]() в
выражения (10.36) и (10.37), на
в
выражения (10.36) и (10.37), на
ходят

Приближенно
осевые напряжения в стенках ствола
могут быть определены так:![]()
где![]() —осевые
напряжения, возникающие от силы
продольного давления ведущего пояска
на боевую грань нареза; определяются
по формуле
—осевые
напряжения, возникающие от силы
продольного давления ведущего пояска
на боевую грань нареза; определяются
по формуле
![]()
—
осевые
напряжения, возникающие от силы инерции
![]() ствола
при выстреле; определяются по формуле
ствола
при выстреле; определяются по формуле![]()
![]() —осевые
напряжения в стенках каморы, возникающие
от действия силы
—осевые
напряжения в стенках каморы, возникающие
от действия силы![]() определяются
по формуле
определяются
по формуле
![]()
где![]() —
длина каморы;
—
длина каморы;
![]() —расстояние
до рассматриваемого сечения.
—расстояние
до рассматриваемого сечения.

Формулы (10.46), (10.47) и (10.48) применяют для определения нормальных осевых напряжений в стенках ствола.
Анализ
вида эпюр (рис. 10.16) радиальных, окружных
и осевых нормальных напряжений в
поперечном сечении ствола, рассчитанных
по формулам (10.43), (10.44) и (10.45) при![]()
![]() показывает
следующее:
показывает
следующее:
Для любого радиуса г абсолютные величины окружных напряжений больше абсолютной величины радиальных напряжений, т. е.

Наибольшее напряжение возникает на внутренней поверхности трубы. Следовательно, при чрезмерно высоком давлении рх первоочередному разрушению подвержены внутренние слои металла трубы.
Зависимости (10.29), (10,30), (10.31) приводят к следующему
виду:
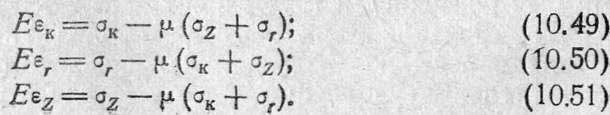
Произведения![]() называются
соответственно приведен
называются
соответственно приведен
ными окружными, радиальнымии осевыми напряжениями.
Подставляют
значения![]() и
и![]() из
уравнений (10.43), (10.44) и
из
уравнений (10.43), (10.44) и
/
![]() в
формулы (10.49), (10.50) и (10.51), которые после
несложных преобразований принимают
следующий вид:
в
формулы (10.49), (10.50) и (10.51), которые после
несложных преобразований принимают
следующий вид:

Из
анализа уравнений (10.52), (10.53), (10.54) и вида
эпюр приведенных напряжений (рис.
10.17), вычисленных по этим уравнениям
при![]() устанавливают
следующее:
устанавливают
следующее:
В поперечном сечении приведенные окружные напряжения по абсолютной величине всегда больше радиальных и осевых для одного значения текущего радиуса

Наибольшие приведенные напряжения возникают на внутренней поверхности трубы при

На
основании этих выводов предел упругого
сопротивления ■ ствола определяют из
условия прочности (10.25) для окружных
относительных удлинений![]() Подставляя
в условие (10.25) значе
ние
sK
из
формулы (10.52), полагая при этом
Подставляя
в условие (10.25) значе
ние
sK
из
формулы (10.52), полагая при этом![]() после несложных преобразований получают
после несложных преобразований получают
![]()

Из зависимости (10.55) определяют предел упругого сопротивления ствола
![]()
Анализ
формулы показывает, что предел упругого
сопротивле« ния ствола![]() зависит
от качества материала ае
и толщины стенки ствола
зависит
от качества материала ае
и толщины стенки ствола![]()
Обычно
стволы изготовляют из специальных
орудийных сталей с![]() Калибр
ствола — величина заданная, значит,
повышение предела упругого сопротивления
Калибр
ствола — величина заданная, значит,
повышение предела упругого сопротивления![]() при
определенномкачестве материала
достигается увеличением наружного
радиуса
при
определенномкачестве материала
достигается увеличением наружного
радиуса![]() Целесообразный
интервал увеличения радиуса
Целесообразный
интервал увеличения радиуса![]() устанавливают
из зависимости (10.56) при
устанавливают
из зависимости (10.56) при![]() Для
определения вида этой зависимости делят
числитель и знаменатель формулы (10.56)
на
Для
определения вида этой зависимости делят
числитель и знаменатель формулы (10.56)
на![]() и
после несложных преобразований получают
и
после несложных преобразований получают
![]()
Таким
образом, зависимость (10.57) показывает,
что при бесконечном увеличении
толщины стенок ствола предел упругого
сопротивления ствола стремится к
величине![]()
Анализ графика зависимости предела упругого сопротивления и массы ствола от толщины стенок (рис. 10.18) позволяет сделать
вывод,
что толщину стенок по сечению
нецелесообразно делать свыше (0,8—1)![]() так
как при дальнейшем ее увеличении незна-
• чительно повышается предел упругого
сопротивления и резко воз-
J
растает
масса ствола.
так
как при дальнейшем ее увеличении незна-
• чительно повышается предел упругого
сопротивления и резко воз-
J
растает
масса ствола.
У
большинствасуществующих орудий толщина
стенок ствола примерно равна![]() (так,
например, ствол 76-мм пушки ЗИС-З
(так,
например, ствол 76-мм пушки ЗИС-З
имеет
толщину стенки в месте максимального
давления А = 35 мм, а ствол 152-мм гаубицы-пушки
MJI-20
имеет![]() ).
).
