6. Плоская гармоническая волна в проводящей среде

Пусть плоская гармоническая волна проникает в проводящую среду ) через плоскость, нормальную и направленную движе­ния волны.

Система уравнений Максвелла в комплексной форме будет иметь вид:

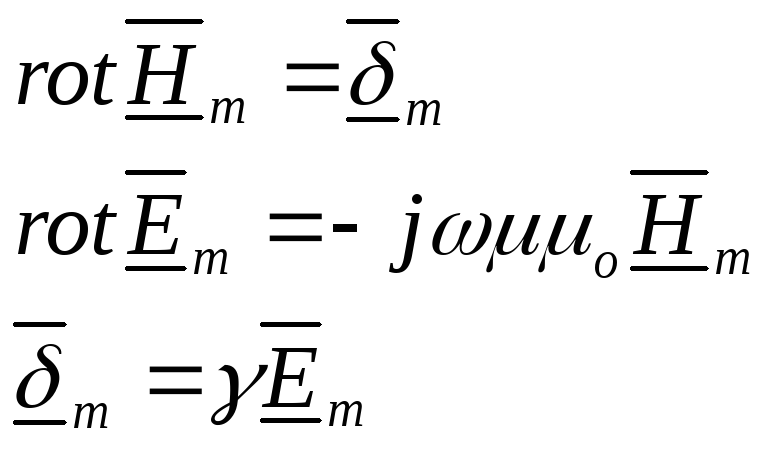
Плотностью тока смещения () в уравнении (1) пренебрегаем в связи с ее малостью по сравнению с плотностью тока проводимости.

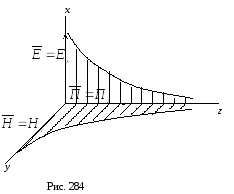
Выберем направления осей координат так, чтобы вектор сопадал с осьюx (), векторсовпадал с осьюy (), тогда вектор Пойтингабудет направлен по осиz () (рис. 284). При таком выборе направле­ний осей координати система уравнений Максвелла получит вид:

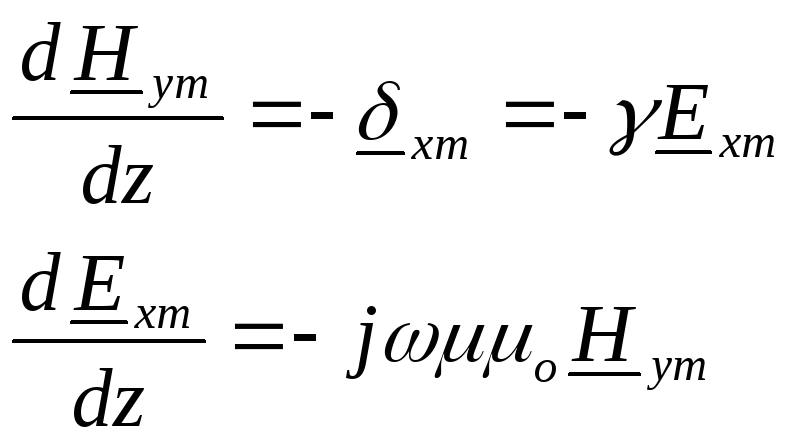
Решим данную систему дифференциальных уравнений относительно од­ной из пере­менных, например, . Для этой цели продифференцируем уравнение (2) по пере­менной (z) и сделаем в него подстановку из уравнения (1):

Введем обозначения:

, где .

С учетом принятых обозначений дифференциальное уравнение получит стандартную форму:

.

Решение дифференциального уравнения:

,

где ₁= p = b – jb, ₂ = b+jb  корни характеристического уравнения.

Если среда распространения волны не ограничена, то отраженная волна отсутствует и второе слагаемое из решения можно исключить, тогда решение в комплексной форме по­лучит вид:

Перейдем от комплексного изображения к функции времени:

Решение для волны в комплексной форме получим из уравнения (2) путем подстановки в него найденного решения для:

,

где 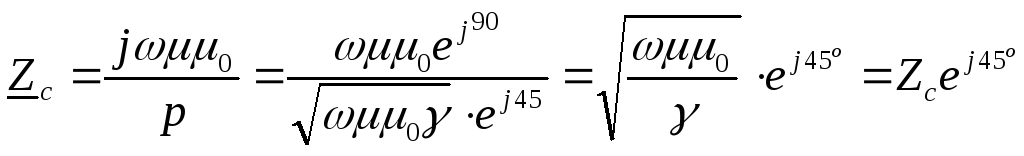комплексное волно­вое сопро­тивле­ние среды, которое носит активно-индуктивный характер.

Перейдем от комплексного изображения к функции времени:

Таким образом, электромагнитное поле в проводящей среде распростра­няется в виде затухающих взаимно перпендикулярных волн и. Множительпоказывает, что амплитуды волн при своем перемещении зату­хают по экспоненциальному закону. Глу­биной проникновения поля называется расстояние, на котором амплитуды волн затухают враза, т.е, от­куда.

Фазовая скорость определяется из условия, что , откуда следует, что.

Длина волны  равна расстоянию, на котором фаза волны изменяется на 2, т. е. , откуда. На расстоянии длины волныz = зату­хание волны составит раз.

7. Поверхностный эффект в плоском листе

Ранее было показано, что переменное электромагнитное поле быстро за­тухает по мере проникновения в толщу проводящей среды. Это приводит к не­равномерному распреде­лению поля по сечению магнитопровода, и следова­тельно, к неравномерному распределе­нию магнитного потока по сечению: на оси магнитопровода плотность магнитного потока наименьшая, а у поверхно­стного  наибольшая.

Для более равномерного распределения магнитного потока по сечению магнитопро­вода и для уменьшения потерь на вихревые токи, магнитопроводы трансформаторов соби­раются из отдельных тонких листов электротехнической стали, изолированных друг от друга. Исследуем распространение переменного поля в таком листе.

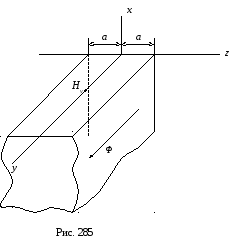
Пусть в плоском листе толщиной , высотойh и длинной l направление маг­нитного потока Ф и, следовательно, векторов поля совпадают с осьюу (рис. 285):

На основании предыдущего параграфа решения для вектора будет иметь вид:, где.

Поле проникает в пластину с двух сторон, а на поверхности пластины с обеих сторон при векторы поля должны быть равны, следовательно:

,

тогда решение для произвольной точки:

.

Амплитуда магнитного потока Ф_m и среднее значение амплитуды индук­ции магнит­ного поля определяются согласно уравнению трансформатор­ной ЭДС.

.

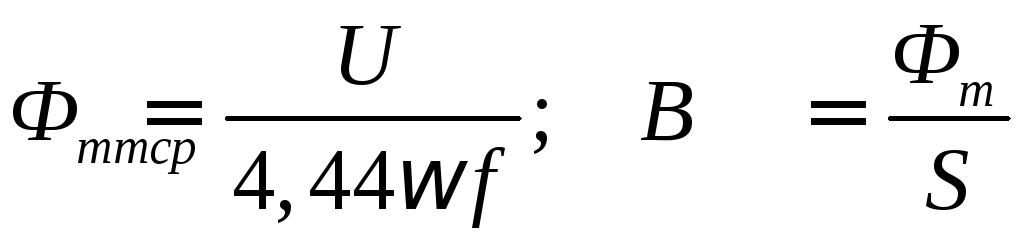Выразим из уравнения распределенияпо сечению листа:

,

откуда следует, что, т. е амплитуда индукции у поверхности листа пре­вышает ее среднее значение.

Распределение магнитного поля по сечению листа в зависимости от его толщины d при частоте f=100 Гц показано на рис. 286.